01 多项式 | 高等代数
1. 数域
- 数域P定义:
- 包括0和1
- 任意两个数的和差积商(除数不为零)都落在P
- 有理数域是任意数域P的一部分
2. 一元多项式
- 一元多项式定义:
- 次数n为非负整数
- 有限项
- 系数属于数域P,这些一元多项式的全体为数域P上的一元多项式环,记作
- 多项式分类
- 系数全为0为零多项式,不定义次数
- 当同次项的系数全部相等,则多项式相等
- 次数
- 多项式乘法
- 如果
- 则
- 如果
环和域
环对除法不封闭:两个典型的整环:整数环和一元多项式环
域对四则运算封闭:例如有理数域和有理式域
3.整除的概念
- 带余除法:对于
- 整除:如果数域P上存在
- 整除
- 当
- 如果
- 整除具有传递性:
- 组合:如果
- 两个多项式之间的整除关系不会因为系数域的扩大而改变
- 整除
4. 最大公因式
1. 最大公因式的定义
假设
我们用
2. 一元多项式的贝祖定理
- 对于
- 带余除法引理:若
- 辗转相除法:假设
则不断往回代得: - 求解最大公因式的方法:辗转相除法+竖式除法:

3. 多项式的互素
- 互素:两个多项式
- 互素的充要条件: 存在多项式
- 互素的性质定理
- 如果
- 如果
- 如果
4. 多个多项式的最大公因式
- 定义:
- 如果存在
5. 因式分解定理
1. 不可约多项式
- 不可约多项式的定义:数域
- 是否可约依赖于数域的选择
- 不可约多项式的性质
- 一次多项式总是不可约多项式
- 不可约多项式的因式只有非零常数和
- 零多项式和零次多项式无可不可约的说法(次数必须大于等于
- 不可约多项式的等价描述
- 由
2. 因式分解唯一性
-
因式分解及唯一性定理:数域
-
-
标准分解式:
-
若次数大于等于1的多项式
其中
6. 重因式
- 重因式定义:不可约多项式
- 重因式定理
- 重因式定理:如果不可约多项式
- 逆定理:
- 推论
- 如果不可约多项式
- 重因式的 判断 :不可约多项式
- 多项式
- 判断多项式是否是重因式可以 求导+辗转相除法
- 如果不可约多项式
- 去除因式重数的方法:
- 重因式定理:如果不可约多项式
7. 多项式函数
1. 多项式函数
- 多项式函数定义:设
- 上述的
- 余数定理 : 用多项式
- 重根:如果
- 若
2. 多项式函数定理
- 如果
3.
- 设
8. 复系数与实系数多项式的因式分解
-
代数基本定理
- 代数基本定理:每一个次数
- 每一个次数
- 复数域上次数
- 代数基本定理:每一个次数
-
多项式 根 复平面旋转角度 -
复系数多项式因式分解定理: 每个次数
-
实系数多项式因式分解定理: 每个次数
9. 有理系数多项式
1. 本原多项式
- 本原多项式定义:如果一个非零整系数多项式的系数都是 互素 的,那么就称为 本原多项式
- 任意有理系数多项式都可以表示为一个有理数乘上一个本原多项式
- 高斯引理:任何两个本原多项式的 乘积 还是本原多项式
- 非零整系数多项式
- 推论:设
- 一个次数大于零的本原多项式
- 推论:设
2. 有理根
- 设
- 爱森斯坦
- 如果存在 素数
则
- 如果存在 素数
则
- 如果存在 素数
__EOF__
本文作者:RadiumGalaxy
本文链接:https://www.cnblogs.com/RadiumGalaxy/p/16759778.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!
本文链接:https://www.cnblogs.com/RadiumGalaxy/p/16759778.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!
分类:
Advanced Algebra
标签:
Courses



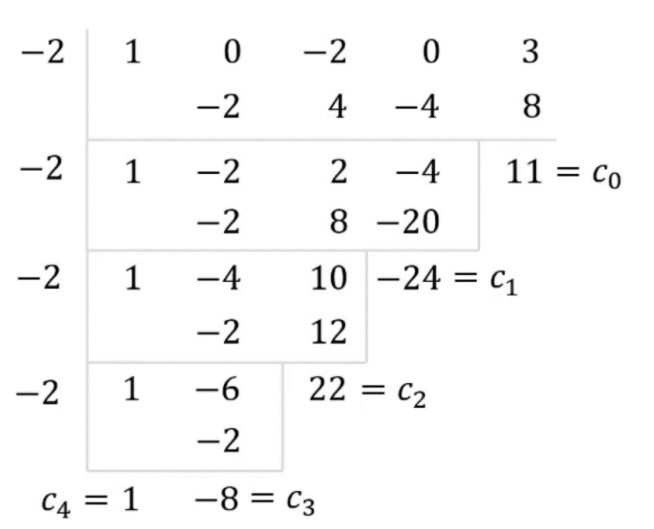
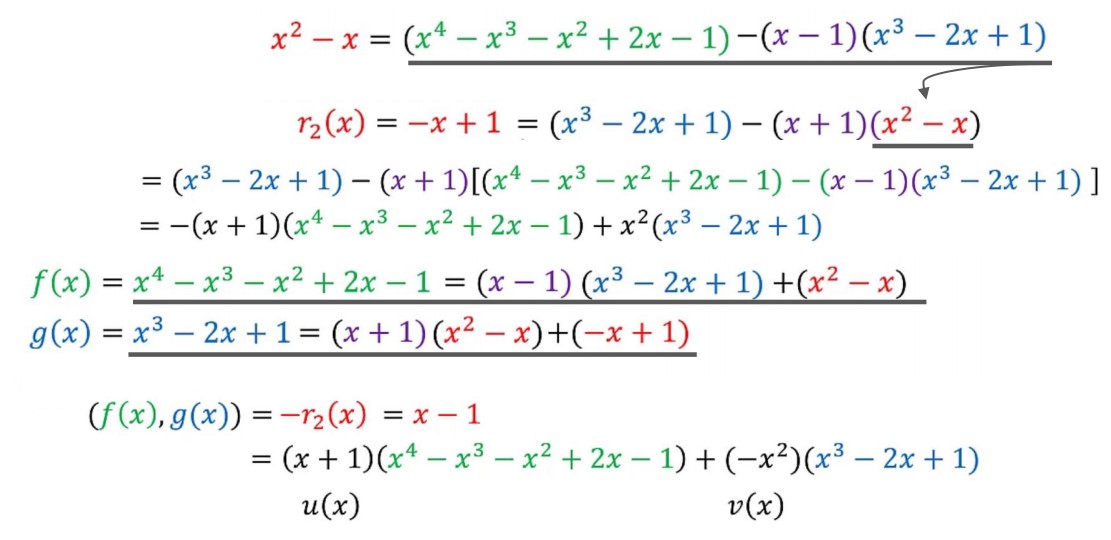



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 一文读懂知识蒸馏
· 终于写完轮子一部分:tcp代理 了,记录一下