浅谈树状数组
P.S. 树状数组之前认为难以理解,但是看了这个之后,恍然大悟,以下题目来自洛谷
先三连+%up为敬
问题P3374:给你n个数,要进行k次单点修改和区间查询的操作
给出一个表来对比一下暴力和树状数组:
| 做法 | 修改复杂度 | 查询复杂度 |
|---|---|---|
| 朴素暴力 | \(O(1)\) | \(O(n×k)\) |
| 树状数组 | \(O(logn)\) | \(O(logn)\) |
借百度的图讲一下:
令这棵树的结点编号为\(f_1\),\(f_2\)...\(f_n\),数组编号为\(a_1\),\(a_2\)...\(a_n\)
所以:
\(f_1\)=\(a_1\)
\(f_2\)=\(a_1\)+\(a_2\)
\(f_3\)=\(a_3\)
\(f_4\)=\(a_1\)+\(a_2\)+\(a_3\)+\(a_4\)
……
发现性质:设节点编号为\(i\),那么这个节点管辖的区间为\(2^k\)(其中\(k\)为\(i\)二进制末尾0的个数)个元素
因为这个区间最后一个元素必然为\(a_i\),
比如说,我们要求\(f_4\),可以得到
\(f_4\)=\(a_1\)+\(a_2\)+\(a_3\)
把4转换为2进制,\((4)_{10}\)=\((100)_2\)
然后就是区间查询
假如我们要查询\(a_1\)+\(a_2\)+...+\(a_{13}\)的值就是要查询这几个区间的和的:
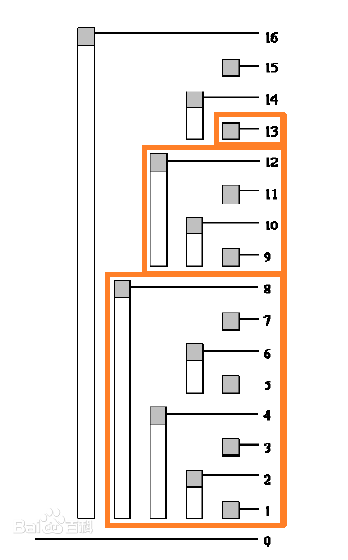
所以\(a_1\)+\(a_2\)+...+\(a_{13}\)=\(f_8\)+\(f_{12}\)+\(f_{13}\),只用把3个值加起来就行了
\((13)_{10}\)=\((1101)_2\)
| 操作 | 1 | 2 | 3 |
|---|---|---|---|
| 抹去二进制的最后一个1 | \((1101)_2\) | \((1100)_2\) | \((1000)_2\) |
| 转化成十进制 | 13 | 12 | 8 |
| 管辖的范围 | \(2^0\) | \(2^2\) | \(2^3\) |
神奇的发现:\(2^0\)+\(2^2\)+\(2^3\)恰好等于13



由于每次最多抹掉\(log(n)\)个0,也就是最多有\(log(n)\)次查询,复杂度为\(O(logn)\)
接下来是单点修改
假如要修改的节点编号为\(i\)
由于\(f\)数组储存的是前缀和,所以要修改所有包含\(i\)的区间
当\(i\)=5时,就是要修改这几个区间的值:
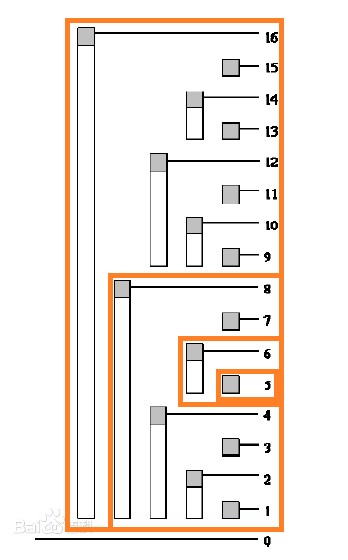
不难发现,对于单点修改的操作,其实就是把区间查询的操作倒了过来
| 操作 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 在二进制的最后一个1的位置加1 | \((101)_2\) | \((110)_2\) | \((1000)_2\) | \((10000)_2\) |
| 转化成十进制 | 5 | 6 | 8 | 16 |
| 管辖的范围 | \(2^0\) | \(2^1\) | \(2^3\) | \(2^4\) |
这里就不再阐述了
总结:查询就是在最后一个1的位置减1,修改就是在最后一个1的位置加1
那怎么得到二进制的最后一个1在哪里
\(\large\boxed{lowbit}\)操作
inline int lowbit(int x) { return x & -x; }
这段代码是什么含义呢?
先谈谈二进制中如何表示负数:
一个正数的相反数用二进制表示就是这个数按位取反再+1
比如说\((1100)_2\)的负数用二进制表示就是\((0011)_2\)+1,也就是\((0100)_2\)
\(1100\)&\(0100\)=\(0100\)
那为什么\(lowbit\)能求二进制最末位的1在哪?
我们要求的这个数末尾连续的0取反之后会全部变成1(就是二进制下这个数的相反数减一之后末尾的1与这个数末尾的0的数量相同)
在负数中把减去的1加上之后,末尾的1会全部变成0,而最末尾的0会变成1(加法)
以12为例子,给张图理解一下:

放上核心代码:
int n, f[100003];
inline int lowbit(int x) { return x & -x; }
inline int query(int x)//查询
{
int ans = 0;
while (x)
ans += f[x], x -= lowbit(x);
return ans;
}
inline void add(int x, int val)//修改
{
while (x <= n)
f[x] += val, x += lowbit(x);
}
P.S.求\([l,r]\)区间和就是求\(query(r)-query(l-1)\)的值
问题P3368区间修改和单点查询
如果上面宁已经看懂了,接下来的内容就很简单了
区间修改,其实用到了差分的思想
之前的\(f_i\)是指\(1\)~\(i\)的和(及前缀和),这里\(f\)储存的是差分数组
还是拿百度的图举例子
假如此时我们要把区间\(a[1,6]\)都加上值\(val\)应该如何操作呢?

利用差分的思想,在1的位置上加上val,在6+1的位置上减去val
这样查询\(f[1,6]\)时,就正好加上了值,查询到大于6的时候,先加了\(val\),又减去了\(val\)正好抵消\(qwq\)
然后给出\(\color{limegreen}{AC}\)代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m,opt,l,r,k,pre,now,f[500005];
inline ll read(){
ll x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
inline ll lowbit(ll x){return x&-x;}
inline ll query(ll x){ll ans=0;while(x) ans+=f[x],x-=lowbit(x);return ans;}
inline void add(ll x,ll val){while(x<=n) f[x]+=val,x+=lowbit(x);}
int main(){
n=read(),m=read();
for(ll i=1;i<=n;++i){now=read();add(i,now-pre);pre=now;}
while(m--){
opt=read();
if(opt==1) {l=read(),r=read(),k=read();add(l,k),add(r+1,-k);}
else k=read(),printf("%lld\n",query(k));
}
return 0;
}
欢迎提出建议\(qwq\)
完结撒花\(qwq\)


