ZOJ 1081 Within（点是否在多边形内）| 计算几何

ZOJ 1081 Within

我使用的是“射线法”：从该点出发，作一条向左的水平射线，与多边形的边的交点有奇数个则点在多边形内。

需要注意的点：

1. 如果点在多边形的边上特判。
2. 考虑射线与多边形的一个交点是多边形的顶点的情况，
   
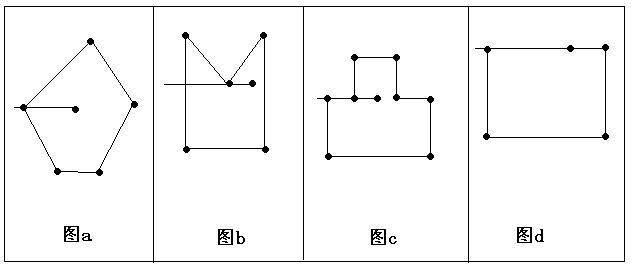
   最左边的那个顶点算一个交点，左边第二种的那个顶点算两个交点或不算交点都行（但不能算一个交点）。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
template <class T>
void read(T &x){
    char c;
    bool op = 0;
    while(c = getchar(), c < '0' || c > '9')
	if(c == '-') op = 1;
    x = c - '0';
    while(c = getchar(), c >= '0' && c <= '9')
	x = x * 10 + c - '0';
    if(op) x = -x;
}
template <class T>
void write(T x){
    if(x < 0) putchar('-'), x = -x;
    if(x >= 10) write(x / 10);
    putchar('0' + x % 10);
}
const int N = 105;
int n, m;
struct point {
    int x, y;
    point(){}
    point(int _x, int _y): x(_x), y(_y){}
    point operator - (point b){
	return point(x - b.x, y - b.y);
    }
    int operator * (point b){ // 这是叉乘
	return x * b.y - y * b.x;
    }
    int operator % (point b){ // 这是点乘
	return x * b.x + y * b.y;
    }
};
bool bel(point p, point u, point v){
    if((u - p) * (v - p)) return 0;
    return (u - p) % (v - p) <= 0;
}
struct poly {
    point p[N];
    bool includ(point q){
	int cnt = 0;
	for(int i = 1; i <= n; i++){
	    if(bel(q, p[i], p[i + 1])) return 1;
	    int d1 = q.y - p[i].y, d2 = q.y - p[i + 1].y;
	    int det = (p[i] - q) * (p[i + 1] - q);
	    if((det >= 0 && d1 < 0 && d2 >= 0) ||
	       (det <= 0 && d2 < 0 && d1 >= 0)) cnt++;
	}
	return cnt & 1;
    }
} P;
int main(){
    int T = 0, u, v;
    while(read(n), n){
	if(T) puts("");
	printf("Problem %d:\n", ++T);
	read(m), read(u), read(v);
	P.p[1] = P.p[n + 1] = (point){u, v};
	for(int i = 2; i <= n; i++){
	    read(u), read(v);
	    P.p[i] = (point){u, v};
	}
	while(m--){
	    read(u), read(v);
	    if(P.includ((point){u, v})) puts("Within");
	    else puts("Outside");
	}
    }
    return 0;
}