【网络流24题】餐巾计划（图解）

LOJ 6008【网络流24题】餐巾计划

题解

一张图片说明建图方法：

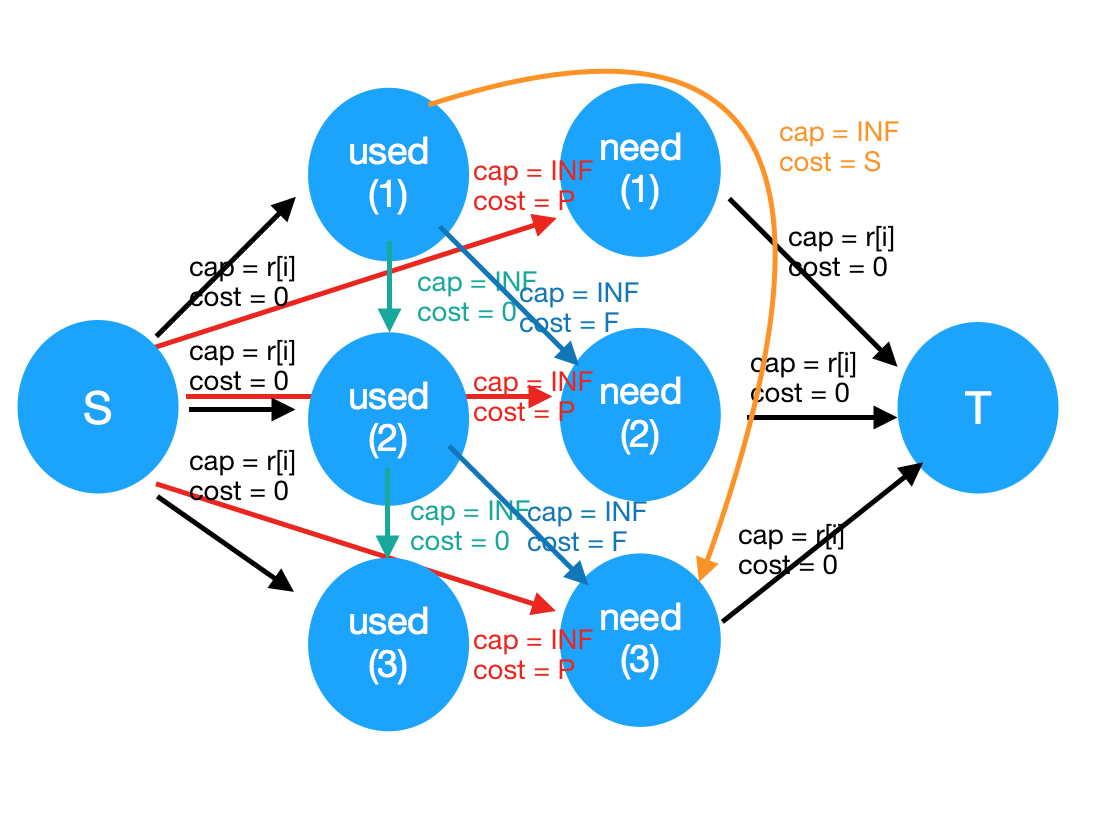
解说：

这种建图方法完美区分开了“脏餐巾”和“干净餐巾”两种餐巾。
每天一定会有r[i]个脏餐巾，所以源点向每天的“脏餐巾”（图上used）连边，容量r[i]，费用是0。另外，前一天的脏餐巾也可以留到下一天再处理，所以每天的used点向下一天的used点连一条边，容量INF，费用是0。
每天会需要r[i]个干净餐巾，所以每天的“干净餐巾”向汇点连边（图上need），干净餐巾可以由三种渠道获得：购买新餐巾（源点向它连边，容量INF，费用是P）、使用快洗（M天以前的used向它连边，容量INF，费用是F）、使用慢洗（N天以前的used向它连边，容量INF，费用是S）。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long ll;
#define space putchar(' ')
#define enter putchar('\n')
#define INF 0x3f3f3f3f
template <class T>
void read(T &x){
    char c;
    bool op = 0;
    while(c = getchar(), c < '0' || c > '9')
        if(c == '-') op = 1;
    x = c - '0';
    while(c = getchar(), c >= '0' && c <= '9')
        x = x * 10 + c - '0';
    if(op) x = -x;
}
template <class T>
void write(T x){
    if(x < 0) putchar('-'), x = -x;
    if(x >= 10) write(x / 10);
    putchar('0' + x % 10);
}

const int N = 2005, M = 200005;
int n, m, src, des, ans, dis[N];
int ecnt = 1, adj[N], cur[N], nxt[M], go[M], cap[M], cost[M];
bool inq[N], vis[N];
queue <int> que;

void ADD(int u, int v, int _cap, int _cost){
    go[++ecnt] = v;
    nxt[ecnt] = adj[u];
    adj[u] = ecnt;
    cap[ecnt] = _cap;
    cost[ecnt] = _cost;
}
void add(int u, int v, int _cap, int _cost){
    ADD(u, v, _cap, _cost);
    ADD(v, u, 0, -_cost);
}
bool bfs(){
    for(int i = 1; i <= des; i++)
        cur[i] = adj[i], dis[i] = INF, vis[i] = 0;
    dis[src] = 0, inq[src] = 1, que.push(src);
    while(!que.empty()){
        int u = que.front();
        inq[u] = 0, que.pop();
        for(int e = adj[u], v; e; e = nxt[e])
            if(cap[e] && dis[u] + cost[e] < dis[v = go[e]]){
                dis[v] = dis[u] + cost[e];
                if(!inq[v]) inq[v] = 1, que.push(v);
            }
    }
    return dis[des] < INF;
}
int dfs(int u, int flow){
    if(u == des) return ans += flow * dis[u], flow;
    vis[u] = 1;
    int ret = 0, delta;
    for(int &e = cur[u], v; e; e = nxt[e])
        if(cap[e] && !vis[v = go[e]] && dis[u] + cost[e] == dis[v]){
            delta = dfs(v, min(flow - ret, cap[e]));
            if(delta){
                cap[e] -= delta;
                cap[e ^ 1] += delta;
                ret += delta;
                if(ret == flow) break;
            }
        }
    return ret;
}

int P, F, S, Ftime, Stime;

int main(){

    read(n), read(P), read(Ftime), read(F), read(Stime), read(S);
    src = 2 * n + 1, des = 2 * n + 2;
    for(int i = 1, val; i <= n; i++){
        read(val);
        add(src, i, val, 0);
        add(i + n, des, val, 0);
        if(i > 1) add(i - 1, i, INF, 0);
        add(src, i + n, INF, P);
    }
    for(int i = 1; i + Ftime <= n; i++)
        add(i, i + Ftime + n, INF, F);
    for(int i = 1; i + Stime <= n; i++)
        add(i, i + Stime + n, INF, S);
    while(bfs()) dfs(src, INF);
    write(ans), enter;

    return 0;
}