小学生都能看懂的FFT!!!
小学生都能看懂的FFT!!!
前言
在创新实践中心偷偷看了一天FFT资料后,我终于看懂了一点。为了给大家提供一份简单易懂的学习资料,同时也方便自己以后复习,我决定动手写这份学习笔记。
食用指南:
本篇受众:如标题所示,另外也面向同我一样高中起步且非常菜的OIer。真正的dalao请无视。
本篇目标:让大家(和不知道什么时候把FFT忘了的我)在没有数学基础的情况下,以最快的速度了解并 会写 FFT。因此本篇将采用尽可能通俗易懂的语言,且略过大部分数学证明,在严谨性上可能有欠缺。但如果您发现了较大的逻辑漏洞,欢迎在评论里指正!最后……来个版权声明吧。本文作者胡小兔,博客地址http://rabbithu.cnblogs.com。暂未许可在任何其他平台转载。
你一定听说过FFT,它的高逼格名字让人望而却步——“快速傅里叶变换”。
你可能知道它可以\(O(n \log n)\)求高精度乘法,你想学,可是面对一堆公式,你无从下手。
那么欢迎阅读这篇教程!
[Warning] 本文涉及复数(虚数)的一小部分内容,这可能是最难的部分,但只要看下去也不是非常难,请不要看到它就中途退出啊QAQ。
什么是FFT?
快速傅里叶变换(FFT)是一种能在\(O(n \log n)\)的时间内将一个多项式转换成它的点值表示的算法。
补充资料:什么是点值表示
设\(A(x)\)是一个\(n - 1\)次多项式,那么把\(n\)个不同的\(x\)代入,会得到\(n\)个\(y\)。这\(n\)对\((x, y)\)唯一确定了该多项式,即只有一个多项式能同时满足“代入这些\(x\),得到的分别是这些\(y\)”。
由多项式可以求出其点值表示,而由点值表示也可以求出多项式。(并不想证明,十分想看证明的同学请前往“参考资料”部分)。
注:下文如果不加特殊说明,默认所有\(n\)为2的整数次幂。如果一个多项式次数不是2的整数次幂,可以在后面补0。
为什么要使用FFT?
FFT可以用来加速多项式乘法(平时非常常用的高精度大整数乘法就是最终把\(x = 10\)代入的多项式乘法)。
假设有两个\(n-1\)次多项式\(A(x)\)和\(B(x)\),我们的目标是——把它们乘起来。
普通的多项式乘法是\(O(n^2)\)的——我们要枚举\(A(x)\)中的每一项,分别与\(B(x)\)中的每一项相乘,来得到一个新的多项式\(C(x)\)。
但有趣的是,两个用点值表示的多项式相乘,复杂度是\(O(n)\)的!具体方法:\(C(x_i) = A(x_i) \times B(x_i)\),所以\(O(n)\)枚举\(x_i\)即可。
要是我们把两个多项式转换成点值表示,再相乘,再把新的点值表示转换成多项式岂不就可以\(O(n)\)解决多项式乘法了!
……很遗憾,显然,把多项式转换成点值表示的朴素算法是\(O(n^2)\)的。另外,即使你可能不会——把点值表示转换为多项式的朴素“插值算法”也是\(O(n^2)\)的。
难道大整数乘法就只能是\(O(n^2)\)吗?!不甘心的同学可以发现,大整数乘法复杂度的瓶颈可能在“多项式转换成点值表示”这一步(以及其反向操作),只要完成这一步就可以\(O(n)\)求答案了。如果能优化这一步,岂不美哉?
傅里叶:这个我会!
离散傅里叶变换(快速傅里叶变换的朴素版)
傅里叶发明了一种办法:规定点值表示中的\(n\)个\(x\)为\(n\)个模长为\(1\)的复数。
——等等,先别看到复数就走!
补充资料:什么是复数
如果你学过复数,这段不用看了;
如果你学过向量,请把复数理解成一个向量;
如果你啥都没学过,请把复数理解成一个平面直角坐标系上的点。复数具有一个实部和一个虚部,正如一个向量(或点)有一个横坐标和一个纵坐标。例如复数\(3 + 2i\),实部是\(3\),虚部是\(2\),\(i = \sqrt{-1}\)。可以把它想象成向量\((3, 2)\)或点\((3, 2)\)。
但复数比一个向量或点更妙的地方在于——复数也是一种数,它可以像我们熟悉的实数那样进行加减乘除等运算,还可以代入多项式\(A(x)\)——显然你不能把一个向量或点作为\(x\)代入进去。
复数相乘的规则:模长相乘,幅角相加。模长就是这个向量的模长(或是这个点到原点的距离);幅角就是x轴正方向逆时针旋转到与这个向量共线所途径的角(或是原点出发、指向x轴正方向的射线逆时针旋转至过这个点所经过的角)。想学会FFT,“模长相乘”暂时不需要了解过多,但“幅角相加”需要记住。
C++的STL提供了复数模板!
头文件:#include <complex>
定义: complex<double> x;
运算:直接使用加减乘除。
傅里叶要用到的\(n\)个复数,不是随机找的,而是——把单位圆(圆心为原点、1为半径的圆)\(n\)等分,取这\(n\)个点(或点表示的向量)所表示的虚数,即分别以这\(n\)个点的横坐标为实部、纵坐标为虚部,所构成的虚数。
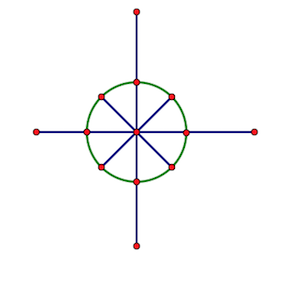
从点\((1, 0)\)开始(显然这个点是我们要取的点之一),逆时针将这\(n\)个点从\(0\)开始编号,第\(k\)个点对应的虚数记作\(\omega_n^k\)(根据复数相乘时模长相乘幅角相加可以看出,\(\omega_n^k\)是\(\omega_n^1\)的\(k\)次方,所以\(\omega_n^1\)被称为\(n\)次单位根)。
根据每个复数的幅角,可以计算出所对应的点/向量。\(\omega_n^k\)对应的点/向量是\((\cos \frac{k}{n}2\pi, \sin \frac{k}{n}2\pi)\),也就是说这个复数是\(\cos \frac{k}{n}2\pi + i\sin \frac{k}{n}2\pi\)。
傅里叶说:把\(n\)个复数\(\omega_n^0, \omega_n^1, \omega_n^2, ..., \omega_n^{n-1}\)代入多项式,能得到一种特殊的点值表示,这种点值表示就叫离散傅里叶变换吧!
[Warning] 从现在开始,本文个别部分会集中出现数学公式,但是都不是很难,公式恐惧症患者请坚持!Stay Determined!
补充资料:单位根的性质
性质一:\(\omega_{2n}^{2k} = \omega_{n}^{k}\)
证明:它们对应的点/向量是相同的。
性质二:\(\omega_{n}^{k + \frac{n}{2}} = -\omega_{n}^{k}\)
证明:它们对应的点是关于原点对称的(对应的向量是等大反向的)。
为什么要使用单位根作为\(x\)代入
当然是因为离散傅里叶变换有着特殊的性质啦。
[Warning] 下面有一些证明,如果不想看,请跳到加粗的“一个结论”部分。
设\((y_0, y_1, y_2, ..., y_{n - 1})\)为多项式\(A(x) = a_0 + a_1x + a_2x^2 +...+a_{n-1}x^{n-1}\)的离散傅里叶变换。
现在我们再设一个多项式\(B(x) = y_0 + y_1x + y_2x^2 +...+y_{n-1}x^{n-1}\),现在我们把上面的\(n\)个单位根的倒数,即\(\omega_{n}^{0}, \omega_{n}^{-1}, \omega_{n}^{-2}, ..., \omega_{n}^{-(n - 1)}\)作为\(x\)代入\(B(x)\), 得到一个新的离散傅里叶变换\((z_0, z_1, z_2, ..., z_{n - 1}\))。
这个\(\sum_{i = 0}^{n - 1}(\omega_n^{j - k})^i\)是可求的:当\(j - k = 0\)时,它等于\(n\); 其余时候,通过等比数列求和可知它等于\(\frac{(\omega_n^{j - k})^n - 1}{\omega_n^{j - k} - 1} = \frac{(\omega_n^n)^{j - k} - 1}{\omega_n^{j - k} - 1} = \frac{1^{j - k}- 1}{\omega_n^{j - k} - 1} = 0\)。
那么,\(z_k\)就等于\(na_k\), 即:
一个结论
把多项式\(A(x)\)的离散傅里叶变换结果作为另一个多项式\(B(x)\)的系数,取单位根的倒数即\(\omega_{n}^{0}, \omega_{n}^{-1}, \omega_{n}^{-2}, ..., \omega_{n}^{-(n - 1)}\)作为\(x\)代入\(B(x)\),得到的每个数再除以n,得到的是\(A(x)\)的各项系数。这实现了傅里叶变换的逆变换——把点值表示转换成多项式系数表示,这就是离散傅里叶变换神奇的特殊性质。
快速傅里叶变换
虽然傅里叶发明了神奇的变换,能把多项式转换成点值表示又转换回来,但是……它仍然是暴力代入的做法,复杂度仍然是\(O(n^2)\)啊!(傅里叶:我都没见过计算机,我干啥要优化复杂度……)
于是,快速傅里叶变换应运而生。它是一种分治的傅里叶变换。
[Warning] 下面有较多公式。看起来很吓人,但是并不复杂。请坚持看完。
快速傅里叶变换的数学证明
仍然,我们设\(A(x) = a_0 + a_1x + a_2x^2 +...+a_{n-1}x^{n-1}\),现在为了求离散傅里叶变换,要把一个\(x = \omega_n^k\)代入。
考虑将\(A(x)\)的每一项按照下标的奇偶分成两部分:
设两个多项式:
则:
假设\(k < \frac{n}{2}\),现在要把\(x = \omega_n^k\)代入:
那么对于\(A(\omega_n^{k + \frac{n}{2}})\):
所以,如果我们知道两个多项式\(A_1(x)\)和\(A_2(x)\)分别在\((\omega_{\frac{n}{2}}^{0}, \omega_{\frac{n}{2}}^{1}, \omega_{\frac{n}{2}}^{2}, ... , \omega_{\frac{n}{2}}^{\frac{n}{2} - 1}\))的点值表示,就可以\(O(n)\)求出\(A(x)\)在\(\omega_n^0, \omega_n^1, \omega_n^2, ..., \omega_n^{n-1}\)处的点值表示了。而\(A_1(x)\)和\(A_2(x)\)都是规模缩小了一半的子问题。分治边界是\(n = 1\),此时直接return。
快速傅里叶变换的实现
写个递归就可以实现一个FFT了!
cp omega(int n, int k){
return cp(cos(2 * PI * k / n), sin(2 * PI * k / n));
}
void fft(cp *a, int n, bool inv){
if(n == 1) return;
static cp buf[N];
int m = n / 2;
for(int i = 0; i < m; i++){ //将每一项按照奇偶分为两组
buf[i] = a[2 * i];
buf[i + m] = a[2 * i + 1];
}
for(int i = 0; i < n; i++)
a[i] = buf[i];
fft(a, m, inv); //递归处理两个子问题
fft(a + m, m, inv);
for(int i = 0; i < m; i++){ //枚举x,计算A(x)
cp x = omega(n, i);
if(inv) x = conj(x);
//conj是一个自带的求共轭复数的函数,精度较高。当复数模为1时,共轭复数等于倒数
buf[i] = a[i] + x * a[i + m]; //根据之前推出的结论计算
buf[i + m] = a[i] - x * a[i + m];
}
for(int i = 0; i < n; i++)
a[i] = buf[i];
}
inv表示这次用的单位根是否要取倒数。
至此你已经会写fft了!但是这个fft还是1.0版本,比较慢(可能同时还比较长?),亲测可能会比加了一些优化的fft慢了4倍左右……
那么我们来学习一些优化吧!
优化fft
非递归fft
在进行fft时,我们要把各个系数不断分组并放到两侧,那么一个系数原来的位置和最终的位置有什么规律呢?
初始位置:0 1 2 3 4 5 6 7
第一轮后:0 2 4 6|1 3 5 7
第二轮后:0 4|2 6|1 5|3 7
第三轮后:0|4|2|6|1|5|3|7
“|”代表分组界限。
可以发现(这你都能发现?),一个位置a上的数,最后所在的位置是“a二进制翻转得到的数”,例如6(011)最后到了3(110),1(001)最后到了4(100)。
那么我们可以据此写出非递归版本fft:先把每个数放到最后的位置上,然后不断向上还原,同时求出点值表示。
代码:
cp a[N], b[N], omg[N], inv[N];
void init(){
for(int i = 0; i < n; i++){
omg[i] = cp(cos(2 * PI * i / n), sin(2 * PI * i / n));
inv[i] = conj(omg[i]);
}
}
void fft(cp *a, cp *omg){
int lim = 0;
while((1 << lim) < n) lim++;
for(int i = 0; i < n; i++){
int t = 0;
for(int j = 0; j < lim; j++)
if((i >> j) & 1) t |= (1 << (lim - j - 1));
if(i < t) swap(a[i], a[t]); // i < t 的限制使得每对点只被交换一次(否则交换两次相当于没交换)
}
static cp buf[N];
for(int l = 2; l <= n; l *= 2){
int m = l / 2;
for(int j = 0; j < n; j += l)
for(int i = 0; i < m; i++){
buf[j + i] = a[j + i] + omg[n / l * i] * a[j + i + m];
buf[j + i + m] = a[j + i] - omg[n / l * i] * a[j + i + m];
}
for(int j = 0; j < n; j++)
a[j] = buf[j];
}
}
可以预处理\(\omega_n^k\)和\(\omega_n^{-k}\),分别存在omg和inv数组中。调用fft时,如果无需取倒数,则传入omg;如果需要取倒数,则传入inv。
蝴蝶操作
这个优化有着一个高大上的名字——“蝴蝶操作”。我第一次看到这个名字时就吓跑了——尤其是看到那种带示意图的蝴蝶操作解说时。
但是你完全无需跑!这是一个很简单的优化,它可以丢掉上面代码里的那个buf数组。
我们为什么需要buf数组?因为我们要做这两件事:
a[j + i] = a[j + i] + omg[n / l * i] * a[j + i + m]
a[j + i + m] = a[j + i] - omg[n / l * i] * a[j + i + m]
但是我们又要求这两行不能互相影响,所以我们需要buf数组。
但是如果我们这样写:
cp t = omg[n / l * i] * a[j + i + m]
a[j + i + m] = a[j + i] - t
a[j + i] = a[j + i] + t
就可以原地进行了,不需要buf数组。
cp a[N], b[N], omg[N], inv[N];
void init(){
for(int i = 0; i < n; i++){
omg[i] = cp(cos(2 * PI * i / n), sin(2 * PI * i / n));
inv[i] = conj(omg[i]);
}
}
void fft(cp *a, cp *omg){
int lim = 0;
while((1 << lim) < n) lim++;
for(int i = 0; i < n; i++){
int t = 0;
for(int j = 0; j < lim; j++)
if((i >> j) & 1) t |= (1 << (lim - j - 1));
if(i < t) swap(a[i], a[t]); // i < t 的限制使得每对点只被交换一次(否则交换两次相当于没交换)
}
for(int l = 2; l <= n; l *= 2){
int m = l / 2;
for(cp *p = a; p != a + n; p += l)
for(int i = 0; i < m; i++){
cp t = omg[n / l * i] * p[i + m];
p[i + m] = p[i] - t;
p[i] += t;
}
}
}
现在,这个fft就比之前的递归版快很多了!
到此为止我的FFT笔记就整理完啦。
下面贴一个FFT加速高精度乘法的代码:
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <complex>
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
typedef long long ll;
template <class T>
void read(T &x){
char c;
bool op = 0;
while(c = getchar(), c < '0' || c > '9')
if(c == '-') op = 1;
x = c - '0';
while(c = getchar(), c >= '0' && c <= '9')
x = x * 10 + c - '0';
if(op) x = -x;
}
template <class T>
void write(T x){
if(x < 0) putchar('-'), x = -x;
if(x >= 10) write(x / 10);
putchar('0' + x % 10);
}
const int N = 1000005;
const double PI = acos(-1);
typedef complex <double> cp;
char sa[N], sb[N];
int n = 1, lena, lenb, res[N];
cp a[N], b[N], omg[N], inv[N];
void init(){
for(int i = 0; i < n; i++){
omg[i] = cp(cos(2 * PI * i / n), sin(2 * PI * i / n));
inv[i] = conj(omg[i]);
}
}
void fft(cp *a, cp *omg){
int lim = 0;
while((1 << lim) < n) lim++;
for(int i = 0; i < n; i++){
int t = 0;
for(int j = 0; j < lim; j++)
if((i >> j) & 1) t |= (1 << (lim - j - 1));
if(i < t) swap(a[i], a[t]); // i < t 的限制使得每对点只被交换一次(否则交换两次相当于没交换)
}
for(int l = 2; l <= n; l *= 2){
int m = l / 2;
for(cp *p = a; p != a + n; p += l)
for(int i = 0; i < m; i++){
cp t = omg[n / l * i] * p[i + m];
p[i + m] = p[i] - t;
p[i] += t;
}
}
}
int main(){
scanf("%s%s", sa, sb);
lena = strlen(sa), lenb = strlen(sb);
while(n < lena + lenb) n *= 2;
for(int i = 0; i < lena; i++)
a[i].real(sa[lena - 1 - i] - '0');
for(int i = 0; i < lenb; i++)
b[i].real(sb[lenb - 1 - i] - '0');
init();
fft(a, omg);
fft(b, omg);
for(int i = 0; i < n; i++)
a[i] *= b[i];
fft(a, inv);
for(int i = 0; i < n; i++){
res[i] += floor(a[i].real() / n + 0.5);
res[i + 1] += res[i] / 10;
res[i] %= 10;
}
for(int i = res[lena + lenb - 1] ? lena + lenb - 1: lena + lenb - 2; i >= 0; i--)
putchar('0' + res[i]);
enter;
return 0;
}
博客地址:http://rabbithu.cnblogs.com


