【Mathematical Model】基于Python的相关性/显著性分析&成图

        很久之前编写的代码了，当时是用来分析遥感波段组合对于某地物反演的相关性分析。今天正好整理数据时一块分享出来。

原创作者：RS迷途小书童

博客地址：https://blog.csdn.net/m0_56729804?type=blog

1 相关性的概念

        “相关性”是统计学中的一个基本概念，它用来描述两个或多个变量之间关系的强度和方向。简单来说，如果两个变量之间存在一种可以观测到的、一致性的变化趋势，那么我们就可以说这两个变量是相关的。

2 相关性的类型

1. 正相关：当一个变量增加时，另一个变量也倾向于增加，或者当一个变量减少时，另一个变量也倾向于减少。这种关系被称为正相关。

2. 负相关：当一个变量增加时，另一个变量倾向于减少，反之亦然。这种关系被称为负相关。

3. 零相关：两个变量之间没有明显的变化趋势或关系，即一个变量的变化对另一个变量没有显著影响。

3 相关性的衡量方法

1. 相关系数：最常用的衡量两个变量之间线性相关程度的方法是计算相关系数，如皮尔逊相关系数（Pearson correlation coefficient）和斯皮尔曼等级相关系数（Spearman's rank correlation coefficient）。皮尔逊相关系数适用于度量两个连续变量之间的线性关系强度和方向，其值介于-1和1之间。值为1表示完全正相关，值为-1表示完全负相关，值为0表示无线性相关。

2. 散点图：通过绘制两个变量的散点图，可以直观地观察它们之间的关系。如果点呈现出明显的线性排列趋势，则两个变量可能具有相关性。

4 Python代码

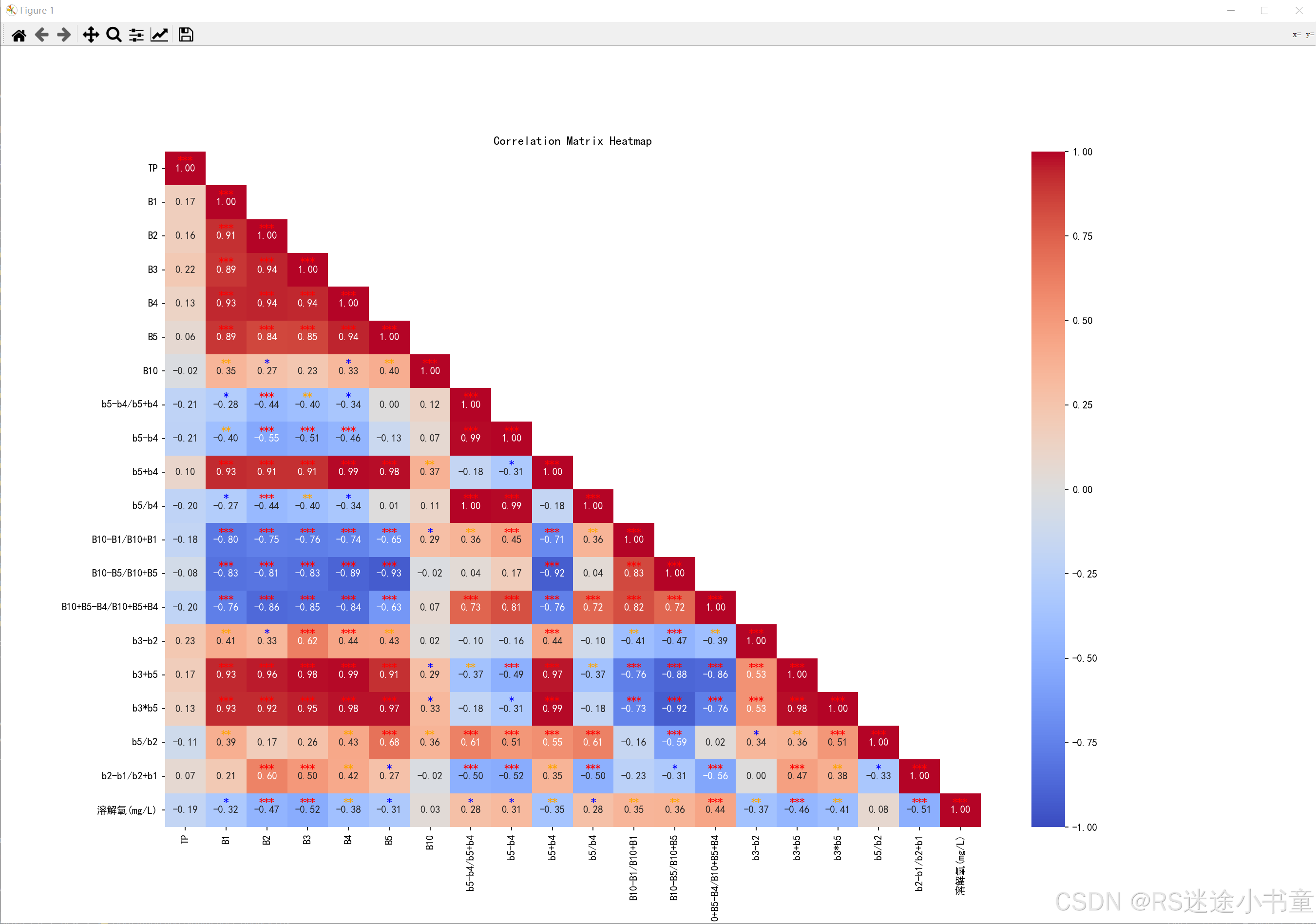
        代码中直接通过读取excel表格作相关性分析，具体数据格式为第一行为列名，下面为数据，结果即为每一列之间的相关性。

# -*- coding: utf-8 -*-
"""
@Time ： 2024/3/8 11:31
@Auth ： RS迷途小书童
@File ：Correlation and Significance Analysis.py
@IDE ：PyCharm
@Purpose：相关性/显著性分析+出图(表格第一行为列名)
@Web：博客地址:https://blog.csdn.net/m0_56729804
"""
import numpy as np
import pandas as pd
import seaborn as sns
import scipy.stats as stats
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


def analysis(path_excel):
    """
    :param path_excel: 输入数据表格，格式为：第一行列名（包含x,y）
    :return: None
    data = np.array([[1, 1, 3, 6, 2],
                     [26, 33, 28, 31, 27],
                     [13, 20, 15, 18, 14]])
    print(np.corr coe f(data))
    print(np.corr coe f(data, row var=0))  # 用于计算列之间的相关系数
    """
    df = pd.read_excel(path_excel)
    correlation = df.corr()  # 计算相关性
    # df_coo = df.corr(method=lambda x, y: pearsonr(x, y)[0])
    print(correlation)
    fig, ax = plt.subplots(figsize=(18, 12), facecolor='w')  # 指定颜色带的色系
    mask = np.tril(np.ones(correlation.values.shape, dtype=int))
    mask = np.where(mask == 1, 0, 1)
    # 制作掩膜，去除右上角部分
    sns.heatmap(correlation, annot=True, cmap="coolwarm", mask=mask, vmax=1, vmin=-1, fmt='.2f', ax=ax)
    # annot_kws={"color": "k"}字体颜色。cmap="Blues","RdBu_r"图例颜色
    plt.title('Correlation Matrix Heatmap')
    # for m in ax.get_xticks():
    #     for n in ax.get_yticks():
    #         x = df.iloc[:, int(m)]
    #         y = df.iloc[:, int(n)]
    #         corr_c, p_value = stats.pearsonr(x, y)  # 计算相关性/显著性
    #         # print(int(m), int(n), correlation.values[int(m), int(n)], corr_c, p_value)
    #         if mask[int(m), int(n)] < 1.:
    #             if p_value < 0.001:
    #                 ax.text(n, m - 0.15, '***', ha='center', color='red')
    #             elif p_value < 0.01:
    #                 ax.text(n, m - 0.15, '**', ha='center', color='orange')
    #             elif p_value < 0.05:
    #                 ax.text(n, m - 0.15, '*', ha='center', color='blue')
    plt.show()
    # plt.savefig('Correlation Matrix Heatmap', dpi=500)


if __name__ == "__main__":
    path = r'Z:\彭俊喜/2.xlsx'
    analysis(path)

        代码中注释掉的是显著性分析的可视化效果，可以不要。

5 效果图

​

​