求最长回文字串(Palindrome)
参考:
1. 最长回文子串
2. Manacher 算法
回文字符串指的是一个字符串从左到右读和从右到左读是完全一样的,比如"abba"或"abcba“。
字符串中最长的回文串,就是找到一个字符串里面,最长的连续字符可以组成一个回文字符串的子串,比如"abvvcvba"中的"vcv"。
解决方法:
1. 暴力解决 - 复杂度$\Theta(n^2)$
2. 动态规划 - 复杂度$\Theta(n^2)$
3. 中心扩展 - 复杂度$\Theta(n^2)$
4. 马拉车算法(Manacher) - 复杂度$\Theta(n)$
1. 暴力解决:
遍历每一个字串,并判断是否回文串,当长度比原记录的最大长度长时,更新最大长度。
python:
#Palindrome-way-1 #0. record the maximum of Palindrome substring with Mlen = 0; and its start with startInd. #1. see into every substring #2. check if it is a Palindrome #3. compare the length with Mlen and update Mlen & startInd if needed def checkPal(string): #if the string is a palindrome, then return the length, otherwise return 0 if string[::-1] == string: return len(string) else: return 0 def findMaxPal(string): Mlen = 0 for i in range(0, len(string)): for j in range(i+1, len(string)+1): currlen = checkPal(testStr[i:j]) if currlen > Mlen: Mlen = currlen startInd = i return startInd, Mlen testStr = "helloifyoucanac" result = findMaxPal(testStr) testStr[result[0]:(result[0]+result[1])]
C++:
2. 动态规划:
从长度入手,遍历每一个可能的长度,找到符合长度的字符串,用矩阵M记录。比如M[1, 3] = 1表示string[1:4]是个回文字符串,为0则表示不是。由于一个回文串长度是N的基础,在于它的一个N-2长度的字串也是回文串,更严格的,当string[i:j]为回文串时,string[i+1,j-1]也是回文串。所以从最小的长度开始遍历起,往后判断更大的长度的字符串是否为回文串时,只需要判断它的小子串是不是回文串,以及(相对于小子串而言)新扩展的左右两个字符是否相同。
这里把长度为2的部分单独拿出来,是因为判断和长度大于3的部分有些不同。加上flag只是为了不用出现相同长度的回文串时多次给Mlen和startInd赋值,减少的计算量似乎也不多。
python:
#Palindrome-way-2 dynamic programming #0. record the maximum of Palindrome substring with Mlen = 0; and its start with startInd. #1. initial a matrix M with all dignonal elements = 1 and others =0 # M(i, j) records if string[i, j+1] is a palindrome or not # if string[i, j+1] is a palindrome, then we just need to check if string[i-1] = string[j+1] or not #2. for length of the substring to loop, check if the substrings of that length is palindrome. # the point is for a fixed length, the check operation is the same: check a pair of char #3. update the matrix M import numpy as np def findMaxPal_2(string): M = np.zeros((len(string), len(string)), dtype = int) Mlen = 1 flag = 0 # if Mlen is larger than Mlen of the former round for i in range(len(string)): M[i][i] = 1 for i in range(len(string)-1): #for the situation of length = 2, which is not easily corporated into the below code if string[i] == string[i+1]: M[i][i+1] = 1 if flag == 0: flag = 1 Mlen = 2 startInd = i flag = 0 for slen in range(3, len(string)): for i in range(len(string)-slen): # i is the index of start of the substring j = i + slen -1 if (M[i+1][j-1] == 1) & (string[i] == string[j]): M[i][j] = 1 if flag == 0: flag = 1 Mlen = slen startInd = i flag = 0 return startInd, Mlen testStr = "helloifyoucanac" #testStr = "if youcannacuoif" result = findMaxPal_2(testStr) testStr[result[0]:(result[0]+result[1])]
C++:
3. 中心拓展:
每一个回文串如果是奇数长度,则会有一个字符为中心,如"aba"中心是"b";如果是偶数长度,如"abba",那么视"bb"为中心,中心起始点为第一个"b"。
这个算法的想法是从字符开始遍历,去判断以这个字符为中心的回文串是否存在以及最大长度多少。
记当前中心为curr,对于奇数情况,slen从小到大,顺序判断string[curr+slen] = string[curr-slen]是否成立,即知道string[(curr-slen):(curr+slen+1)]是否为回文串
对于偶数情况,先判断该字符右边第一个字符是否与之相同(或者左边第一个也可以,相应地需要对代码进行调整),然后slen从小到大变化,顺序判断string[curr+slen+1] = string[curr-slen]是否成立,即知道string[(curr-slen):(curr+slen+1)]是否为回文串。
python:
#Palindrome-way-3 expand by center #0. record the maximum of Palindrome substring with Mlen = 1; and its start with startInd; L the length of the string #1. for every char with index curr # for odd situation, while (curr+slen) < L & (curr-slen) >= 0, check if string[curr-slen] = string[curr+slen] # for ever situation , while (curr+slen+1) < L & (curr-slen) > 0, check if string[curr] = string[curr+1] & string[curr-slen] = string[curr+slen+1] #2. compare the 2*slen-1 or 2*slen with Mlen and update Mlen & startInd if needed def findMaxPal_3(string): Mlen = 1 startInd = 0 L = len(string) slen = 1 # if string = "cabac", curr = 2, then slen = 3. if "acca", curr = 1 then slen = 2 # odd situation for curr in range(1, L-1, 1): while ((curr+slen) < L) & ((curr-slen) >= 0): if string[curr+slen] == string[curr-slen]: slen += 1 else: break if (2*slen - 1) > Mlen: # 2*(slen-1)+1 > Mlen Mlen = 2*slen - 1 startInd = curr-slen+1 # curr-(slen-1) slen = 1 # even situation for curr in range(L-1): if string[curr] == string[curr+1]: while ((curr+slen+1) < L) & ((curr-slen) > 0): if string[curr+slen+1] == string[curr-slen]: slen += 1 else: break if (2*slen) > Mlen: Mlen = 2*slen startInd = curr-slen+1 # curr-(slen-1) slen = 1 return startInd, Mlen testStr = "abaccabcb" result = findMaxPal_3(testStr) testStr[result[0]:(result[0]+result[1])]
C++:
4. 马拉车算法
这个算法主要用了两个技巧:
1. 给原字符串的每个字符间隔都加上"#“,并在首位补"$\$$”,末尾补"\0“(C++字符串判定字符串介绍的标记。如果是python,可以挑一个和"#”"$\$$“都不一样的字符,如"&”)。加入字符串的这些字符都必须在原字符串中没有出现。通过这样的方式,长度为$L$的字符串长度变为$2*L+3$,不管原来是奇数还是偶数长度,现在都是奇数长度。在判断回文的时候就可以不区分奇偶了。处理过后的字符串最长的回文长度半径,就是原字符串最长的回文长度。如"cabad“处理之后为"$\$$#c#a#b#a#d#&",这个新字符串以"b"为中心,半径为3(左边"#a#",右边"#a#")。
2. 新建一个数组(或列表等)存储每一个字符对应的以其为中心时最大的回文半径(这里的半径定义也可以是再加上自身,即再加1,但原理不变):
| ind | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| s_new[i] | $ | # | c | # | a | # | b | # | a | # | d | # | e | # | e | # | d | # | a | # | & |
| rad[i] | 0 | 0 | 1 | 0 | 1 | 0 | 3 | 0 | 1 | 0 | 1 | 1 | 1 | 6 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
而后考虑到,当某个$ind$(如5)已经被判断过时,其前面的字符都已经过判断(对应5的0、1、2、3、4),则它们的半径$rad$也已经过计算。
记当前计算得到的回文串中最右的边界为$edgeR$(不一定是最长的回文串的右边界,这里是为了尽可能地覆盖还未进行判断的字符,以节省计算),其对应的回文串的中心为$id$,从上一句话可以判断出来,$id$一定在当前等待计算的字符位置$curr$的左边,而$rad(curr)$可以通过前面的信息判断出来,具体见下面分析。
记$edgeR$关于$id$的对称点为$edgeL$,$curr$关于$id$的对称点为$curr_s$,则它们的位置关系如下所示:
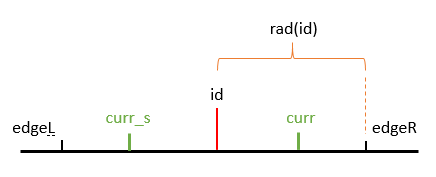
则$rad(curr)$的长度为$min(edgeR-curr, rad(curr_s))$,此后只需要判断超出$edgeR$的部分是否还存在对称字符,$rad(curr)$再增加。
这是因为,
当$edgeR-curr > rad(curr_s)$时,则$rad(curr) = rad(curr_s)$,因为它们被覆盖在$[edgeL, edgeR]$这个区间里的部分是相互对应的,如若不等会导致矛盾。此时判断在$curr+rad(curr_s)$外的字符是否与$curr-rad(curr_s)$相等会是FALSE。
当$rad(curr_s) > edgeR-curr$时,则$rad(curr) < rad(curr_s)$并且$rad(curr)=edgeR-curr$。以$curr$为中心的回文串要延长,只能是超过$edgeR$的部分,如果此时有$rad(curr) > edgeR-curr$,那么超出$edgeR$和$edgeL$的部分也会出现对称的字符,此时$rad(id) > edgeR-id$,产生矛盾。此时判断在$curr+(edgeR-curr)$外的字符是否与$curr-(edgeR-curr)$对应的字符相等,也即$curr+rad(id)$和$curr-rad(id)$对应的字符不相等。
当$rad(curr_s) = edgeR-curr$时,以$curr$为中心的回文串要延长,只能是超过$edgeR$的部分,所以这个时候只要再往外判断就可以了,不需要再判断$curr$右侧、$edgeR$左侧这些字符与$curr$左侧的对称性。
python:
#Palindrome-way-4 Manacher #0. add the "#"s to the string. # record the maximum of Palindrome substring with Mlen = 1; and its start with startInd = 2; L the length of the string # record the current rightest edge of palindrome with edgeR, initialize it with 2, and the index of the character is named id = 2 # record the current index with curr, and its symmetric index about id is curr_s = 2*curr - id # record the length of the palidromes centred by the characters with list rad #1. for every char with index curr # slen = 0 # check if edgeR > curr, if true, then make rad[curr] = min(rad(curr_s), edgeR-curr) and slen = rad[curr]+1 # while(string[curr-slen] = string[curr+slen]) slen++ & rad[curr]++ # if curr+rad[curr] > edgeR, then edgeR = curr+slen, id = curr #2. Mlen = max(rad) # startInd = floor((argmax(rad)-2)/2) : the real index of the original string import numpy as np def initStr(string): s_new = ["#"]*(2*len(string)+3) s_new[0] = "$" s_new[-1] = "&" for i in range(len(string)): s_new[2*i+2] = string[i] return s_new def findMaxPal_4(string): s_new = initStr(string) Mlen = 1 startInd = 2 L = len(s_new) edgeR = 2 id_ = 2 curr = 2 #curr_s = 2*id_- curr rad = [0]*L for curr in range(2, L-1, 1): slen = 1 if curr < edgeR: rad[curr] = min(edgeR - curr, rad[2*id_-curr]) # curr_s = 2*id_-curr slen = rad[curr]+1 while s_new[curr+slen] == s_new[curr-slen]: slen += 1 rad[curr] = slen-1 if (curr + rad[curr]) > edgeR: id_ = curr edgeR = curr + rad[curr] Mlen = max(rad) startInd = int((np.argmax(rad)-Mlen-1)/2) # np.argmax(rad)-Mlen+1: original start index return startInd, Mlen testStr = "abbadafadb" result = findMaxPal_4(testStr) testStr[result[0]:(result[0]+result[1])]
C++:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号