数据
属性的类型
1、标称:标称属性的值仅仅只是不同的名字,即标称值只提供足够的信息以区分对象。邮编、雇员ID、颜色、性别。
2、序数:序数属性的值提供足够的信息确定对象的序 。矿石硬度(好,较好,最好)、成绩、街道号码
3、区间:对于符号属性,值之间的差是有意义的,即存在测量单位。日历日期、摄氏温度华氏温度。
4、比率:对于比率变量,差和比率都是有意义的。绝对温度, 货币量, 计数, 年龄, 质量, 长度, 电流
离散属性和连续属性:
离散属性
–具有有限个值或无限可数个值
–例如: 邮政编码, 计数, 或一个文档集合中词的集合
–常用整数变量表示.
–注: 二元属性是离散属性的一种特殊情况
连续属性
–取实数值的属性
–例如: 温度,高度或重量.
–实践中, 实数值只能用有限的精度测量和表示.
–通常,连续属性用浮点变量表示
数据集的类型:
1、记录数据
–数据矩阵
–文档数据
–事物数据
2、图形数据
–万维网
–分子结构
3、有序数据
–空间数据
–时间序列数据
–时序数据
–基因序列数据
离群点:
离群点是在某种意义上具有不同于数据集中其他大部分数据对象的特征的数据对象,或是相对于该属性的典型值来说不寻常的属性值
缺失值:
缺失值原因:没有被收集的数据信息(有的人拒绝透露年龄体重),属性不能用于所有对象(年收入不适用于儿童)
处理缺失值:
删除数据对象或属性,估计缺失值,在分析中忽略缺失值,用所有可能的值替换(权重是他们对应的概率)
重复值:数据集可能包含重复或几乎重复的数据对象
数据的预处理:聚集、抽样、维规约、特征子集选择、特征创建、离散化和二元化、变量变换
一、聚集:将两个或多个对象(或属性)合并成单个对象(或属性)。目的:1、数据规约,减少属性或对象的数量,2、范围或标度转换,城市被聚集成区域,洲或国家等等,3、更稳定的数据,聚集的数据秦翔宇具有较小的变异性。
二、抽样:数据挖掘使用抽样是因为处理所有的数据的费用太高或太浪费时间。
抽样方法:1、简单随机抽样,选取任何特定项的概率相等,2、无放回抽样,每个选中项立即从构成总体的所有对象集中删除,3、有放回抽样对象被选中时不从总体中删除。4、分层抽样,把数据几个组(部分),然后从每个组(部分)进行随机抽样
三、维灾难:随着维度的增加,数据在它所占据的空间中越来越稀疏,点之间的密度和距离的定义失去了意义,而密度和距离对于聚类和离群点检测是至关重要的
维规约的目的就是为了避免维灾难,降低数据挖掘算法的时间和内存的需求,让数据更容易可视化,可以删除不相关的特征并降低噪声。主要的方法有主成分分析,奇异值分解,其他有监督的和非线性的技术。
降低数据维度的另一种方法是选择特征子集
选择的方法:
1、蛮力方法:
将所有可能的特征子集作为感兴趣的数据挖掘算法的输入,然后选取产生最好结果的子集
2、嵌入方法:
特征选择作为数据挖掘算法的一部分是理算当然的
3、过滤方法:
使用某种独立于数据挖掘任务的方法,在数据挖掘算法运行前进行特征选择
4、包装方法:
将目标数据挖掘算法作为黑箱,使用类似于前面介绍的理想算法,但通常并不枚举所有可能的子集来找出最佳属性子集
特征创建的方法:常常可以由原来的属性创建新的属性集,更有效地捕获数据集中的重要信息
三个主要的方法:
1、特征提取
领域-特定的
2、映射数据到新的空间 傅里叶变换和小波变换
3、特征构造
整合(结合)特征,一个或多个由原特征构造的新特征
四、使用类别标签离散化:基于熵的方法
五、变量变换:一个函数把数据集中一个给定属性的值映射到一个替代值的新的数集,使得任何一个旧值能被其中一个新值确定。简单函数xk, log(x), ex, |x|,标准化和规范化
相似性和相异性:
1、相似度
–两个对象相似程度的数值度量.
–两个对象越相似,它们的相似度就越高.
–相似度非负,常在 [0,1]内取值
2、相异度
–两个对象差异程度的数值度量
–对象越相似,它们的相异度越低
–相异度的最小值常是0
–上限是无穷大
邻近度用来表示相似性或相异性
欧几里得距离:
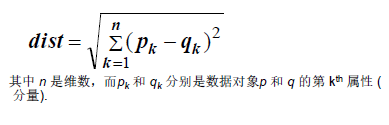
闵可夫斯基距离:
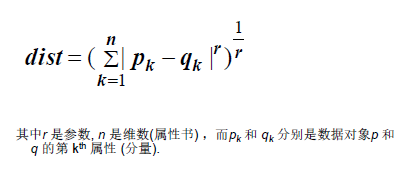
闵可夫斯基距离例子
1、r = 1. 街区距离(曼哈顿, 出租车, L1 范数) 距离。
曼哈顿距离:
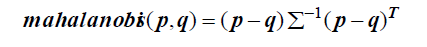
是输入数据X的协方差矩阵
一个常见的例子是汉明距离, 它是具有二元属性的对象(即两个二元向量)之间不同的二进制位个数
2、r = 2. 欧几里得距离
是对象属性之间的最大距离
注意不要将参数r 和维数(属性) n混淆, 欧几里得距离、曼哈顿距离和上确界距离是对n的所有值(1,2,3,…)定义的,并且指定了将每个维(属性)上的差的组合成总距离的不同方法。
距离的共有性质:
1.非负性 a. 对所有的p 和 q ,d(p, q) 0,b.仅当 p = q 时,有 d(p, q) = 0
2.对称性 对于所有p 和 q,有 d(p, q) = d(q, p)
3.三角不等式 对所有的 p, q和 r,有 d(p, r) <=d(p, q) + d(q, r).
其中d(p, q)是点(数据对象) p 和 q的距离(相异性)
满足以上三个性质的距离称为度量
相似度的共有性质
1.仅当p = q 时,s(p, q) = 1 (或最大相似度).
2.对所有的p 和 q, s(p, q) = s(q, p). (对称性)
其中s(p, q)是点(数据对象) p 和 q的相似度。
相关性:相关性是对象属性之间线性关系的度量



