会员
周边
新闻
博问
闪存
众包
赞助商
Chat2DB
所有博客
当前博客
我的博客
我的园子
账号设置
会员中心
简洁模式
...
退出登录
注册
登录
RES-HON
博客园
首页
新随笔
联系
订阅
管理
2025年6月4日
飞行动力学
摘要: 飞行动力学 \[\frac{x'_{np}}{\bar{c}} = \frac{x{np}}{\bar{c}} - V_h \eta_h \frac{a_h}{C_{L\alpha_w}} \tau_e \frac{C_{h\alpha}}{C_{h\delta_e}} \]\[\frac{x'_{
阅读全文
posted @ 2025-06-04 15:36 RES_HON
阅读(29)
评论(0)
推荐(0)
2025年4月9日
第六章-平面问题的直角坐标解答
摘要: 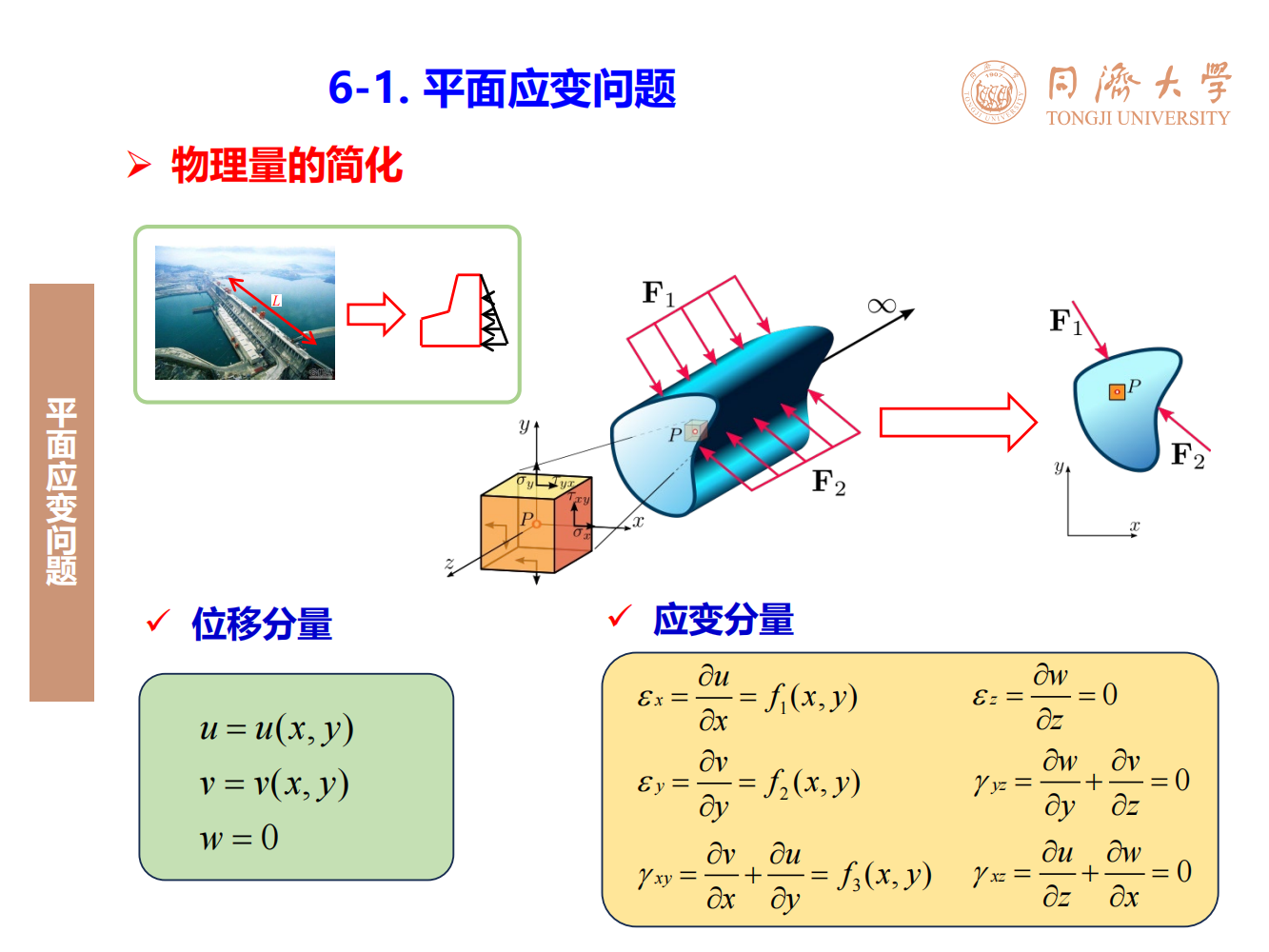 
评论(0)
推荐(0)
2024年12月8日
第9章 组合变形
摘要:  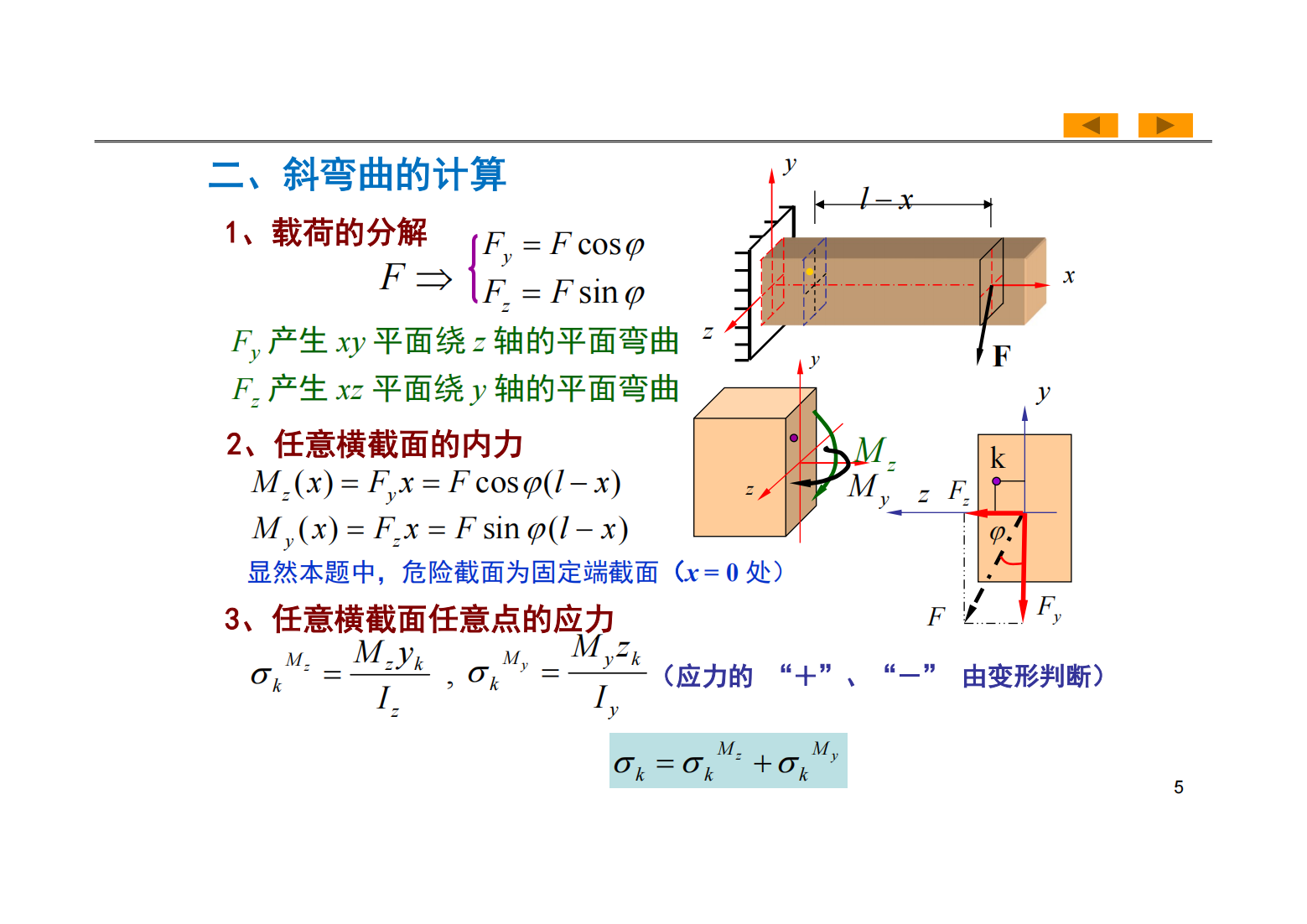  
评论(0)
推荐(0)
2024年12月3日
补充章 平面图形的几何性质
摘要: §A.1静矩和形心 ※定义 图形对x和y轴的静矩 静矩关于 (x) 和 (y) 轴的定义: \[S_y = \int_A x \, dA, \quad S_x = \int_A y \, dA \] 形心公式: \[\bar{x} = \frac{S_y}{A}, \quad \bar{y} = \
阅读全文
posted @ 2024-12-03 21:23 RES_HON
阅读(331)
评论(0)
推荐(0)
2024年12月2日
第8章 应力状态分析 强度理论 精简版
摘要: 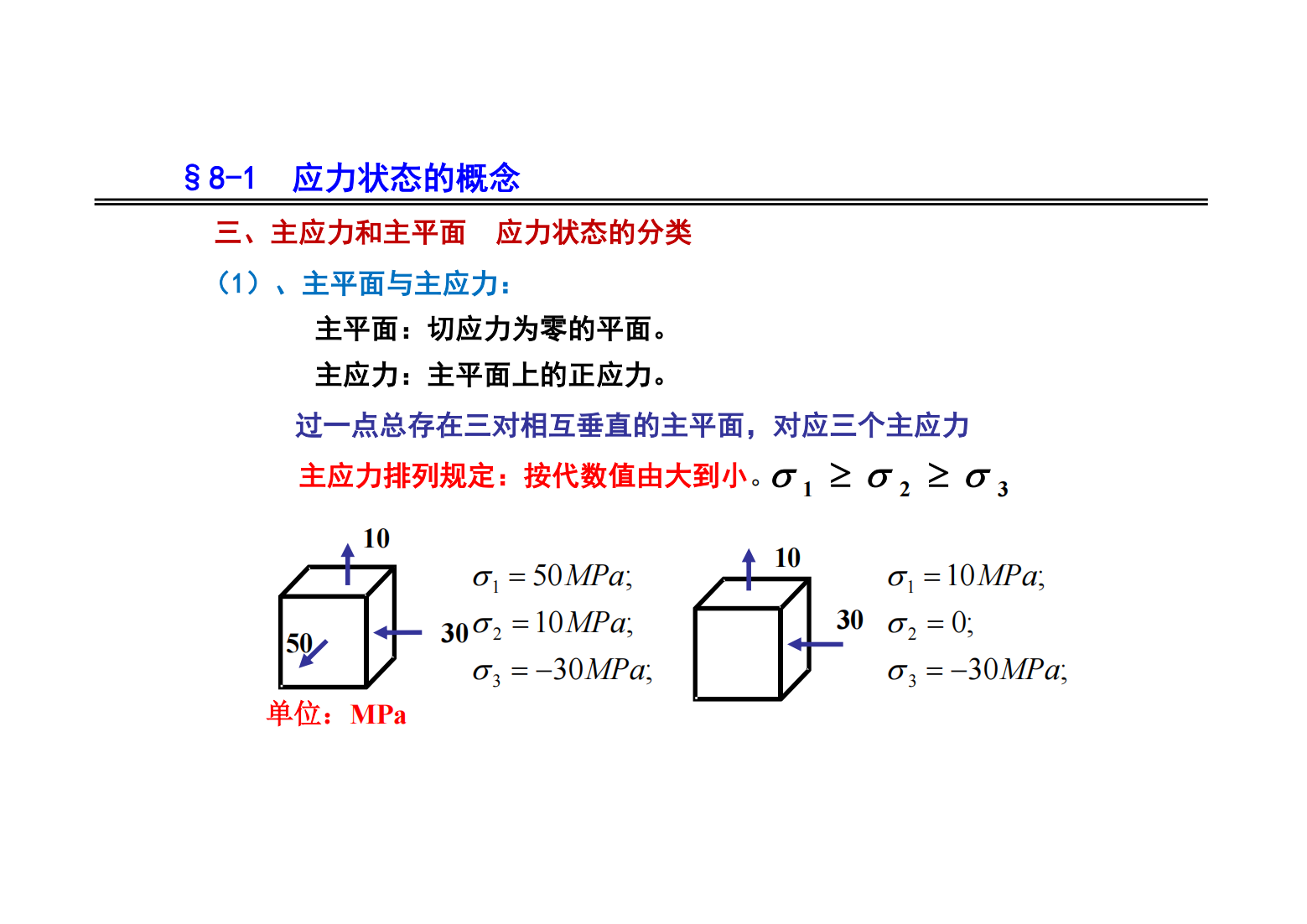 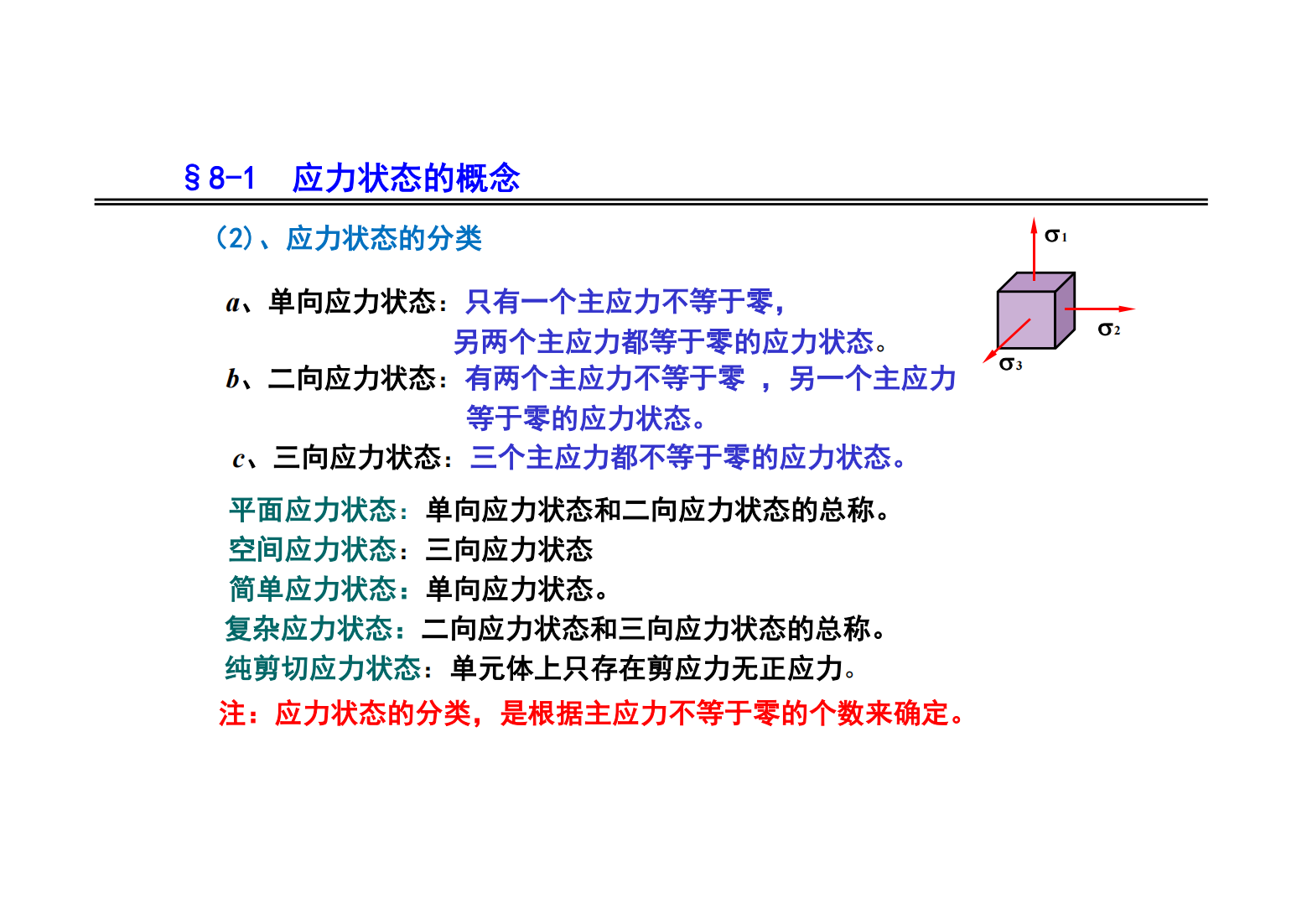  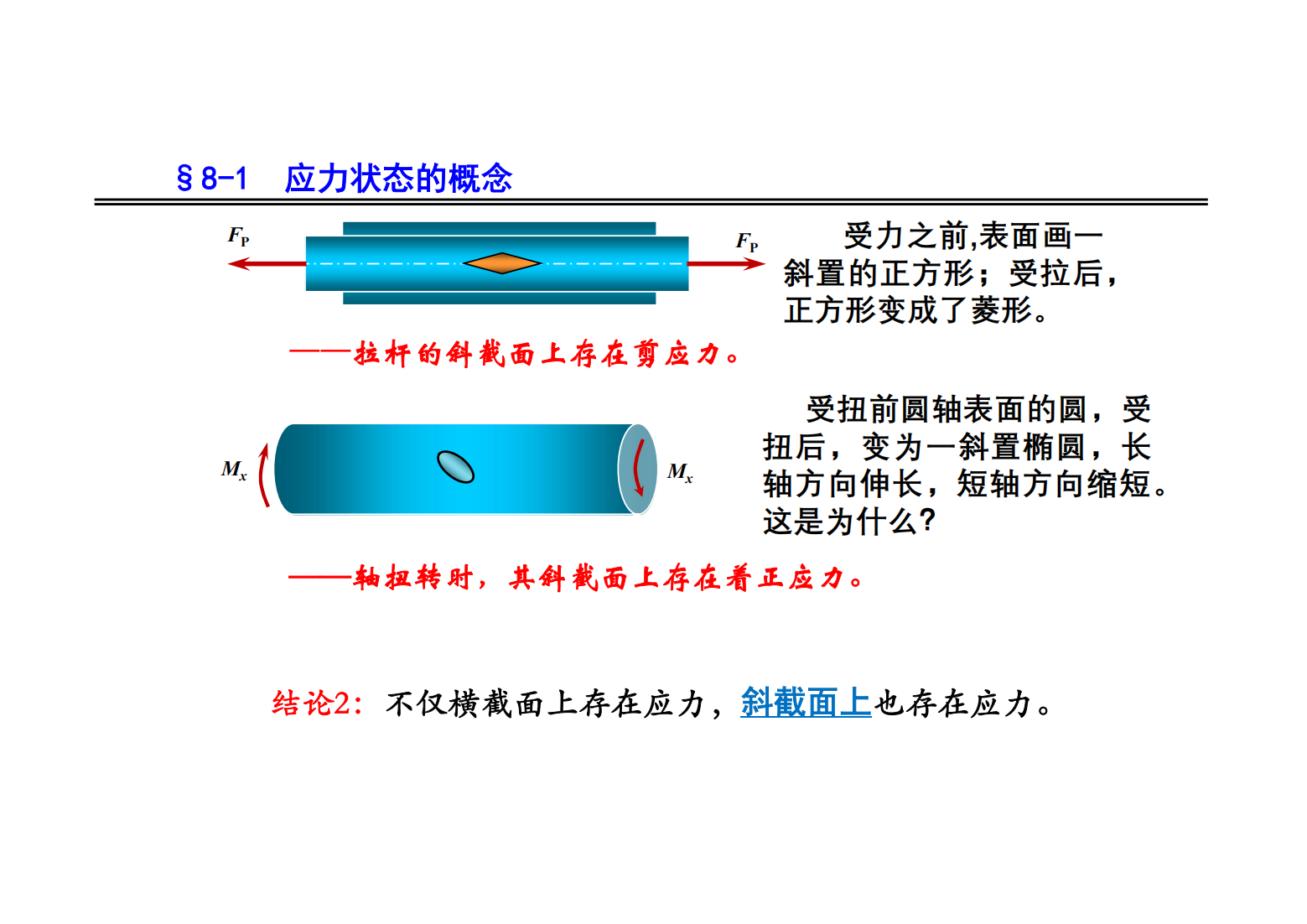 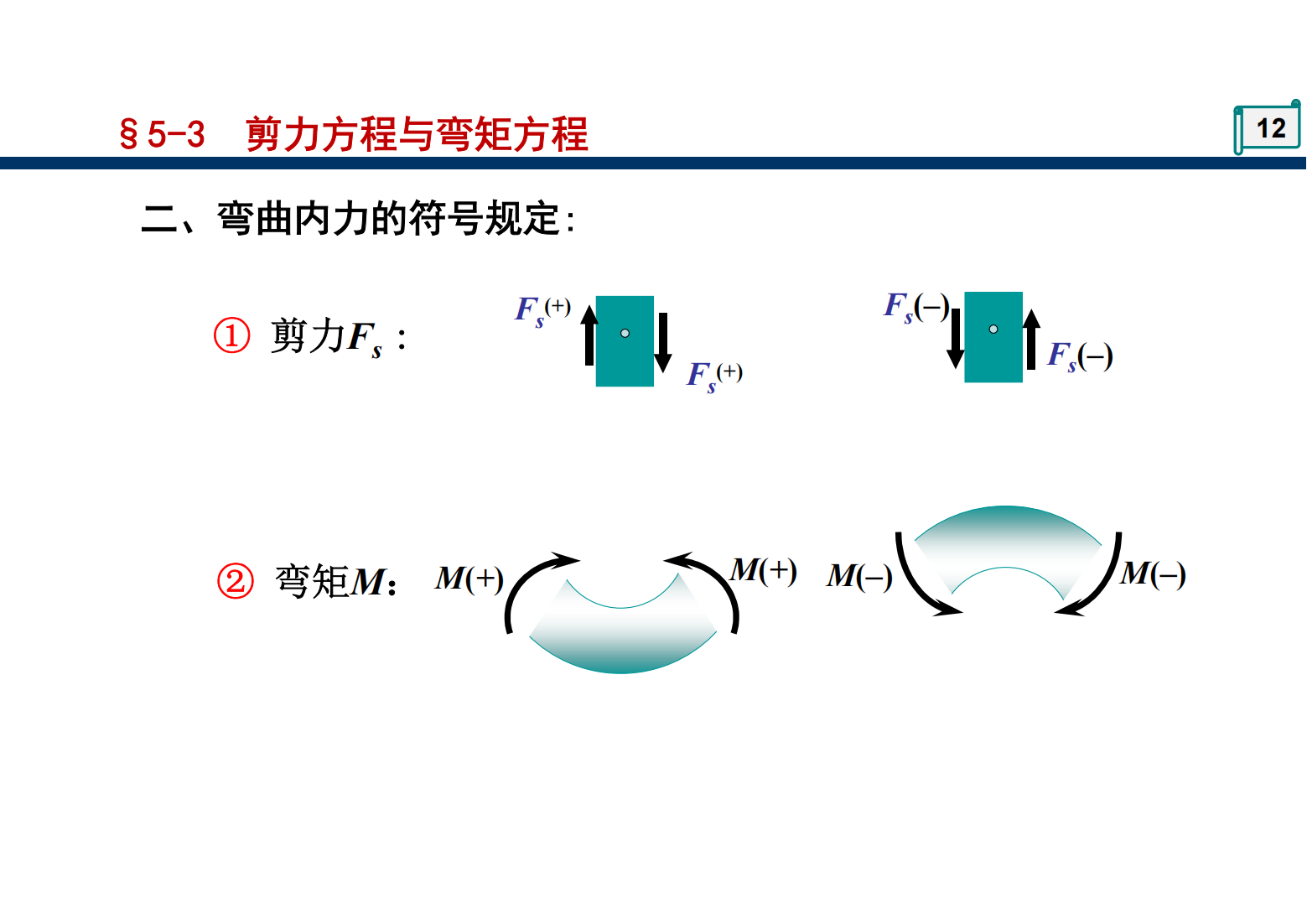 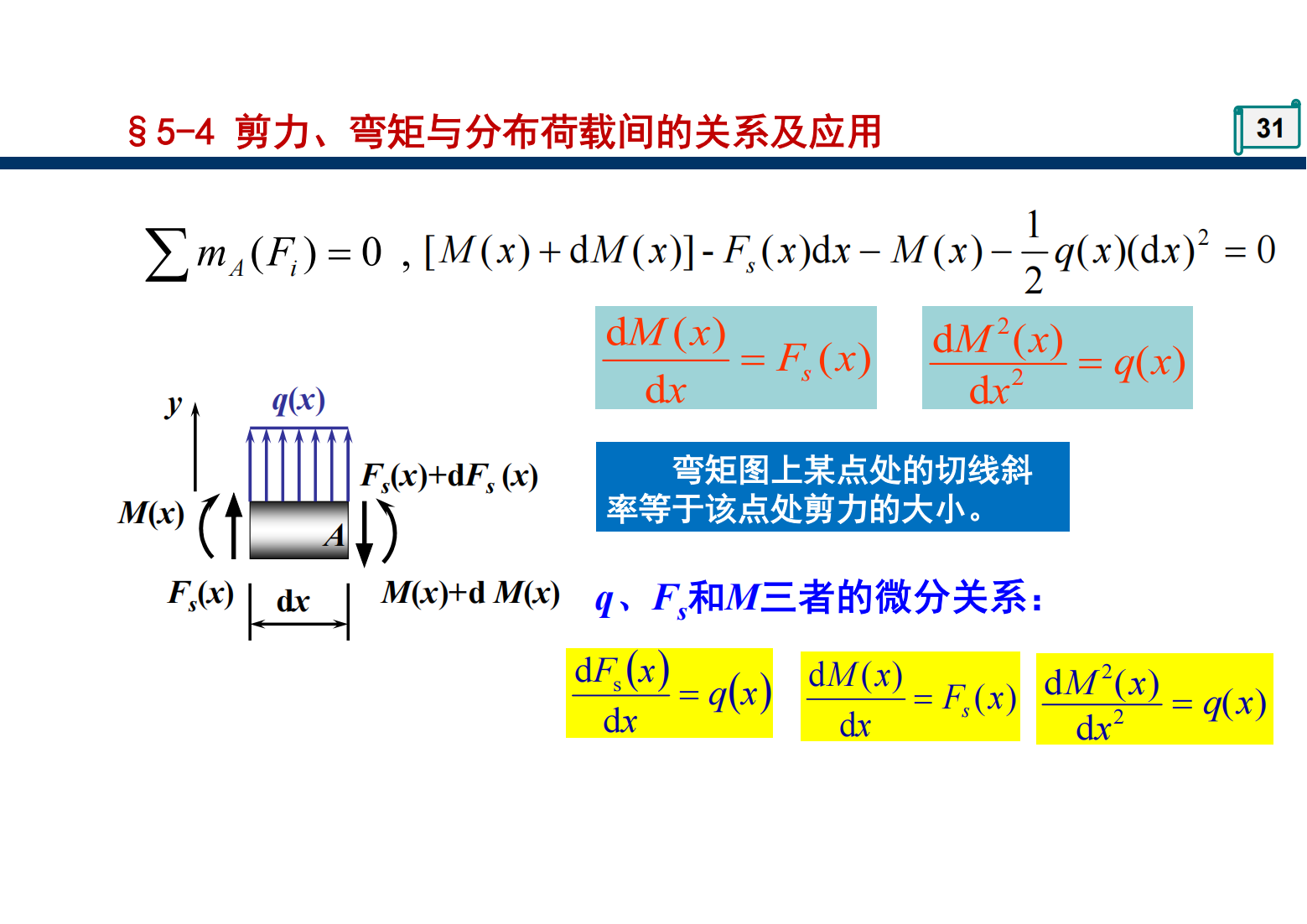   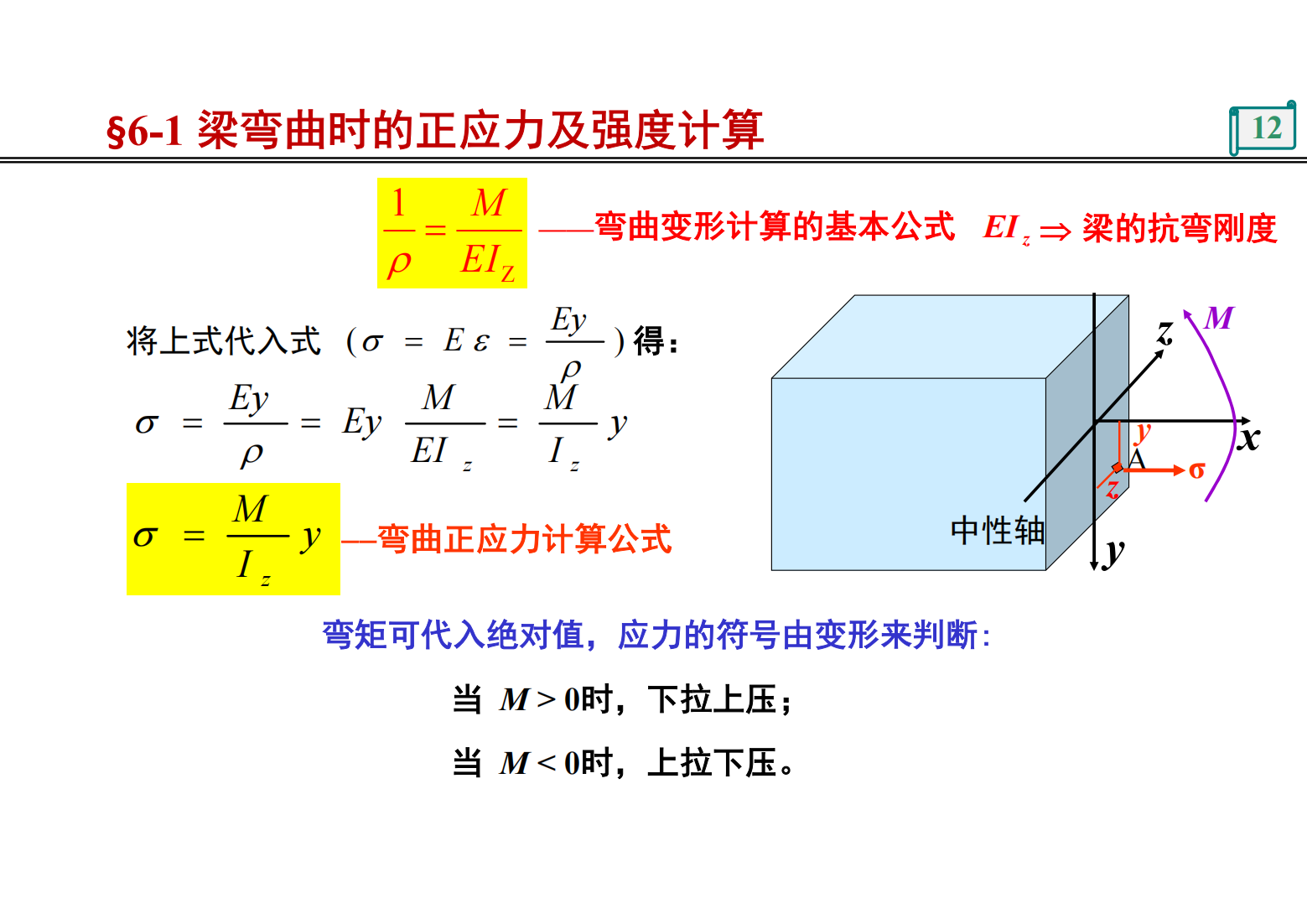 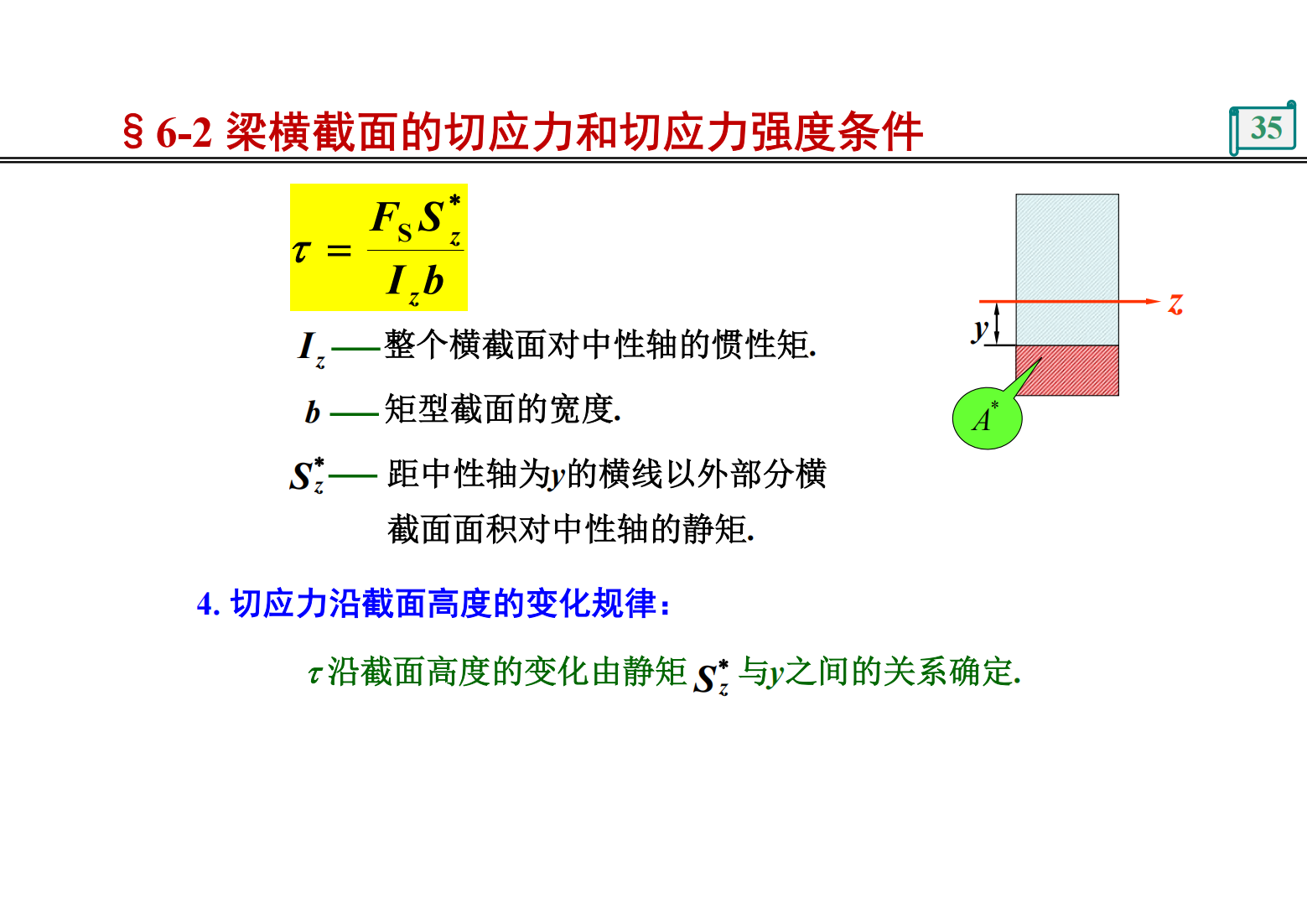 ![第6章 梁的应力 3
阅读全文
posted @ 2024-11-19 08:55 RES_HON
阅读(31)
评论(0)
推荐(0)
下一页
公告