13-傅里叶变换
在学习傅里叶变换的时候,处于一种比较模糊的状态,以下大部分都是转载一位博主的讲解
原文链接:傅里叶分析之掐死教程(完整版)韩昊
| 作 者:韩 昊 |
| 知 乎:Heinrich |
| 微 博:@花生油工人 |
| 知乎专栏:与时间无关的故事 |
| 谨以此文献给大连海事大学的吴楠老师,柳晓鸣老师,王新年老师以及张晶泊老师 |
| 转载的同学请保留上面这句话,谢谢。如果还能保留文章来源就更感激不尽了 |
一、什么是频域
从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为,世间万物都在随着时间不停的改变,并且永远不会静止下来。但如果我告诉你,用另一种方法来观察世界的话,你会发现世界是永恒不变的,你会不会觉得我疯了?我没有疯,这个静止的世界就叫做频域。
先举一个公式上并非很恰当,但意义上再贴切不过的例子:
在你的理解中,一段音乐是什么呢?
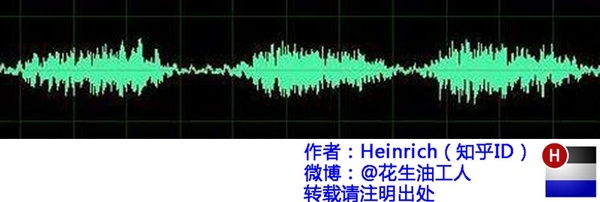
这是我们对音乐最普遍的理解,一个随着时间变化的震动。但我相信对于乐器小能手们来说,音乐更直观的理解是这样的:

所以频域这一概念对大家都从不陌生,只是从来没意识到而已。将以上两图进行简化:
时域(音乐在时域的样子):
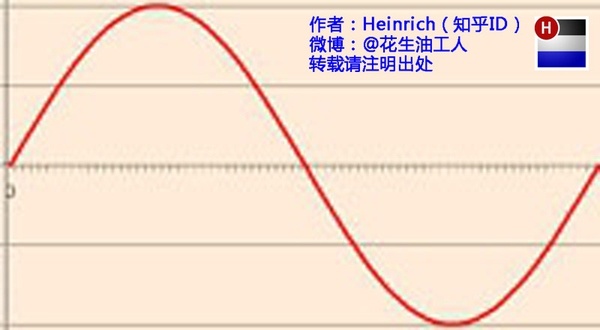
频域(音乐在频域的样子):

在时域,我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势;而在频域,只有那一个永恒的音符。
你眼中看似落叶纷飞变化无常的世界,实际只是躺在上帝怀中一份早已谱好的乐章。

因此,在上述的例子中,我们可以理解为,利用对不同琴键不同力度,不同时间点的敲击,可以组合出任何一首乐曲。
而贯穿时域与频域的方法之一,就是传中说的傅里叶分析。傅里叶分析可分为傅里叶级数(Fourier Serie)和傅里叶变换(Fourier Transformation)
二、傅里叶级数(Fourier Series)的频谱
如果我说我能用前面说的正弦曲线波叠加出一个带 90 度角的矩形波来,你会相信吗?你不会,就像当年的我一样。但是看看下图:
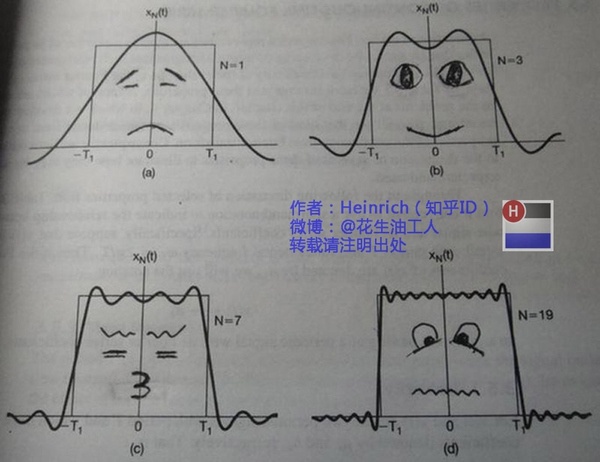
第一幅图是一个郁闷的正弦波 cos(x)
第二幅图是 2 个卖萌的正弦波的叠加 cos (x) +acos (3x)
第三幅图是 4 个发春的正弦波的叠加
第四幅图是 10 个便秘的正弦波的叠加
也就是说,随着正弦波叠加的递增,所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡,而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。一个矩形就这么叠加而成了。但是要多少个正弦波叠加起来才能形成一个标准 90 度角的矩形波呢?不幸的告诉大家,答案是无穷多个(上帝:我能让你们猜着我?)
不仅仅是矩形,你能想到的任何波形都是可以如此方法用正弦波叠加起来的。这是没有接触过傅里叶分析的人在直觉上的第一个难点,但是一旦接受了这样的设定,游戏就开始有意思起来了。
还是上图的正弦波累加成矩形波,我们换一个角度来看看
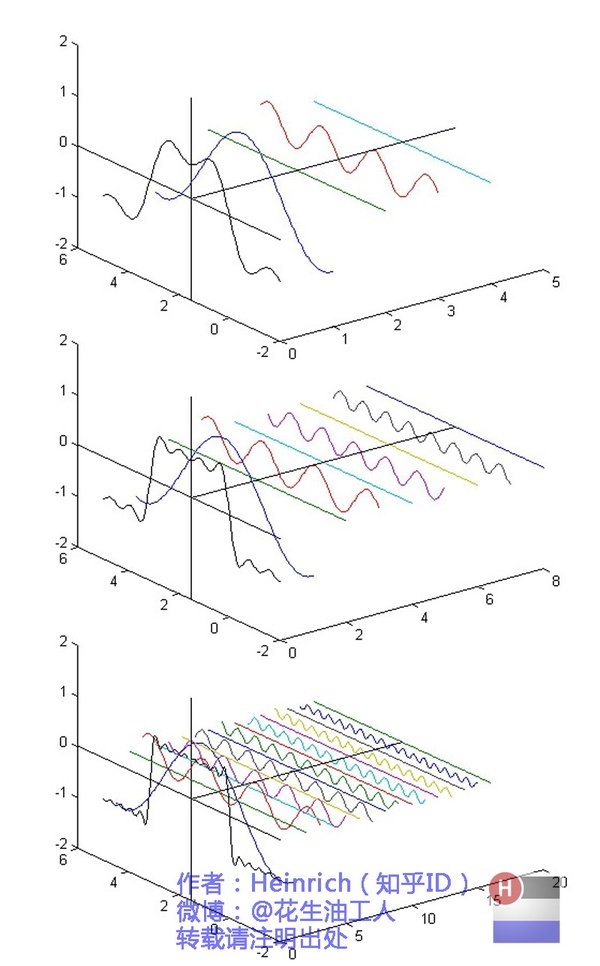
在这几幅图中,最前面黑色的线就是所有正弦波叠加而成的总和,也就是越来越接近矩形波的那个图形。而后面依不同颜色排列而成的正弦波就是组合为矩形波的各个分量。这些正弦波按照频率从低到高从前向后排列开来,而每一个波的振幅都是不同的。一定有细心的读者发现了,每两个正弦波之间都还有一条直线,那并不是分割线,而是振幅为 0 的正弦波!也就是说,为了组成特殊的曲线,有些正弦波成分是不需要的。
回顾一下,之前学习的正弦曲线,y=Asin(ωx+φ)+k
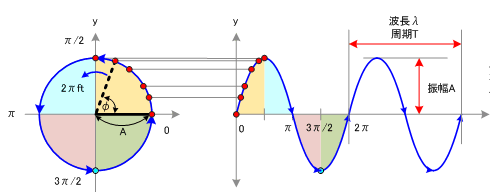
正弦波就是一个圆周运动在一条直线上的投影。所以频域的基本单元也可以理解为一个始终在旋转的圆
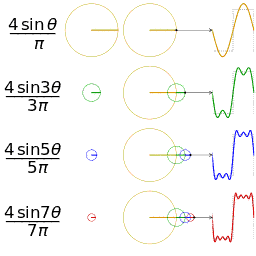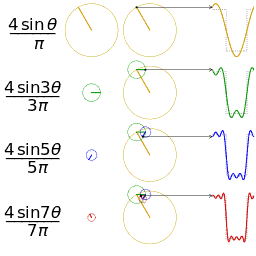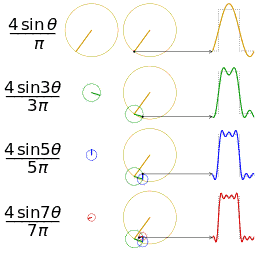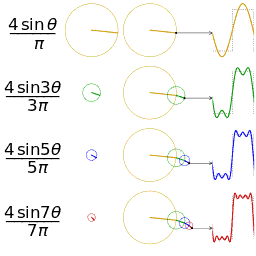
如果我们将一个角频率为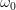 的正弦波 cos(
的正弦波 cos(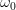 t)看作基础,那么频域的基本单元就是
t)看作基础,那么频域的基本单元就是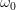 。下图就是矩形波在频域里的样子:
。下图就是矩形波在频域里的样子:
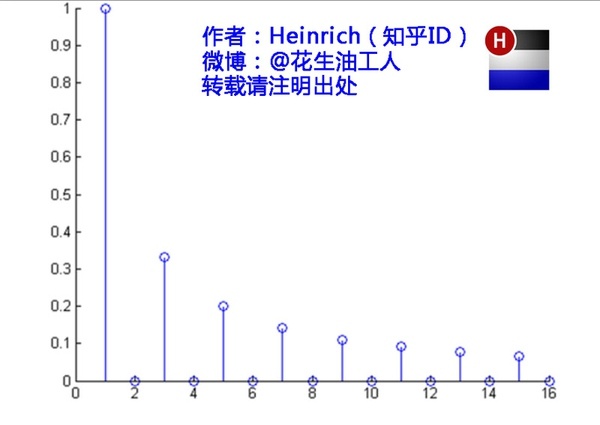
再清楚一点的话
可以发现,在频谱中,偶数项的振幅都是 0,也就对应了图中的彩色直线。也就是振幅为 0 的正弦波。
三、傅里叶级数(Fourier Series)的相位谱
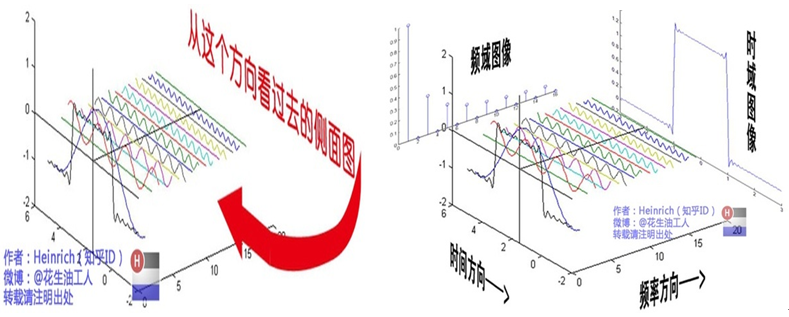
通过时域到频域的变换,我们得到了一个从侧面看的频谱,但是这个频谱并没有包含时域中全部的信息。因为频谱只代表每一个对应的正弦波的振幅是多少,而没有提到相位。基础的正弦波y=Asin(wx+θ)中,振幅,频率,相位缺一不可,不同相位决定了波的位置,所以对于频域分析,仅仅有频谱(振幅谱)是不够的,我们还需要一个相位谱。那么这个相位谱在哪呢?我们看下图,这次为了避免图片太混乱,我们用7个正弦波叠加的图
频谱是从侧面看,相位谱是从下面看
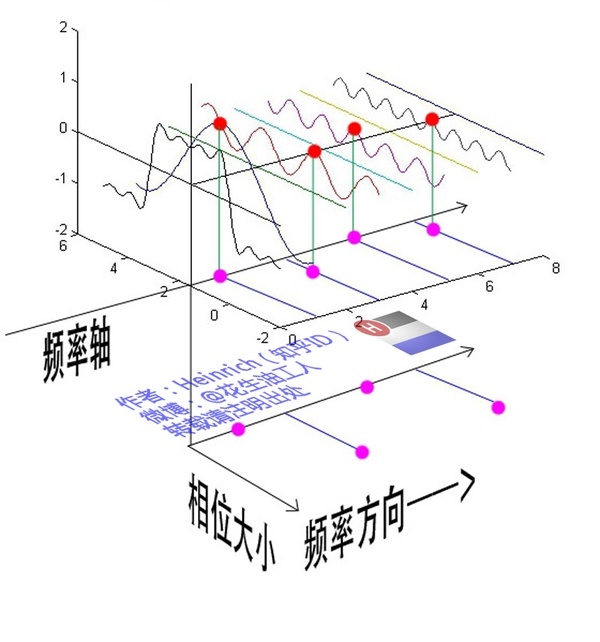
鉴于正弦波是周期的,我们通过图中的小红点来标记正弦波的位置,也就是是距离频率轴最近的波峰。通过将小红点投影到下平面,投影点我们用粉色点来表示。当然,这些粉色的点只标注了波峰距离频率轴的距离,并不是相位。
这里需要纠正一个概念:时间差并不是相位差。在完整的立体图中,我们将投影得到的时间差依次除以所在频率的周期,就得到了最下面的相位谱。
注意到,相位谱中的相位除了0,就是 π。这是因为人为定义相位谱的值域为(-π,π],所以图中的相位差均为π。
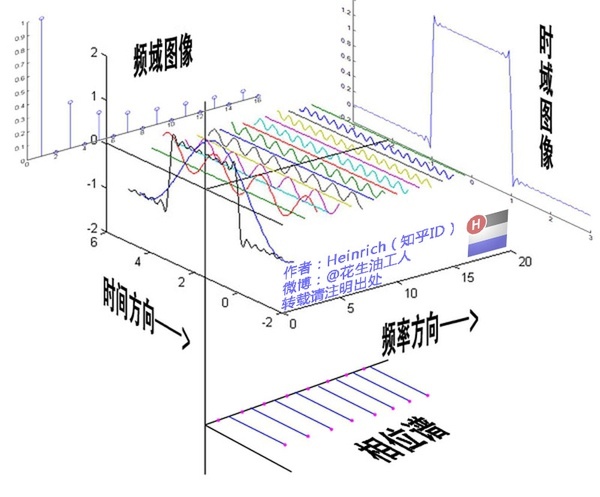
最后来一张时域图像,频域图像和相位谱的大集合:
四、傅里叶变换(Fourier Transformation)
傅里叶级数:在时域是一个周期且连续的函数,转换为一个在频域非周期离散的函数
傅里叶变换:在时域是一个非周期的连续函数,转换为一个在频域非周期的连续函数
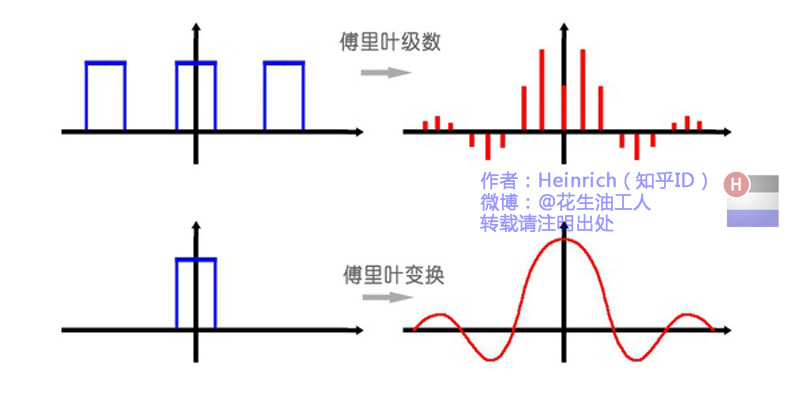
我们也可以换一个角度理解:傅里叶变换实际上是对一个周期无限大的函数进行傅里叶变换,所以傅里叶变换其实是对傅里叶级数的扩展
最后,我们欣赏一下傅里叶变换都能够模拟什么样的波形(以下图片来自:知乎原作者)
如果你觉得傅里叶级数只能用来画心电图,那你就太小看它了,知乎作者甚至可以用它来画恐龙,下面这个图是由50个频率的傅里叶级数组成
画一只可爱的小猫也不是不可以


 浙公网安备 33010602011771号
浙公网安备 33010602011771号