第三课 矩阵和线性代数

SVD 奇异值分解

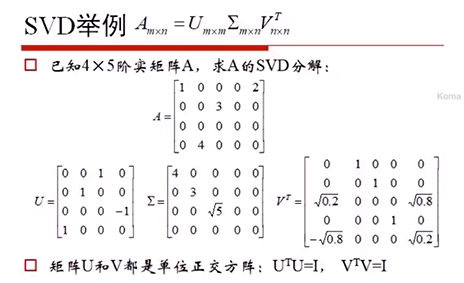
Amxn = Umxm ∑_mxn V_nxn

奇异值分解（Singular Value Decompositionm,简称SVD）是在机器学习领域应用较为广泛的算法之一，也是学习机器学习算法绕不开的基石之一。

奇异值分解（SVD）通俗一点讲就是将一个线性变换分解为两个线性变换，一个线性变换代表旋转，一个线性变换代表拉伸。

注：SVD是将一个矩阵分解成两个正交矩阵和一个对角矩阵，我们知道正交矩阵对应的变换是旋转变换，对角矩阵对应的变换是伸缩变换。

 

 

一、线性代数

定义：方阵的行列式

　　1>1阶方阵的行列式为该元素本身

　　2>n阶方阵的行列式等于它的任一行(或列)的各元素与其对应的代数余子式乘积之和

 

方阵的行列式

　　1>1x1的方阵，其行列式等于该元素本身

　　

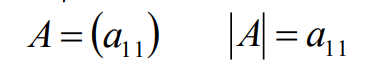
　　2>2x2的方阵，其行列式用主对角线元素乘积减去次对角线元素的乘积

　　

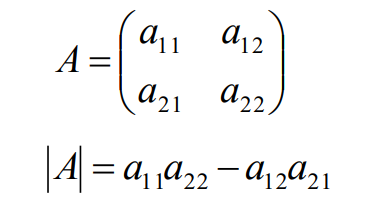
　　3>3x3的方阵

　　

 

代数余子式

　　在n阶行列式中，把(i,j)元素a_ij所在的第i行和第i列划去后，留下来的n-1阶行列式叫做元素a_ij的余子式，记作M_ij

　　代数余子式：

　　　　A_ij = (-1)^i+jM_ij

　　

 

伴随矩阵

　　对于nxn方阵的任意元素a_ij都有各自的代数余子式，A_ij = (-1)^i+jM_ij，

 

 

逆矩阵

　　设A是一个n阶矩阵，若存在另一个n阶矩阵B，使得： AB=BA=E ，则称方阵A可逆，并称方阵B是A的逆矩阵

　　

　　

　　

 

矩阵的乘法

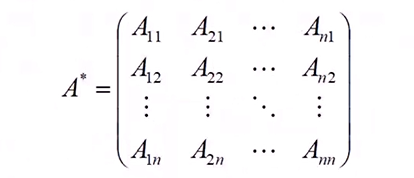
　　矩阵的乘法就是矩阵A的第一行乘以矩阵B的第一列，各个元素对应相乘然后求和作为第一元素的值。

　　矩阵只有当左边矩阵的列数等于右边矩阵的行数时,它们才可以相乘,乘积矩阵的行数等于左边矩阵的行数,乘积矩阵的列数等于右边矩阵的列数 。

　　

　　扩展：矩阵模型

　　

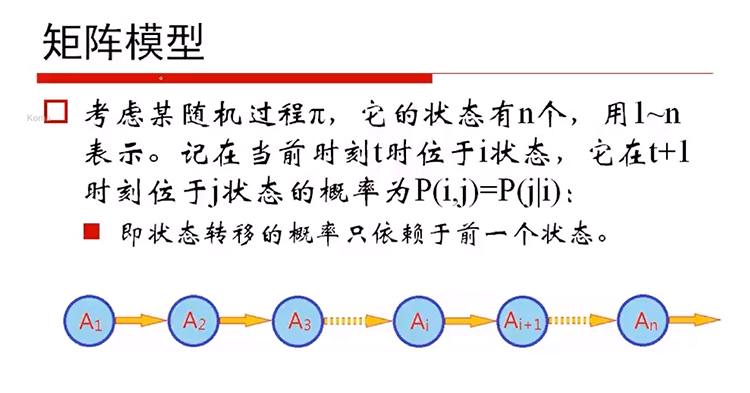
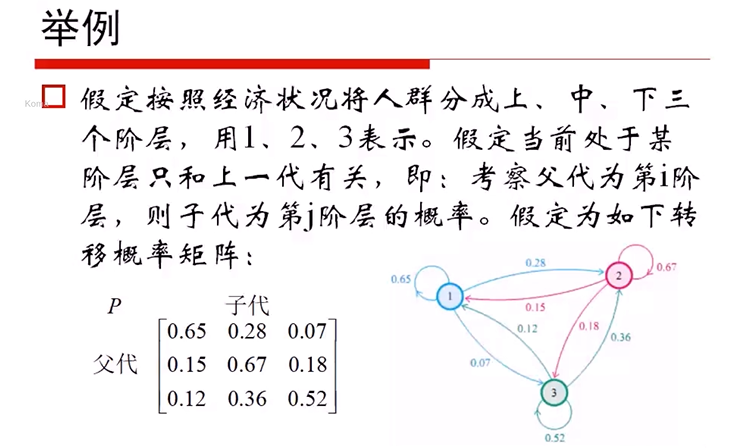
 矩阵和向量的乘法

　　A为mxn的矩阵，X为nx1的列向量，则AX为mx1的列向量

　　

 

矩阵的秩

 

 系数矩阵

 

 

正交阵

　　若n阶矩阵A满足A^TA = I，称A为正交矩阵，简称正交阵

　　　　A是正交阵的充要条件：A的列(行)向量都是单位向量，且两两正交

　　A是正交阵，X为向量，则AX称为正交变换。

　　　　正交变换不改变向量长度

 

二、特征值和特征向量

　　A是n阶矩阵，若数λ和n维非0列向量x满足Ax = λx，那么，

数λ称为A的特征值，x称为A的对应于特征值λ的特征向量

 

　

　　拓展：

　　　　设A为n阶对称阵，则必有正交阵P，使得

　　　　　　P^-1AP = P^TAP = Λ

　　　　1>Λ是以A的n个特征值为对角元的对角阵

　　　　2>该变换称为"合同变换"，A和Λ互为合同矩阵