第二课 概率论
一、概率论
概率论,是研究随机现象数量规律的数学分支。随机现象是相对于决定性现象而言的,在一定条件下必然发生某一结果的现象称为决定性现象

1.古典概型
古典概型也叫传统概率,在这个模型下,随机实验所有可能的结果是有限的,并且每个基本结果发生的概率是相同的。

基本事件总数:
第1个球,有N种放法
第2个球,有N种放法
...
第n 个球,有N种放法
总共有Nn种放法
每个盒子至多放1个球的事件数:
第1个球,有N种放法
第2个球,有N-1种放法
...
第n 个球,有N-n+1种放法
总共有:N(N-1)(N-2)...(N-n+1) = Pn(N)
因此,得出结果:
P(A) = Pn(N)/Nn
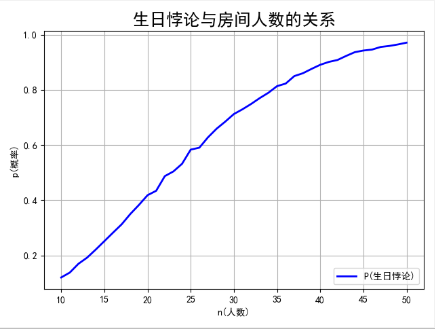
实例:输出在10000例随机样本数量下,n个人中至少两个人生日相同的概率。
""" 生日悖论 生日悖论是指在不少于 23 个人中至少有两人生日相同的概率大于 50%。 例如在一个 30 人的小学班级中,存在两人生日相同的概率为 70%。对于 60 人的大班,这种概率要大于 99%。 从引起逻辑矛盾的角度来说,生日悖论是一种 “佯谬”。但这个数学事实十分反直觉,故称之为一个悖论。 实例:输出在10000例随机样本数量下,n个人中至少两个人生日相同的概率。 """ import random import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl # 检测birthday中是否有同一天的生日 def same(bir): for i in bir: num = 0 for j in bir: if i == j: num = num + 1 if num > 1: return 1 return 0 # 一个房间里面,人数从[10,50] x = np.linspace(10, 50, 41) y = [] for i in range(10, 51): count = 0 # 输出在10000例随机样本数量下,n个人中至少两个人生日相同的概率。 for j in range(10000): birthday = [] for z in range(i): # 产生随机数 房间里每个人的生日,都是从365天里面随机生成 n = random.randint(1, 365) birthday.append(n) if same(birthday) == 1: # 计数 count += 1 # 得到概率,并添加到列表中 p_birthday = count / 10000 y.append(p_birthday) print("当房间里有{0}人时,至少有两个人生日相同的概率为:{1}".format(i,p_birthday)) # 绘图 # 设置字体为SimHei显示中文 mpl.rcParams["font.sans-serif"] = "SimHei" # 设置字体为SimHei显示中文 mpl.rcParams["axes.unicode_minus"] = False # 设置标题为Taylor展开式的应用 plt.title("生日悖论与房间人数的关系",fontsize=18) # 绘制折线图 plt.plot(x, y, linewidth=2, color="b",label="P(生日悖论)") # 给绘制的折线图图填加上图例(右下方) plt.legend(loc="lower right") # 生成网格 plt.grid(True) # x,y轴标签 plt.xlabel("n(人数)") plt.ylabel("p(概率)") # 展示 plt.show()

2.统计数字概率
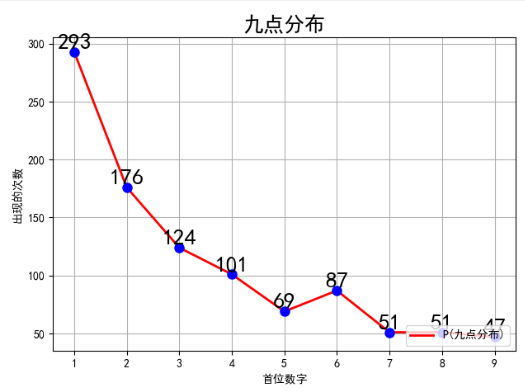
给定某正整数N,统计从1到N的所有数所对应的阶乘中,首位数字出现1的概率
进而,可以计算首位数字是2的概率,是3的概率,从而得到一条"九点分布"
""" 统计数字概率 给定某正整数N,统计从1到N的所有数所对应的阶乘中,首位数字出现1的概率 进而,可以计算首位数字是2的概率,是3的概率,从而得到一条"九点分布" """ import matplotlib as mpl import matplotlib.pyplot as plt def first_digital(x): while x >= 10: x //= 10 return x if __name__ == "__main__": n = 1 frequency = [0] * 9 # <class 'list'> [0, 0, 0, 0, 0, 0, 0, 0, 0] for i in range(1,1000): # i的阶乘 n *= i # 判断i阶乘的首位数字,放进"九点分布"对应的次数 m = first_digital(n) - 1 frequency[m] += 1 print(frequency) # 绘图 # 设置字体为SimHei显示中文 mpl.rcParams["font.sans-serif"] = "SimHei" # 设置字体为SimHei显示中文 mpl.rcParams["axes.unicode_minus"] = False # 设置标题为Taylor展开式的应用 plt.title("九点分布", fontsize=18) x = [1,2,3,4,5,6,7,8,9] y = frequency plt.plot(x,y,"r-",linewidth=2,label="P(九点分布)") plt.plot(x,y,"bo",markersize=8) # 设置数字标签 for a, b in zip(x, y): plt.text(a, b, b, ha="center", va="bottom", fontsize=20) # 给绘制的折线图图填加上图例(右下方) plt.legend(loc="lower right") # 生成网格 plt.grid(True) # x,y轴标签 plt.xlabel("首位数字") plt.ylabel("出现的次数") # 展示 plt.show()
3.本福特定律

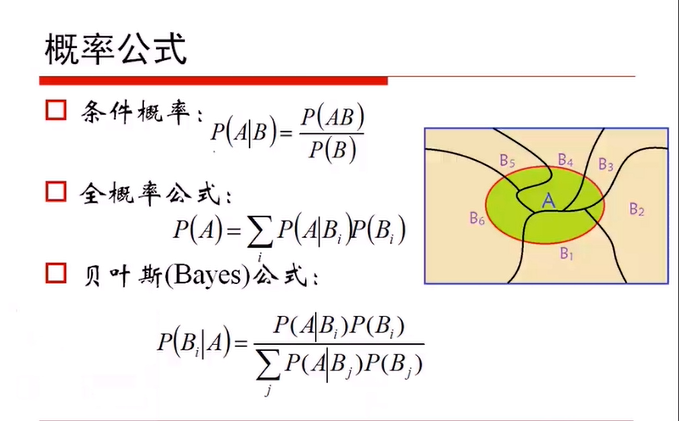
4.概率公式 (贝叶斯公式)


4.分布
1>两点分布

2>两项分布


3>负二项分布

4>泊松分布
在实际事例中,当一个随机事件,以固定的平均瞬时速率λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或者个数就近似地服从泊松分布P(λ)


5>均匀分布

6>指数分布



7>正态分布(重点)

8>Beta分布

5.期望
离散型:E(X) = ∑xipi
连续型:E(X) = ∫xf(x)dx
期望即,概率加权下的"平均值"

6.方差
Var(X) = E(X2) - E2(X)
注意:方差的平方根,称为标准差

7.不相关与独立
1>因为上述定理的保证,使得"不相关"事实上即"二阶独立"
2>即:若X与Y不相关,说明X与Y之间没有线性关系(但有可能存在其它函数关系),不能保证X和Y相互独立
3>但对于二维正态随机变量,X与Y不相关等价于X与Y相互独立
(独立一定不相关,不相关不一定独立)

