第一课 机器学习与数学分析
一、什么是机器学习
对于某给定的任务T,在合理的性能度量方法P的前提下,某计算机程序可以自主学习任务T的经验E;随着提供合适、优质、大量的经验E,该程序对于任务T的性能逐步提高
换句话说:
机器学习是人工智能的一个分支。我们使用计算机设计一个系统,使它能够根据提供的训练数据按照一定的方式来学习;随着训练次数的增加,该系统可以再性能上不断学习和改进;通过参数优化的学习模型,能够用于预测相关问题的输出
1.人类的学习
如何从完全"无知"到掌握知识
语言、颜色、形状等特征统计
有监督学习
学习如何认识月亮(有人教)
无监督学习
从电视上认识"阅兵"(没有人教)
增强学习
走路、踢球
2.机器学习的内涵与外延
机器学习可以解决什么:
给定数据的预测问题
1>数据清洗/特征选择
2>确定算法模型/参数优化
3>结果预测
不能解决什么:
1>大数据存储/并行计算
2>做一个机器人
训练数据
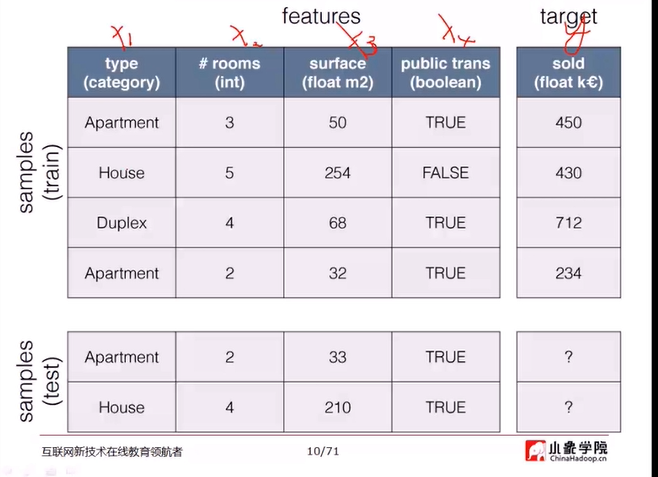
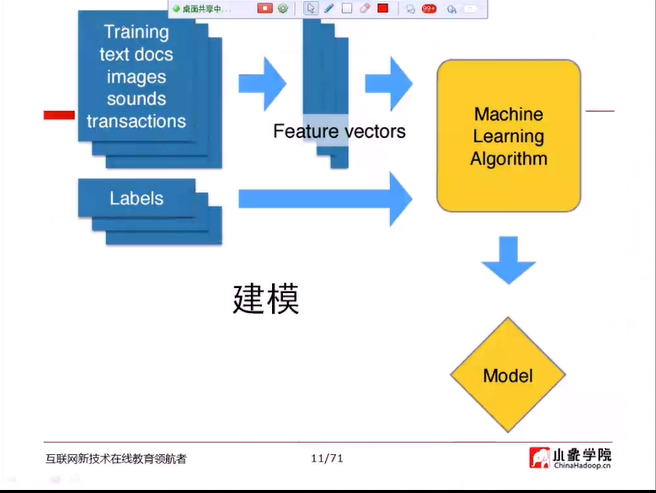
建模的过程
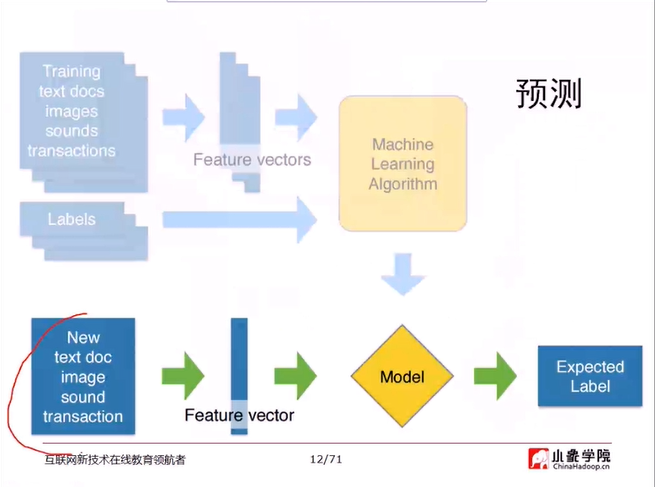
预测的过程
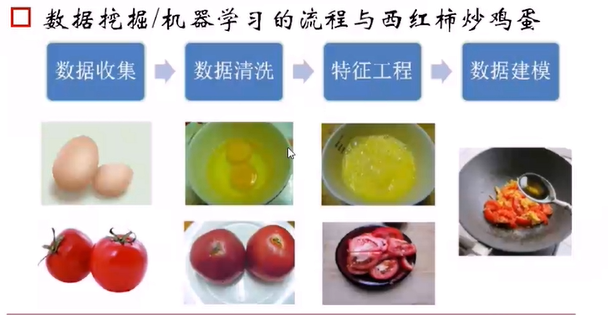
二、机器学习的一般过程
数据收集-->数据清理-->特征工程-->数据建模
实例1
import cmath import matplotlib.pyplot as plt # 测试 if __name__ == "__main__": x = [] y = [] for i in range(1,300): # x 的范围是[0.01,2.99] x.append(float(i)/100) for j in x: # y = ln x y.append(cmath.log(j)) # print(x) # print(y) # 画简单的折线图,同时标注线的颜色、粗细、图例 plt.plot(x,y,"r-",linewidth=3,label="log Curve") a = [x[20],x[175]] b = [y[20],y[175]] plt.plot(a,b,"g-",linewidth=2) # markersize 当前标记的大小 alpha 透明度 plt.plot(a,b,"b*",markersize=15,alpha=0.75) # 给绘制的折线图图填加上图例 plt.legend() # 生成网格 plt.grid(True) # x,y轴标签 plt.xlabel("x") plt.ylabel("log(x)") # 展示 plt.show()
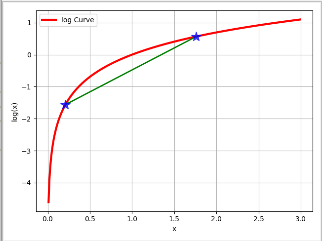
实例2
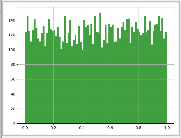
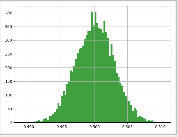
""" 均匀分布的概率密度函数为: p(x) = 1/b−a [a,b)间隔内的任何位置,其他位置为零。 """ import cmath import numpy import matplotlib.pyplot as plt if __name__ == "__main__": # 从均匀分布中抽取样本 low=0.0输出间隔的下边界 high=1.0输出间隔的上限 size= 1000输出形状 # 返回值是numpy.ndarray类型 u = numpy.random.uniform(0.0,1.0,10000) # print("u的类型:{0}\t长度:{1}\t值:{2}".format(type(u), len(u), u)) # 绘制直方图 plt.hist(u,80,facecolor="g",alpha=0.75) # 生成网格 plt.grid(True) # 展示 plt.show() times = 10000 for time in range(times): u += numpy.random.uniform(0.0,1.0,10000) # print("u的类型:{0}\t长度:{1}\t值:{2}".format(type(u), len(u), u)) u /= times # print("u的类型:{0}\t长度:{1}\t值:{2}".format(type(u), len(u), u)) # 绘制直方图 plt.hist(u, 80, facecolor="g", alpha=0.75) # 生成网格 plt.grid(True) # 展示 plt.show()
三、回忆数学知识
1.对数函数
f(x) = logax
当a 不为0时:
loga1 = 0
loga(MN)=logaM+logaN
loga(M/N)=logaM-logaN
logaNn=nlogaN
loge(x)=ln(x)
lg(x)=log10(x)
注意:两个重要的极限定理
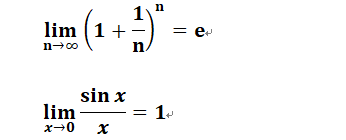
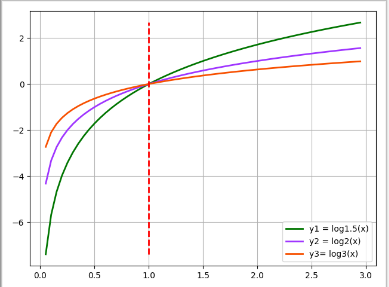
实例3:对数函数的上升速度
y1 = log1.5(x)
y2 = log2(x)
y3 = log3(x)
""" 案例:对数函数的上升速度 """ import cmath import matplotlib.pyplot as plt import numpy if __name__ == "__main__": y1 = [] y2 = [] y3 = [] # 生成数组,[0.05,3),步长为0.05 返回值类型为ndarray x = numpy.arange(0.05,3,0.05) for a in x: # y1 = log1.5(x) a1 = cmath.log(a,1.5) y1.append(a1) # y2 = log2(x) a2 = cmath.log(a, 2) y2.append(a2) # y3= log3(x) a3 = cmath.log(a, 3) y3.append(a3) # 绘制y1 = log1.5(x)的折线图 plt.plot(x, y1, linewidth=2, color="#007500", label="y1 = log1.5(x)") # 绘制y2 = log2(x)的折线图 plt.plot(x, y2, linewidth=2, color="#9F35FF", label="y2 = log2(x)") # 绘制y3= log3(x)的折线图 plt.plot(x, y3, linewidth=2, color="#F75000", label="y3= log3(x)") # 绘制x = 1 的红色虚线 y的值域在[y1[0],y1[-1]] plt.plot([1,1],[y1[0],y1[-1]],"r--",linewidth=2) # 给绘制的折线图图填加上图例(右下方) plt.legend(loc="lower right") # 生成网格 plt.grid(True) # 展示 plt.show()
2.导数
简单的说,导数就是曲线的斜率,是曲线变化快慢的反应
二街导数是斜率变化快慢额反应,表征曲线凹凸性
(xa)'=ax(a-1) a为常数且a≠0
(ax)'=axlna (ex)'=ex
(logax)'=1/(xlna) a>0且 a≠1
(lnx)'=1/x
(sinx)'=cosx (cosx)'=-sinx (tanx)'=(secx)^2 (cotx)'=-(cscx)^2
(secx)'=secxtanx (cscx)'=-csxcotx
(arcsinx)'=1/√(1-x2) (arccosx)'=-1/√(1-x2)
(arctanx)'=1/(1+x2) (arccotx)'=-1/(1+x2)
注意:
常用的三角函数公式:
cos2x+sin2x =1 cos2x-sin2x=cos2x
1-cos2x=2sin2x 1+cos2x=2cos2x
1+tan2x=sec2x 1+cot2x=csc2x
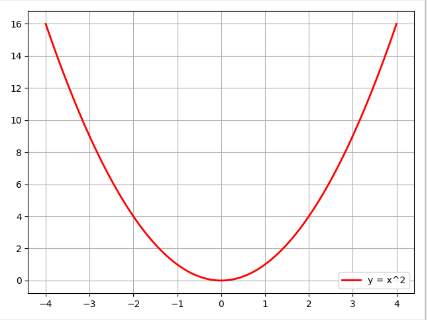
实例4:y = x2
""" 案例:y = x^2 """ import numpy import matplotlib.pyplot as plt if __name__ == "__main__": # 在指定的间隔范围内返回均匀间隔的数字,返回ndarray类型 [-4,4]取一百个 x = numpy.linspace(-4,4,100) y = x ** 2 # 绘制y = x^2 的折线图,红色实线 plt.plot(x, y, "r-", linewidth=2, label="y = x^2") # 给绘制的折线图图填加上图例(右下方) plt.legend(loc="lower right") # 生成网格 plt.grid(True) # 展示 plt.show()
3.积分
∫f(x)dx = F(x) + C
积分是微分的逆运算,即知道了函数的导函数,反求原函数
1>定积分得出的是一个值,定积分的绝对值可以理解为是函数f(x)在坐标轴上的面积
2>不定积分得出的是f(x)的原函数F(x),因为C常数的不同,可以有无数个原函数 F'(X) = f(x)
∫kdx = kx + C (k是常数)
∫xμdx = xμ+1/(μ+1) + C (μ != -1)
∫(1/x)dx = ln|x| + C ∫exdx = ex ∫axdx = ax/lna + C (a>0,且a!=1)
∫cosxdx = sinx + C ∫sinxdx = -cosx + C
∫(secxtanx)dx = secx + C ∫(cscxcotx)dx = -cscx + C
∫(secx)2dx = ∫(1/cos2x)dx = tanx + C ∫(cscx)2dx = ∫(1/sin2x)dx = -cotx + C
∫1/(1+x2)dx = arctanx + C ∫1/(√1-x2)dx = arcsinx + C
扩展:
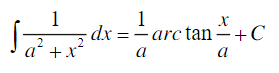
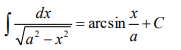
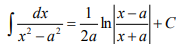
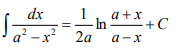
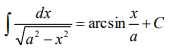
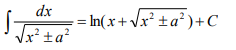
4.泰勒公式

1>泰勒公式的应用---数值计算
初等函数值的计算(在原点展开)
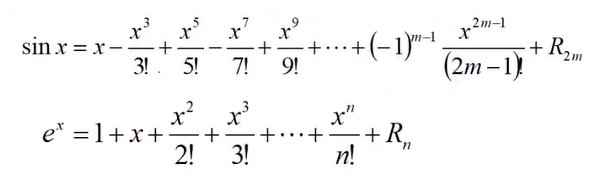
实例:
e^x = 1 + x + x^2/2! +...+ x^n/n! + Rn
""" 泰勒展示的应用 e^x = 1 + x + x^2/2! +...+ x^n/n! + Rn 求整数k和小数r,使得 x = k*ln2 + r |r| <= 0.5*ln2 e^x = e^(k*ln2+r) = e^(k*ln2) * e^r = 2^k * e^r """ import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl import cmath # e^x = 1 + x + x^2/2! +...+ x^10/10! def calc_e_small(x): n = 10 # cumprod() 对给定轴上数组元素的累积乘积 #生成元组[1!,2!,3!,...,10!] f = np.arange(1,n+1).cumprod() #生成元组[x,x^2,x^3,...,x^10] b = np.array([x]*n).cumprod() return 1+np.sum(b / f) # e^x = 2^k * e^r def calc_e(x): reverse = False # 处理负数 exp(-x) = 1/exp(x) if x < 0: x = -x reverse = True ln2 = 0.69314718055994530941723212145818 c = x/ln2 k = int(c+0.5) r = x-k*ln2 #2的k次方乘以e的r次幂 e^x = 2^k * e^r y = (2**k)*calc_e_small(r) if reverse: return 1/y return y if __name__ == '__main__': #-2到0 十个数 在指定的间隔范围内返回均匀间隔的数字 t1 = np.linspace(-2,0,10,endpoint=False) #0到2 二十个数 在指定的间隔范围内返回均匀间隔的数字 t2 = np.linspace(0,2,20) # 沿着现有的轴(t1,t2)连接数组序列 t = np.concatenate((t1,t2)) # 横轴数据 # print("横轴数据为:",t) # empty_like()函数用于创建形状和类型与给定数组相同的新数组 y = np.empty_like(t) # enumerate() 函数用于将一个可遍历的数据对象组合为一个索引序列,同时列出数据和索引下标 for i,x in enumerate(t): y[i] = calc_e(x) print("e^({0}) = {1}\t近似值为:{2}".format(x,y[i],cmath.exp(x))) # 设置字体为SimHei显示中文 mpl.rcParams["font.sans-serif"] = "SimHei" # 设置字体为SimHei显示中文 mpl.rcParams["axes.unicode_minus"] = False # 设置标题为Taylor展开式的应用 plt.title("Taylor展开式的应用", fontsize=18) # 绘制y = e^x 的红色折线图 plt.plot(t, y, "r-", linewidth=2, label="y = e^x") # markersize 当前标记的大小 alpha 透明度 plt.plot(t, y, "b*", markersize=10, alpha=0.75) # x,y轴标签 plt.xlabel('X', fontsize=15) plt.ylabel('exp(X)', fontsize=15) # 给绘制的折线图图填加上图例(右下方) plt.legend(loc="lower right") # 生成网格 plt.grid(True) # 展示 plt.show()

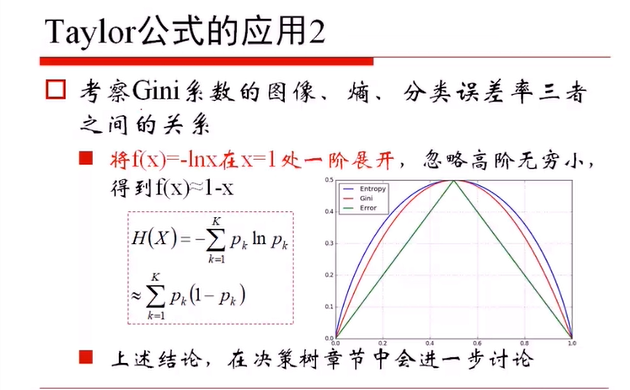
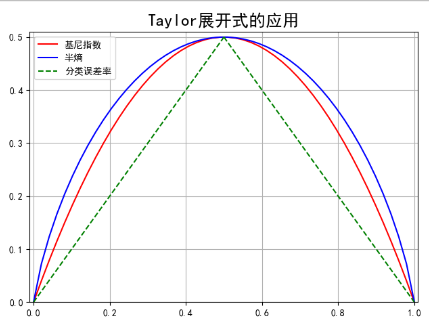
2>泰勒公式的应用---考察Gini系数的图像、熵、分类误差率三者之间的关系
Gini系数:衡量社会贫富差距的物理量
实例:
Gini系数的生成
1>分类问题中,假设有K个类,样本点属于第K类的概率为pk,则概率分布的基尼指数
Gini(p) = ∑pk(1-pk)
2>二类分类问题,若样本点属于第一个类的概率为p,则概率分布的基尼指数
Gini(p) = 2p(1-p)
半熵的生成
entropy(p) = (-∑p*log2p-∑(1-p)*log2(1-p))/2
""" 泰勒展示的应用 Gini系数的生成 1>分类问题中,假设有K个类,样本点属于第K类的概率为pk,则概率分布的基尼指数 Gini(p) = ∑pk(1-pk) 2>二类分类问题,若样本点属于第一个类的概率为p,则概率分布的基尼指数 Gini(p) = 2p(1-p) 半熵的生成 entropy(p) = (-∑p*logp--∑(1-p)*log2(1-p))/2 """ import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl if __name__ == "__main__": # 在指定的间隔范围内返回均匀间隔的数字,返回ndarray类型 [0.0001,0.9999]取五十个 p = np.linspace(0.0001, 0.9999, 50) # Gini系数 Gini(p) = 2p(1-p) Gini = 2 * p * (1-p) # 半熵 Entropy(p) = -∑pi*logpi entropy = (-p * np.log2(p) - (1 - p) * np.log2(1 - p)) / 2.0 # 分类误差 x1 = np.linspace(0, 0.5, 50) y1 = x1 x2 = np.linspace(0.5, 1, 50) y2 = 1 - x2 # 设置字体为SimHei显示中文 mpl.rcParams["font.sans-serif"] = "SimHei" # 设置字体为SimHei显示中文 mpl.rcParams["axes.unicode_minus"] = False # 设置标题为Taylor展开式的应用 plt.title("Taylor展开式的应用", fontsize=18) # 绘制,Gini(p) = 2p(1-p) 红色实线折线图, plt.plot(p, Gini, "r-", label="基尼指数") # 绘制,Entropy(p) = -∑pi*logpi 蓝色实线折线图 plt.plot(p, entropy, "b-", label="半熵") # 绘制,分类误差率折线图 绿色虚线 plt.plot(x1, y1, "g--", label="分类误差率") plt.plot(x2, y2, "g--") # 设置x,y轴的数值显示范围(最大值,最小值) plt.xlim(-0.01, 1.01) plt.ylim(0, 0.51) # 给绘制的折线图图填加上图例(左上角) plt.legend(loc="upper left") # 生成网格 plt.grid(True) # 展示 plt.show()
5.方向导数 与 梯度
方向导数:
本质就是函数在A点无数个切线的斜率的定义。每一个切线都代表一个变化的方向。
(方向导数的本质是一个数值,一个函数沿指定方向的变化率。)
梯度:
函数在A点无数个变化方向中变化最快的那个方向。
(梯度其实是一个向量,一个函数对于其自变量分别求偏导数,这些偏导数所组成的向量就是函数的梯度。)
方向导数与梯度的关系:
函数在某点的梯度是一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。

拓展:
全微分:函数从A点到B点变化的量(其实是取一个无穷小的变化的量)
偏导:多元函数降维时候的变化,比如二元函数固定y,只让x单独变化,从而看成是关于x的一元函数的变化来研究。
导数与微分的区别:
1>导数描述的是函数在一点处的变化快慢的趋势,是一个变化的速率
2>微分描述的是函数从一点(移动一个无穷小量)到另一点的变化幅度,是一个变化的量。


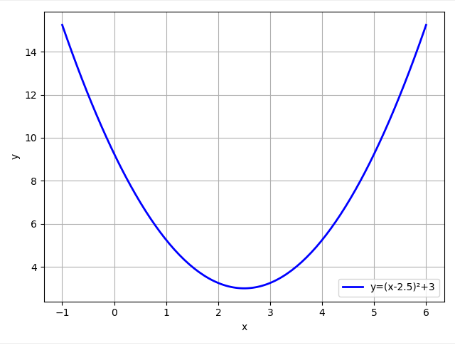
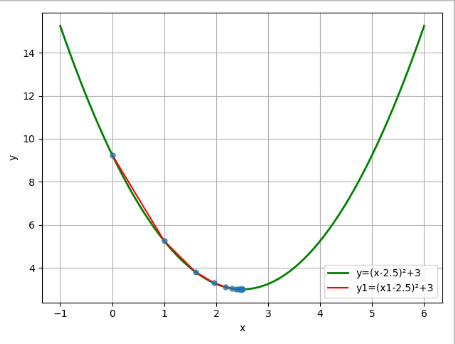
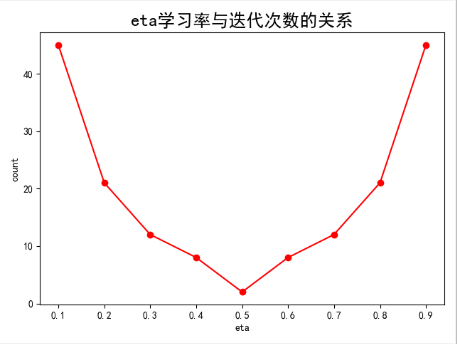
实例:梯度下降法
""" 梯度下降法: 梯度下降法或最速下降法,是求解无约束最优化问题的一种最常用的方法 在机器学习中国,目标函数常常是一个损失函数。 不管怎么称呼,它就是一个函数 f(x),而梯度下降法的目的就是获取这个函数的极小值。 梯度下降法的思想: 就是选取适当的初值 x0,不断迭代更新 x 的值,极小化目标函数,最终收敛。 由于负梯度方向是使函数值下降最快的方向,因此梯度下降在每一步采用负梯度方向更新 x 的值,最终达到函数值最小。 实例: 1>自定义一个可微并且存在最小值的一元函数,用梯度下降法求其最小值。 2>并绘制出学习率从0.1到0.9(步长0.1)时,达到最小值时所迭代的次数的关系曲线,根据该曲线给出简单的分析 """ import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl # -1到6 一百五十个数 在指定的间隔范围内返回均匀间隔的数字 plot_x = np.linspace(-1, 6, 150) # # 同时根据plot_x来生成plot_y y=(x-2.5)²+3 plot_y = (plot_x - 2.5) ** 2 + 3 # 绘制y=(x-2.5)²+3的蓝色折线图 plt.plot(plot_x, plot_y, linewidth=2, color="b", label="y=(x-2.5)²+3") # 给绘制的折线图图填加上图例(右下方) plt.legend(loc="lower right") # 生成网格 plt.grid(True) # x,y轴标签 plt.xlabel("x") plt.ylabel("y") # 展示 plt.show() # 定义一个函数,对函数y=(x-2.5)²+3求导 def fun_Derivative(x): return 2 * (x - 2.5) # 定义一个函数,求函数y=(x-2.5)²+3的值 def fun_value(x): try: return (x - 2.5) ** 2 + 3 except: # 返回一个 负无穷 float("-inf") return float("inf") if __name__ == "__main__": # 随机选取一个起始点 x = 0.0 # eta是学习率,用来控制步长的大小 eta = 0.2 # 用来判断是否到达二次函数的最小值点的条件 (1e-8 科学计数法,1乘以10的-8次方) epsilon = 1e-8 # 用来记录使用梯度下降法走过的点的X坐标 history_x = [x] count = 0 min = 0 while True: # 梯度(导数) gradient = fun_Derivative(x) last_x = x x = x - eta * gradient history_x.append(x) count = count + 1 # 用来判断是否逼近最低点 abs()绝对值 if (abs(fun_value(last_x) - fun_value(x)) < epsilon): min = x break # 绘制y=(x-2.5)²+3的绿色折线图 x属于[-1,6] plt.plot(plot_x, plot_y, linewidth=2, color="g", label="y=(x-2.5)²+3") # 绘制x的轨迹 x1 = np.array(history_x) y1 = fun_value(np.array(history_x)) # print("x1 = ",x1) # print("y1 = ",y1) # 绘制y1=(x1-2.5)²+3的红色折线图 x1属于[0,极值点] plt.plot(x1, y1, color='r',label="y1=(x1-2.5)²+3") # markersize 当前标记的大小 alpha 透明度 plt.plot(x1, y1, ".", markersize=10, alpha=0.75) # 给绘制的折线图图填加上图例(右下方) plt.legend(loc="lower right") # 生成网格 plt.grid(True) # x,y轴标签 plt.xlabel("x") plt.ylabel("y") # 展示 plt.show() # 打印,当eta学习率为0.2到达最低点时,x和y的值 print("当eta学习率为0.2,到达最低点时:min_x = {0}\tmin_y = {1}\t迭代次数:{2}".format(min,fun_value(min),count)) # print("min_x = ",min) # print("min_y = ", fun_value(min)) # print("count = ",count) # 通过改变eta学习率,记录到达最低点时的迭代次数 sum_eta = [] result_count = [] for i in range(1, 10): # 随机选取一个起始点 x = 0.0 # 改变eta是学习率,添加到列表中 eta = i * 0.1 sum_eta.append(eta) # 用来判断是否到达二次函数的最小值点的条件 (1e-8 科学计数法,1乘以10的-8次方) epsilon = 1e-8 num = 0 min = 0 while True: # 梯度(导数) gradient = fun_Derivative(x) last_x = x x = x - eta * gradient num = num + 1 # 用来判断是否逼近最低点 abs()绝对值 if (abs(fun_value(last_x) - fun_value(x)) < epsilon): min = x # break只能退出一层循环,也就是while循环 break result_count.append(num) # 记录学习率从0.1到0.9(步长0.1)时,达到最小值时所迭代的次数 # 设置字体为SimHei显示中文 mpl.rcParams["font.sans-serif"] = "SimHei" # 设置字体为SimHei显示中文 mpl.rcParams["axes.unicode_minus"] = False # 设置标题为Taylor展开式的应用 plt.title("eta学习率与迭代次数的关系",fontsize=18) # 绘制散点图,eta学习率与迭代次数关系的散点图 plt.scatter(sum_eta, result_count, c='r') # 绘制折线图,根据上面散点图绘制折线图 plt.plot(sum_eta, result_count, c='r') # x,y轴标签 plt.xlabel("eta") plt.ylabel("count") plt.show() print(result_count)