DBMS-关系数据库的设计：范式、函数依赖、分解算法、多值依赖
好的关系设计的特点
1. 设计选择：更大的模式
e.g.
instructor (ID, name, dept_name, salary)
department (dept_name, building, budget)
假设用更大的模式（instructor和department自然连接的结果）inst_dept (ID, name, salary, dept_name, building, budget)代替instructor和department，则：某些查询可以用更少的连接来表达；
但相比原设计将会重复存储building和budget，并且承担产生不一致的风险；
无法直接表示关于一个department的信息，除非该department在学校中至少有一位instructor，或将不得不创建带空值的元组。
2. 设计选择：更小的模式
函数依赖（function dependency）：可提供信息以发现“模式可能存在信息重复的问题”的规则。设计者从而可以发现一个模式应该分解成两个或多个模式。
e.g.
假设原有模式inst_dept；
通过对企业本身规则的了解，我们发现大学每个department（由dept_name唯一标识）必须只有一个building和一个budget，得到函数依赖dept_name→budget；
该规则定义：如果存在模式(dept_name, budget)，则dept_name可作为主码（i.e. dept_name的每个特定值对应至多一个budget）；
因为dept_name不能是inst_dept的主码，所以budget可能会重复；
设计者将模式inst_dept分解为模式instructor和模式department。
并非所有的模式分解都有益，应避免有损分解。
e.g.
employee (ID, name, street, city, salary)
假设分解为模式employee1 (ID, name)和employee2 (name, street, city, salary)。自然连接后虽然拥有较多元组，但实际上拥有较少信息（能够指出某个steet, city和salary信息属于一个name为Kim的人，但无法区分是拿一个Kim），造成有损分解。
原子域和第一范式
在关系模型中，如果一个域的元素被认为是不可分的单元，则该域是原子的（atomic）。
如果一个关系模式R的所有属性的域都是原子的，则称R属于第一范式（First Normal Form, 1NF）。
使用函数依赖进行分解
1. 码和函数依赖
合法实例（legal instance）：一个满足所有现实世界约束的实例称为关系的合法实例。在一个数据库的合法实例中所有关系实例都是合法实例。
常用的现实世界约束可形式化地表示为码或函数依赖。
超码（superkey）：考虑关系模式r(R)，R为一个属性集，K为R的子集。如果在关系r(R)的任意合法实例中，对于r的实例中的所有元组对t1和t2总满足“若t1≠t2，则t1[K]≠t2[K]”（i.e. 在关系r(R)的任意合法实例中没有两条元组在R的子集K上可能具有相同的值），则属性集K为r(R)的超码。
函数依赖：考虑关系模式r(R)，属性集α⊆R，属性集β⊆R。
如果对于给定一个r(R)的实例中所有元组对t1和t2总满足“若t1[α]=t2[α]，则t1[β]=t2[β]”，则这个实例满足（satisfy）函数依赖α→β。
如果在r(R)的每个合法实例都满足函数依赖α→β，则该函数依赖在模式r(R)上成立（hold）。
如果函数依赖K→R在r(R)上成立，则K是r(R)的一个超码。
如果一个函数依赖在所有关系中都满足，则称为平凡的（trivial）。一般地，如果β⊆α，则形如α→β的函数依赖是平凡的。
给定关系r(R)上成立的函数依赖集F，有可能会推断出某些其他的函数依赖也一定在该关系上成立。
e.g.
给定模式r(A, B, C)，如果函数依赖A→B和B→C在r上成立，可以退出函数依赖A→C也一定在r上成立。
闭包（closure）：使用符号F+表示集合F的闭包，表示能够从给定集合F推导出的所有函数依赖的集合。F+包含F中所有的函数依赖。
2. Boyce-Codd范式
Boyce-Codd范式（Boyce-Codd Normal Form, BCNF）：可消除所有基于函数依赖能够发现的冗余。
考虑具有函数依赖集F的关系模式R，对F+中所有形如α→β的函数依赖(α⊆R且β⊆R)，如果以下至少一项成立：
·α→β是平凡的函数依赖（i.e. β⊆α）；
·α是模式R的一个超码。
则关系模式R属于BCNF。
（判断时，一般找出所有成立的非平凡的函数依赖，如果箭头左侧为模式的超码，则属于BCNF。）
另：可验证，任何只包含两个属性的模式都属于BCNF。
如果构成一个数据库设计的关系模式集中的每个模式都属于BCNF，则这个数据库设计属于BCNF。
判定和分解不属于BCNF模式的一般规则
如果r(R)为不属于BCNF的一个模式，则存在至少一个非平凡函数依赖α→β，其中α不是R的超码。
在设计中用以下两个模式取代R：
·( α ∪ β )
·( R - ( β – α ) )
e.g.
关系模式inst_dept(ID, name, salary, dept_name, building, budget)不属于BCNF，因为函数依赖dept_name→building, budget在inst_dept上成立，但dept_name不是超码；
( α ∪ β ) = (dept_name, building, budget);
( R - ( β – α ) ) = (ID, name, dept_name, salary);
inst_dept(ID, name, salary, dept_name, building, budget)分解为instructor(ID, name, dept_name, salary)和department(dept_name, building, budget)。
当分解不属于BCNF的模式时，产生的模式中可能有一个或多个不属于BCNF，需要进一步分解，最终结果为一个BCNF模式集合。
3. BCNF和保持依赖
如果函数依赖的检验仅需要考虑一个关系就可以完成，那么检查通过该函数依赖表达的一致性约束的开销就很低。所以有些情况下，到BCNF的分解会妨碍对某些函数依赖的高效检查。
e.g.
设实体集instructor、student和depatment由三元联系集dept_advisor关联，从{instructor, student}对到department多对一。
约束“一个student可以对应多个instructor，但对应于一个给定的department最多只有一个instructor”。
即：a. 一个instructor只能对应一个department；b. 对于一个给定的department，一个student可以对应至多一个instructor。
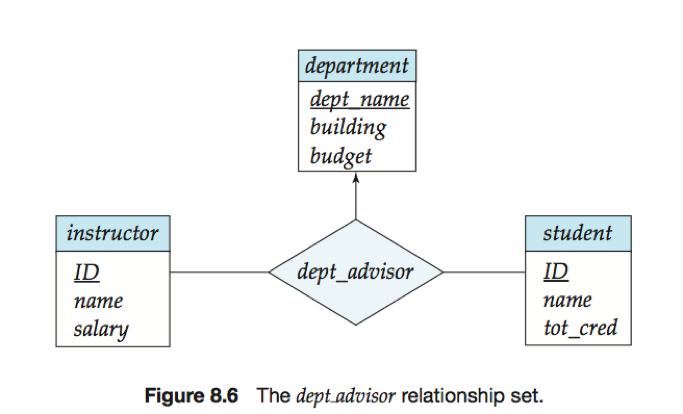
联系集dept_advisor的关系模式为dept_advisor (s_id, i_id, dept_name)。
则：
函数依赖i_ID→dept_name和s_ID, dept_name→i_ID在dept_advisor上成立；
可判断出dept_advisor不属于BCNF，根据BCNF分解规则得到(s_ID, i_ID)和(i_ID, dept_name)；
但在BCNF设计中没有一个模式包含函数依赖s_ID, dept_name→i_ID中出现的所有属性，使得该函数依赖的强制实施在计算上很困难，因此称此BCNF设计不是保持依赖的（dependency preserving）。
当不存在保持依赖的BCNF设计时，必须在BCNF和3NF之间权衡。
4. 第三范式
第三范式（third normal form, 3NF）:如果经常需要保持依赖，可考虑比BCNF弱的第三范式。
考虑具有函数依赖集F的关系模式R，对于F+中所有形如α→β的函数依赖(α⊆R且β⊆R)，如果以下至少一项成立：
·α→β是平凡的函数依赖（i.e. β⊆α）；
·α是模式R的一个超码。
·β - α中的每个属性A都包含于R的一个候选码中。(候选码：最小的超码)(并不要求单个候选码必须包含β- α中的所有属性，β- α中的每个属性都可能包含于不同的候选码中)
则关系模式R属于3NF。
BCNF是比3NF更严格的范式，任何满足BCNF的模式也满足3NF。
e.g.
函数依赖i_ID→dept_name和s_ID, dept_name→i_ID在联系集dept_advisor上成立；
判断后可知函数依赖i_ID→dept_name导致dept_advisor模式不属于BCNF；
β - α = dept_name – i_ID = dept_name；
因为函数依赖s_ID, dept_name→i_ID在dept_advisor上成立，所以dept_name包含于一个候选码中；
dept_advisor属于3NF。
属于3NF的关系也许会含有冗余，但是总存在保持依赖的3NF分解。
5. 更高的范式
某些情况下，使用函数依赖分解模式可能不足以避免不必要的信息重复，因此定义了另外的依赖和范式。
函数依赖理论
1. 函数依赖集的闭包
逻辑蕴含（logically imply）：给定关系模式r(R)，F为r上的函数依赖集，f为R上的函数依赖。如果r(R)的每一个满足F的实例也满足f，则称f被F逻辑蕴含。
可证明，一个关系只要满足给定的函数依赖集F，这个关系也一定满足被F逻辑蕴含的函数依赖f。
令F为一个函数依赖集，F的闭包是被F逻辑蕴含的所有函数依赖的集合，称为F+。给定F，可油函数依赖的形式化定义直接计算出F+。（该运算需要论证，过程比较复杂。）
公理（axiom）：a.k.a. 推理规则，提供一种用于推理函数依赖的更为简单的技术。
Armstrong公理（Armstrong’s axiom）：一组用于寻找逻辑蕴含的函数依赖的规则。通过反复应用这三条规则，可找出给定F的全部F+。
·自反律（reflexivity rule）：给定属性集α和β，若β⊆α，则α→β成立；
·增补律（augmentation rule）：给定属性集α、β和γ，若α→β成立，则γα→γβ成立。(γα表示γ∪α)
·传递律（transitivity rule）：给定属性集α、β和γ，若α→β成立且β→γ成立，则α→γ成立。
Armstrong公理是正确有效的（sound）且完备的（complete）。
为进一步简化计算，可应用另外一些（可用Armstrong公理证明为正确有效的）规则。
·合并律（union rule）：给定属性集α、β和γ，若α→β成立且α→γ成立，则α→βγ成立。
·分解律（decomposition rule）：给定属性集α、β和γ，若α→βγ成立，则α→β成立且α→γ成立。
·伪传递律（pseudotransitivity rule）：给定属性集α、β、γ和δ，若α→β成立且γβ→δ成立，则αγ→δ成立。
使用Armstrong公理计算F+过程的形式化示范：（该过程可以保证终止）
2. 属性集的闭包
给定属性集α和属性B，若α→B，则称B被α函数确定（functionally determine）。
要判断属性集α是否为超码，需要计算函数依赖集F下被α函数确定的所有属性的集合（即α的闭包α+）。可采用两种算法：
a. 计算F+，找出所有左半部为α的函数依赖，并合并这些函数依赖的右半部；（开销很大）
b. 计算属性闭包α+的高效算法，输入F和α，输出result。（该算法可找出a+的全部属性）
属性闭包算法的多种用途：
·判断超码：若检查发现α+包含R中所有属性，则α为超码；
·判断函数依赖成立：若β⊆α+，则函数依赖α→β成立；
·另一种计算F+的方法：对任意γ⊆R，计算出闭包γ+。对任意S⊆γ+，输出函数依赖γ→S。
3. 正则覆盖
数据库系统必须保证更新操作不破坏关系模式上的任何函数依赖，否则必须回滚该更新操作。可通过测试与给定函数依赖集F具有相同闭包的简化集来减小检测冲突的开销。
如果去除函数依赖中的一个属性不改变该函数依赖集的闭包，则称该属性为无关的（extraneous）。
无关属性（extraneous attribute）：
考虑函数依赖集F和F中的函数依赖α→β，
·如果A∈α且F逻辑蕴含(F – {α→β})∪{(α - A)→β}，则属性A在α中是无关的；
·如果A∈β且函数依赖集(F – {α→β})∪{α→(β - A)}逻辑蕴含F，则属性A在β中是无关的。
使用无关属性定义时应注意蕴含的方向，因为(F – {α→β})∪{(α - A)→β}总是逻辑蕴含F，同时F也总是蕴含(F – {α→β})∪{α→(β - A)}。
如何有效检验一个属性是否无关：
设在关系模式R上成立的给定函数依赖集F，考虑依赖α→β中的一个属性A。
·如果A∈β：考虑集合F‘ = (F – {α→β})∪{α→(β - A)}，计算F’下的α+（α的闭包）。如果α+包含A（即α→A能由F‘推出），则A在β中是无关的；
·如果A∈α，令γ = α - {A}，计算F下的γ+（γ的闭包），如果γ+包含β中的所有属性（即γ→β能由F推出），则A在α中是无关的。
正则覆盖（canonical）：F的正则覆盖Fc是一个依赖集，使F逻辑蕴含Fc中的所有依赖，并且Fc蕴含F中的所有依赖。Fc必须具有如下属性：
·Fc中任何函数依赖都不含无关属性；
·Fc中函数依赖的左半部都是唯一的。即：Fc中中不存在两个依赖α1→β1和α2→β2满足α1=α2。
可证明：F的正则覆盖Fc是与F具有相同闭包的最小的简化集，验证是否满足Fc等价于验证是否满足F。
正则覆盖未必是唯一的。
4. 无损分解
无损分解（lossless decomposition）：设关系模式r(R)上的函数依赖集F，令R1和R2为R的分解。如果用两个关系模式r1(R1)和r2(R2)替代r(R)时没有信息损失（即：将r投影至R1和R2上，计算投影结果的自然连接仍得到一样的r），则称该分解为无损分解，a.k.a. 无损连接分解（lossless-join decomposition）。
所有的有效分解都必须是无损的。
有损分解（lossy decomposition）：不是无损分解的分解称为有损分解，a.k.a. 有损连接分解（lossy-join decomposition）。
可用函数依赖来判断分解是否无损。设关系模式r(R)上的函数依赖集F，令R1和R2为R的分解。如果以下函数依赖中至少有一个属于F+（即：R1∩R2是R1或R2的超码）：
·R1∩R2→R1
·R1∩R2→R2
则该分解为无损分解。
5. 保持依赖
限定（restriction）： 设F为关系模式R上的一个函数依赖集，R1, R2, …, Rn为R的一个分解，F在Ri上的限定Fi是F+中所有只包含Ri中属性的函数依赖的集合。因为一个限定中的所有函数依赖只涉及一个关系模式的属性，所以这种函数依赖的检验只需要检查一个关系。
保持依赖的分解（dependency-preserving decomposition）：令F‘ = F1∪F2∪…∪Fn，F’为R上的一个函数依赖集，通常F‘≠F，但有可能F‘+=F+。
如果F’满足F‘+=F+，则F中的所有依赖都被F’逻辑蕴含，证明F‘中的函数依赖满足等价于证明F中的函数依赖满足。
满足F‘+=F+的分解称为保持依赖的分解。
如果分解是保持依赖的，则给定一个数据库更新，所有的函数依赖都可以由单独的关系进行验证，无须计算分解后的关系的连接。
判定保持依赖的算法（需计算F+，开销很大）
输入：分解的关系模式集D={R1, R2, …, Rn}，函数依赖集F。
替代方法1：简单的验证保持依赖的方法
如果F中的每个函数依赖都可以在分解得到的某一个关系上验证，那么这个分解就是保持依赖的；
该方法只能用作一个易于检查的充分条件，如果验证失败也不能判定该分解不是保持依赖的，需进而采用一般化的验证方法。
替代方法2：避免计算F+的验证保持依赖的方法
对F中的每一个α→β执行：
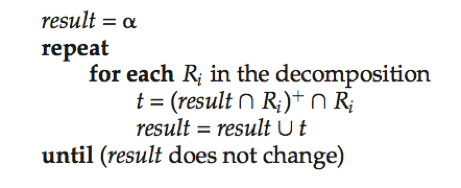
(这里的属性闭包是函数依赖集F下的)如果result包含β中的所有属性，则函数依赖α→β保持。当且仅当F中所有依赖都保持时这个分解是保持依赖的分解。
分解算法
1. BCNF分解
简化的BCNF判定方法
对关系模式R的给定依赖集F中所有函数依赖进行以下检验（不用检查F+中所有的函数依赖）：
·如果α→β是平凡的函数依赖（i.e. β⊆α），则该函数依赖不违反BCNF；
·对非平凡的函数依赖α→β，计算α+，如果α+包含R中所有属性（i.e. α模式R的一个超码），则该函数不违反BCNF。
如果F中没有函数依赖违反BCNF，则关系模式R属于BCNF。
可证明：如果F中没有函数依赖违反BCNF，则F+中也不会函数依赖违反BCNF。
当一个关系分解后，则“仅需检查F中函数依赖，不必检查F+中所有函数依赖”不再适用。可能会有一个属于F+但不属于F的依赖证明分解后的关系不属于BCNF。
对于关系模式R分解后的关系Ri是否属于属于BCNF，应用以下判定：
·对于Ri中属性的每个子集α，确保α+要么不包含Ri - α的任何属性，要么包含Ri的所有属性。
如果Ri上有某个属性集α违反该条件，可证明F+中有函数依赖α→(α+ - α)∩Ri 说明Ri违反BCNF。
BCNF分解算法
如果输入关系模式R不属于BCNF，该算法可将R保持依赖且无损分解成一组BCNF模式。
有些关系不存在保持依赖的BCNF分解。
2. 3NF分解
3NF分解算法
该算法可将输入关系模式R保持依赖且无损分解为一组3NF模式。
生成的模式集可能会包含冗余的模式。如果一个模式Rk包含另一个模式Rj所有的属性，算法会删除Rj，分解仍然是无损的。
一种设计方法：
首先使用3NF算法，然后对3NF设计中任何一个不属于BCNF的模式用BCNF算法分解。如果结果不是保持依赖的，则还原到3NF设计。
3. 3NF算法的正确性
上述3NF分解算法又称3NF合成算法（3NF synthesis algorithm）。
该算法通过保证至少有一个模式包含被分解模式的候选码，确保无损分解。
可证明：如果一个关系Ri在由该算法产生的分解中得到，Ri一定属于3NF。
该算法结果不是唯一确定的，因为：
·一个函数依赖集可能有不止一个正则覆盖，某些情况下该算法的结果依赖于Fc中依赖的顺序；
·该算法有可能分解一个已经属于3NF的关系，但仍然保证分解是属于3NF的。
4. BCNF和3NF的比较
3NF的优点：总能在满足无损并保持依赖的前提下得到3NF设计；
3NF的缺点：可能不得不用空值表示数据项间的某些（可能有意义的）联系，并且存在信息重复问题。
SQL中指定函数依赖的途径较少：
可用断言保证函数依赖（但目前没有数据库系统支持强制实施函数依赖所需的复杂断言，且检查开销大）；
一些特殊的函数依赖可用主码或唯一约束声明超码指定（使用标准SQL只能高效检查左半部是码的函数依赖）。
如果分解不能保持依赖，对函数依赖的检查可能会用到连接。可通过使用物化视图的方法降低开销（如果数据库系统支持物化视图上的主码约束）：
给定一个非保持依赖的BCNF分解，对于正则覆盖Fc中每一个在分解中未保持的依赖α→β，定义一个物化视图对分解中所有关系计算连接，并将结果投影到αβ上。利用约束unique(α)或primary key(α)在物化视图上检查函数依赖。
优点：因为维护物化视图是数据库的工作，应用程序员不需要编码保持冗余数据在更新上的一致性；
缺点：物化视图会带来额外开销；目前绝大多数数据库系统不支持物化视图上的约束。
综上，因为在SQL中检查非主码约束的函数依赖很困难，在不能得到保持依赖的BCNF分解的情况下，通常倾向于选择BCNF。
对应用函数依赖进行数据库设计的目标：1. BCNF 2. 无损 3. 保持依赖
使用多值依赖的分解
1. 多值依赖
函数依赖规定某些元组不能出现在关系中。如果A→B成立，则不能有两个元组在A上值相同而在B上值不同。因此又称相等产生依赖（equality-generating dependency）。
多值依赖并不排除某些元组的存在，而是要求某种形式的其他元组存在于关系中，因此又称元组产生依赖（tuple-generating dependency）。
多值依赖有助于理解并消除某些形式（函数依赖无法理解的）的信息重复。
多值依赖（multivalued dependency）：给定关系模式r(R)，α⊆R且β⊆R，如果在关系r(R)的任意合法实例中，对于r中任意一对满足t1[α]= t2[α]的元组对t1和t1，r中都存在元组t3和t4使得
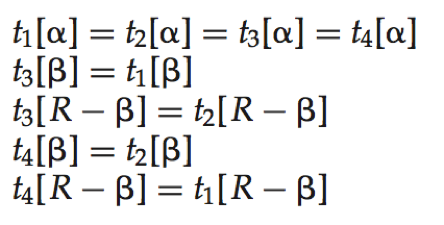
则多值依赖α→→β在R上成立。
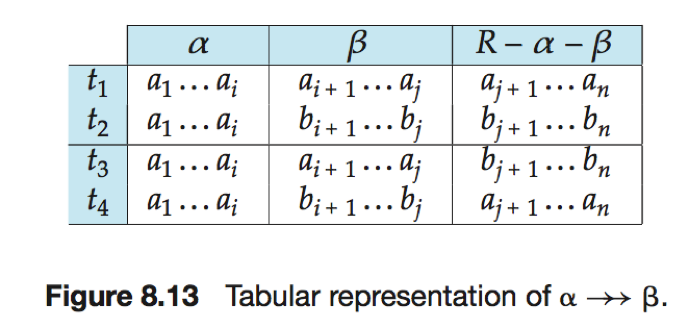
（多值依赖α→→β表明α和β之间的联系独立于α和R-β之间的联系。）
如果模式R上的所有关系都满足多值依赖α→→β，则α→→β是模式R上平凡的多值依赖。
如果β⊆α或β∪α=R，则多值依赖α→→β是平凡的。
多值依赖的两种使用方式
1）检验关系以确定它们在给定的函数依赖集和多值依赖集下是否合法；
2）在合法关系及上指定约束。
如果关系r不满足多值依赖，可通过向r中增加元组构造一个确实满足多值依赖的关系r’。
e.g.
向r2中加入元组(Physics, 22222, Main, Manchester)和(Math, 22222, North, Rye)可使该关系合法化。
用D表示函数依赖和多值依赖的集合， D的闭包D+表示由D逻辑蕴含的所有函数依赖和多值依赖的集合。
可用函数依赖和多值依赖的规范定义根据D计算D+。（适用于处理非常简单的多值依赖）；
可用推理规则系统推导依赖集（适用于复杂的依赖）。对于α、β⊆R，有以下规则：
·若α→β，则α→→β；（每个函数依赖也是一个多值依赖）
·若α→→β，则α→→R-α-β。
2. 第四范式
第四范式（Fourth Normal Form, 4NF）：比BCNF约束更严格，每个4NF模式一定也属于BCNF，但有些BCNF模式不属于4NF。
考虑函数依赖集和多值依赖集为D的关系模式r(R)，α⊆R且β⊆R，对D+中所有形如α→β的多值依赖，如果以下至少有一项成立：
·α→→β是一个平凡的多值依赖；
·α是R的一个超码。
则r(R)属于第四范式。
如果构成一个数据库设计的关系模式集中的每个模式都属于4NF，则该数据库设计属于4NF。
要检验分解中的每一个关系模式ri是否属于4NF，需要找到每一个ri上成立的多值依赖。
限定（restriction）： 设D为关系模式R上的一个函数依赖和多值依赖的集合，R1, R2, …, Rn为R的一个分解，D在Ri上的限定Di包含：
·D+中所有只包含Ri中属性的函数依赖；
·所有形如α→→β∩Ri的多值依赖，其中α⊆Ri且α→→β属于D+。
3. 4NF分解
4NF分解算法（类似BCNF分解算法，但使用多值依赖以及D+在Ri上的限定）
该算法只产生无损分解。
更多的范式
连接依赖（join dependency）：概化了多值依赖的一类约束，并引出了投影-连接范式（Project-Join Normal Form, PJNF, a.k.a. 第五范式 fifth normal form）。
一类更一般化的约束可引出域-码范式（Domain-key Normal Form, DKNF）。
PJNF和DKNF等其他范式消除了更多细微形式的冗余，但难以操作且很少使用。
第二范式（Second Normal Form, 2NF）只具有历史意义。
数据库的设计过程
1. E-R模型和规范化
如果小心定义E-R图并正确识别所有实体，则由E-R图生成的关系模式应该不需要太多进一步的规范化；
一个实体的属性之间有可能存在函数依赖，大多数是由不好的E-R图设计引起的；
包含两个实体集以上的连计息有可能会使产生的模式不属于所期望的范式；
函数依赖有助于检测到不好的E-R设计，如果生成的关系模式不属于想要的范式，可在E-R图中解决（规范化可作为数据建模的一部分规范地进行）。
创建E-R设计的过程倾向于产生4NF设计。如果一个多值依赖成立且不是被相应的函数依赖所隐含的，则通常由a. 一个多对多的联系集 或 b. 实体集的一个多值属性 引起。
2. 属性和联系的命名
唯一角色假设（unique-role assumption）：数据库设计的一个期望的特性，指每个属性名在数据库中只有唯一的含义。（因此不能使用同一个属性在不同的模式中表示不同的东西）
如果不同关系中的属性含义不兼容，适合采用不同的名字；（唯一角色假设）
如果不同关系中的属性有相同的含义，适合采用相同的名字。
习惯上在模式的属性名顺序中将主码属性列在前面；
实体集命名习惯采用单数形式（单数复数形式皆可，所有实体集应保持一致）。
3. 为了性能去规范化
去规范化（denormalization）：把一个规范化的模式编程非规范化的过程，用于调整系统性能以支持响应时间苛刻的操作。
e.g.
可保存一个包含course和prereq所有属性的关系以避免计算连接，提高性能。（代价是用于保持冗余数据一致性的额外工作）；
更好的方法：可使用规范化的模式将course和prereq的连接作为物化视图额外存储。
4. 其他设计问题
时态数据建模
时态数据（temporal data）：具有关联的时间段的数据，在时间段之间数据有效（valid）。
快照（snapshot）：数据的快照表示一个特定事件点上该数据的值。
时态函数依赖（temporal functional dependency）：如果对于关系模式r(R)的所有合法实例，r的所有快照都满足函数依赖X→Y，则时态函数依赖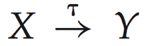
在r(R)上成立。
也可退回到更简单的方法来设计时态数据库：
先设计整个数据库，忽略时态改变（仅考虑一张快照）；
研究多个关系，决定哪些关系需要跟踪时态变化；
将起始时间和终止时间作为属性，为每隔这样的关系添加有效时间；
e.g.
关系模式course(course_id, title, dept_name, start, end)
该关系的一个实例最初含有总共2条记录：
(CS-101, “Introduction to Programming”, 1985-01-01, 2000-12-31)
(CS-101, “Introduction to C”, 2001-01-01, 9999-12-31) //用相当远的终止日期表示当前仍然有效
插入一条新的”Introduction to Java”记录的操作：
将第二条记录的终止时间改为正确有效的终止时间，插入新元组。
如果另一个关系有一个参照时态关系的外码，需决定参照是针对当前版本的数据还是一个特定时间点的数据。
