AI-Knowledge-based agents: propositional logic, propositional theorem proving, propositional model checking, propositional logic agent.
Knowledge-based agents
Intelligent agents need knowledge about the world in order to reach good decisions.
Knowledge is contained in agents in the form of sentences in a knowledge representation language that are stored in a knowledge base.
Knowledge base (KB): a set of sentences, is the central component of a knowledge-based agent. Each sentence is expressed in a language called a knowledge representation language and represents some assertion about the world.
Axiom: Sometimes we dignify a sentence with the name axiom, when the sentence is taken as given without being derived from other sentences.
TELL: The operation to add new sentences to the knowledge base.
ASK: The operation to query what is known.
Inference: Both TELL and ASK may involve, deriving new sentences from old.
The outline of a knowledge-based program:

A knowledge-base agent is composed of a knowledge base and an inference mechanism. It operates by storing sentences about the world in its knowledge base, using the inference mechanism to infer new sentences, and using these sentences to decide what action to take.
The knowledge-based agent is not an arbitrary program for calculating actions, it is amenable to a description at the knowledge level, where we specify only what the agent knows and what its goals are, in order to fix its behavior, the analysis is independent of the implementation level.
Declarative approach: A knowledge-based agent can be built simply by TELLing it what it needs to know. Starting with an empty knowledge base, the gent designer can TELL sentences one by one until the agent knows how to operate in its environment.
Procedure approach: encodes desired behaviors directly as program code.
A successful agent often combines both declarative and procedural elements in its design.
A fundamental property of logical reasoning: The conclusion is guaranteed to be correct if the available information is correct.
Logic
A representation language is defined by its syntax, which specifies the structure of sentences, and its semantics, which defines the truth of each sentence in each possible world or model.
Syntax: The sentences in KB are expressed according to the syntax of the representation language, which specifies all the sentences that are well formed.
Semantics: The semantics defines the truth of each sentence with respect to each possible world.
Models: We use the term model in place of “possible world” when we need to be precise. Possible world might be thought of as (potentially) real environments that the agent might or might not be in, models are mathematical abstractions, each of which simply fixes the truth or falsehood of every relevant sentences.
If a sentence α is true in model m, we say that m satisfies α, or m is a model of α. Notation M(α) means the set of all models of α.
The relationship of entailment between sentence is crucial to our understanding of reasoning. A sentence α entails another sentence β if β is true in all world where α is true. Equivalent definitions include the validity of the sentence α⇒β and the unsatisfiability of sentence α∧¬β.
Logical entailment: The relation between a sentence and another sentence that follows from it.
Mathematical notation: α ⊨ β: αentails the sentence β.
Formal definition of entailment:
α ⊨ β if and only if M(α) ⊆ M(β)
i.e. α ⊨ β if and only if, in every model in which αis true, β is also true.
(Notice: if α ⊨ β, then α is a stronger assertion than β: it rules out more possible worlds. )
Logical inference: The definition of entailment can be applied to derive conclusions.
E.g. Apply analysis to the wupus-world.

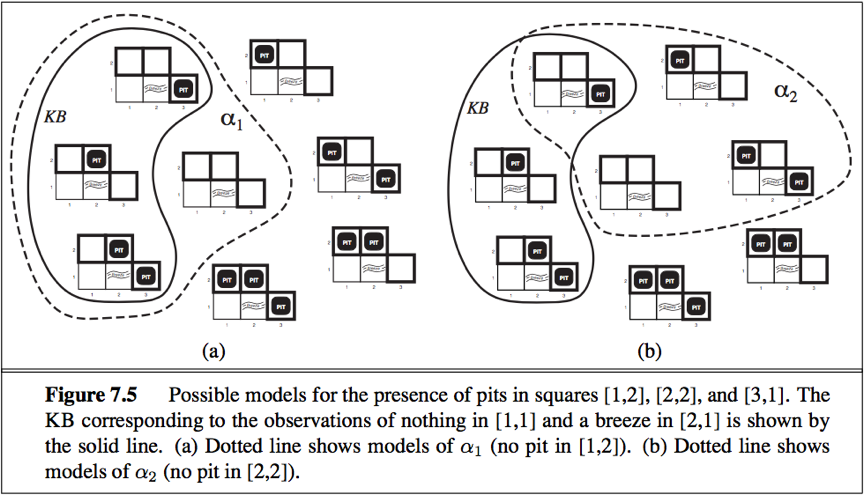
The KB is false in models that contradict what the agent knows. (e.g. The KB is false in any model in which [1,2] contains a pit because there is no breeze in [1, 1]).
Consider 2 possible conclusions α1and α2.
We see: in every model in which KB is true,α1 is also true. Hence KB⊨α1 , so the agent can conclude that there is no pit in [1, 2].
We see: in some models in which KB is true,α2 is false. Hence KB⊭α2, so the agent cannot conclude that there is no pit in [1, 2].
The inference algorithm used is called model checking: Enumerate all possible models to check that α is true in all models in which KB is true, i.e. M(KB) ⊆ M(α).
If an inference algorithm i can derive α from KB, we write KB⊨iα,pronounced as “α is derived from KB by i” or “i derives α from KB.”
Sound/truth preserving: An inference algorithm that derives only entailed sentences. Soundness is a highly desirable property. (e.g. model checking is a sound procedure when it is applicable.)
Completeness: An inference algorithm is complete if it can derive any sentence that is entailed. Completeness is also a desirable property.
Inference is the process of deriving new sentences from old ones. Sound inference algorithms derive only sentences that are entailed; complete algorithms derive all sentences that are entailed.
If KB is true in the real world, then any sentence α derived from KB by a sound inference procedure is also true in the real world.

Grounding: The connection between logical reasoning process and the real environment in which the agent exists.
In particular, how do we know that KB is true in the real world?
Propositional logic
Propositional logic is a simple language consisting of proposition symbols and logical connectives. It can handle propositions that are known true, known false, or completely unknown.
1. Syntax
The syntax defines the allowable sentences.
Atomic sentences: consist of a single proposition symbol, each such symbol stands for a proposition that can be true or false. (e.g. W1,3 stand for the proposition that the wumpus is in [1, 3].)
Complex sentences: constructed from simpler sentences, using parentheses and logical connectives.

Semantics
The semantics defines the rules for determining the truth of a sentence with respect to a particular model.
The semantics for propositional logic must specify how to compute the truth value of any sentence, given a model.
For atomic sentences: The truth value of every other proposition symbol must be specified directly in the model.
For complex sentences:

A simple inference procedure
To decide whether KB ⊨ α for some sentence α:
Algorithm 1: Model-checking approach
Enumerate the models (assignments of true or false to every relevant proposition symbol), check that α is true in every model in which KB is true.
e.g.

TT-ENTAILS?: A general algorithm for deciding entailment in propositional logic, performs a recursive enumeration of a finite space of assignments to symbols.
Sound and complete.
Time complexity: O(2n)
Space complexity: O(n), if KB and α contain n symbols in all.

Propositional theorem proving
We can determine entailment by model checking (enumerating models, introduced above) or theorem proving.
Theorem proving: Applying rules of inference directly to the sentences in our knowledge base to construct a proof of the desired sentence without consulting models.
Inference rules are patterns of sound inference that can be used to find proofs. The resolution rule yields a complete inference algorithm for knowledge bases that are expressed in conjunctive normal form. Forward chaining and backward chaining are very natural reasoning algorithms for knowledge bases in Horn form.
Logical equivalence:
Two sentences α and β are logically equivalent if they are true in the same set of models. (write as α ≡ β).
Also: α ≡ β if and only if α ⊨ β and β ⊨ α.

Validity: A sentence is valid if it is true in all models.
Valid sentences are also known as tautologies—they are necessarily true. Every valid sentence is logically equivalent to True.
The deduction theorem: For any sentence αand β, α ⊨ β if and only if the sentence (α ⇒ β) is valid.
Satisfiability: A sentence is satisfiable if it is true in, or satisfied by, some model. Satisfiability can be checked by enumerating the possible models until one is found that satisfies the sentence.
The SAT problem: The problem of determining the satisfiability of sentences in propositional logic.
Validity and satisfiability are connected:
α is valid iff ¬α is unsatisfiable;
α is satisfiable iff ¬α is not valid;
α ⊨ β if and only if the sentence (α∧¬β) is unsatisfiable.
Proving β from α by checking the unsatisfiability of (α∧¬β) corresponds to proof by refutation / proof by contradiction.
Inference and proofs
Inferences rules (such as Modus Ponens and And-Elimination) can be applied to derived to a proof.
·Modus Ponens:
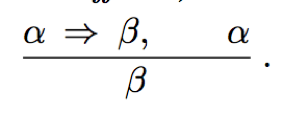
Whenever any sentences of the form α⇒β and α are given, then the sentence β can be inferred.
·And-Elimination:
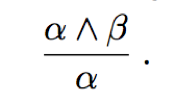
From a conjunction, any of the conjuncts can be inferred.
·All of logical equivalence (in Figure 7.11) can be used as inference rules.

e.g. The equivalence for biconditional elimination yields 2 inference rules:
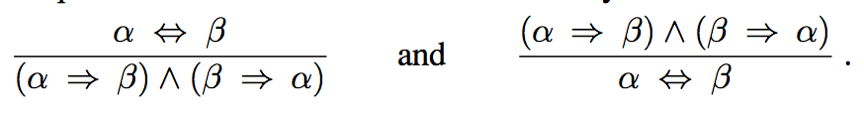
·De Morgan’s rule
We can apply any of the search algorithms in Chapter 3 to find a sequence of steps that constitutes a proof. We just need to define a proof problem as follows:
·INITIAL STATE: the initial knowledge base;
·ACTION: the set of actions consists of all the inference rules applied to all the sentences that match the top half of the inference rule.
·RESULT: the result of an action is to add the sentence in the bottom half of the inference rule.
·GOAL: the goal is a state that contains the sentence we are trying to prove.
In many practical cases, finding a proof can be more efficient than enumerating models, because the proof can ignore irrelevant propositions, no matter how many of them they are.
Monotonicity: A property of logical system, says that the set of entailed sentences can only increased as information is added to the knowledge base.
For any sentences α and β,
If KB ⊨ αthen KB ∧β ⊨ α.
Monotonicity means that inference rules can be applied whenever suitable premises are found in the knowledge base, what else in the knowledge base cannot invalidate any conclusion already inferred.
Proof by resolution
Resolution: An inference rule that yields a complete inference algorithm when coupled with any complete search algorithm.
Clause: A disjunction of literals. (e.g. A∨B). A single literal can be viewed as a unit clause (a disjunction of one literal ).
Unit resolution inference rule: Takes a clause and a literal and produces a new clause.
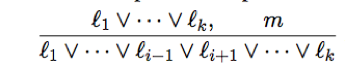
where each l is a literal, li and m are complementary literals (one is the negation of the other).
Full resolution rule: Takes 2 clauses and produces a new clause.
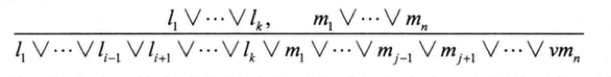
where li and mj are complementary literals.
Notice: The resulting clause should contain only one copy of each literal. The removal of multiple copies of literal is called factoring.
e.g. resolve(A∨B) with (A∨¬B), obtain(A∨A) and reduce it to just A.
The resolution rule is sound and complete.
Conjunctive normal form
Conjunctive normal form (CNF): A sentence expressed as a conjunction of clauses is said to be in CNF.
Every sentence of propositional logic is logically equivalent to a conjunction of clauses, after converting a sentence into CNF, it can be used as input to a resolution procedure.
A resolution algorithm

e.g.
KB = (B1,1⟺(P1,2∨P2,1))∧¬B1,1
α = ¬P1,2
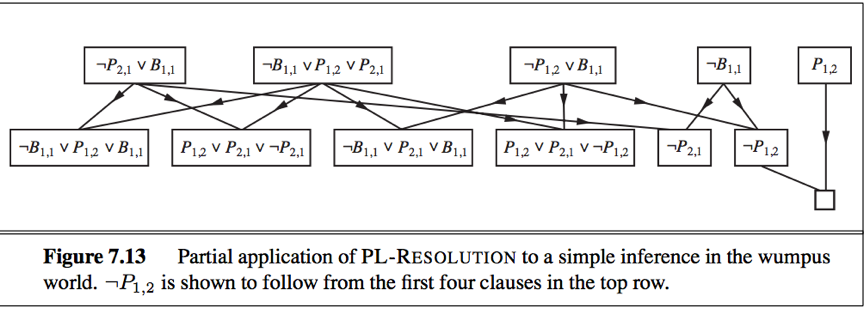
Notice: Any clause in which two complementary literals appear can be discarded, because it is always equivalent to True.
e.g. B1,1∨¬B1,1∨P1,2 = True∨P1,2 = True.
PL-RESOLUTION is complete.
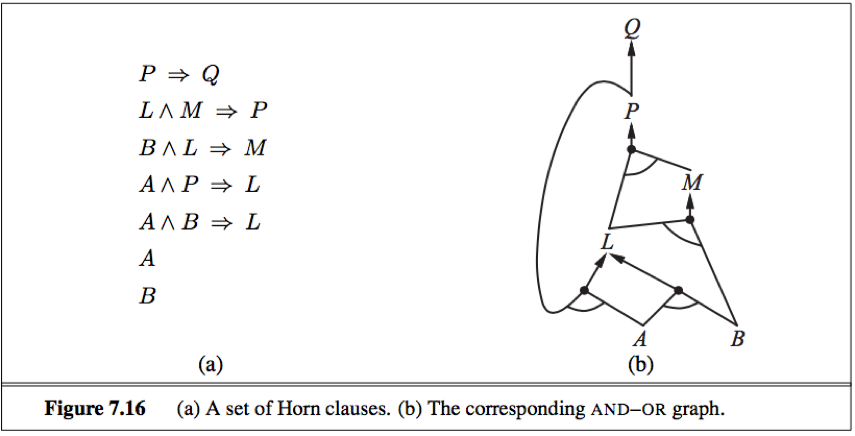
Horn clauses and definite clauses
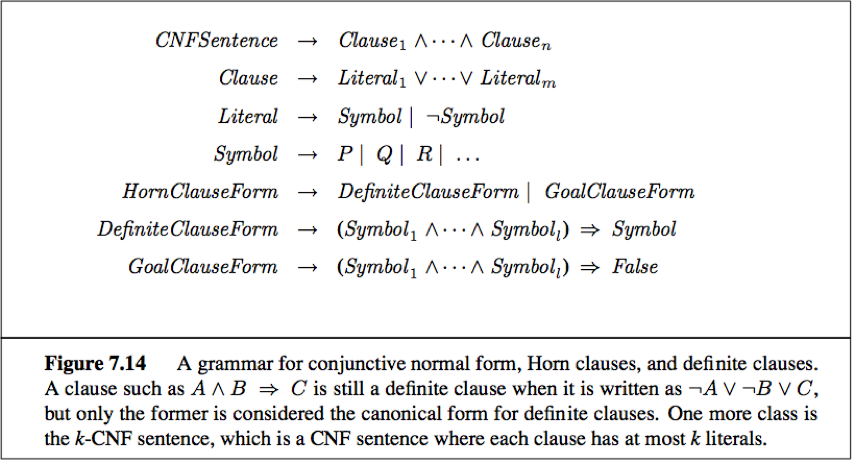
Definite clause: A disjunction of literals of which exactly one is positive. (e.g. ¬ L1,1∨¬Breeze∨B1,1)
Every definite clause can be written as an implication, whose premise is a conjunction of positive literals and whose conclusion is a single positive literal.
Horn clause: A disjunction of literals of which at most one is positive. (All definite clauses are Horn clauses.)
In Horn form, the premise is called the body and the conclusion is called the head.
A sentence consisting of a single positive literal is called a fact, it too can be written in implication form.
Horn clause are closed under resolution: if you resolve 2 horn clauses, you get back a horn clause.
Inference with horn clauses can be done through the forward-chaining and backward-chaining algorithms.
Deciding entailment with Horn clauses can be done in time that is linear in the size of the knowledge base.
Goal clause: A clause with no positive literals.
Forward and backward chaining
forward-chaining algorithm: PL-FC-ENTAILS?(KB, q) (runs in linear time)
Forward chaining is sound and complete.

e.g. A knowledge base of horn clauses with A and B as known facts.
fixed point: The algorithm reaches a fixed point where no new inferences are possible.
Data-driven reasoning: Reasoning in which the focus of attention starts with the known data. It can be used within an agent to derive conclusions from incoming percept, often without a specific query in mind. (forward chaining is an example)
Backward-chaining algorithm: works backward rom the query.
If the query q is known to be true, no work is needed;
Otherwise the algorithm finds those implications in the KB whose conclusion is q. If all the premises of one of those implications can be proved true (by backward chaining), then q is true. (runs in linear time)
in the corresponding AND-OR graph: it works back down the graph until it reaches a set of known facts.
(Backward-chaining algorithm is essentially identical to the AND-OR-GRAPH-SEARCH algorithm.)
Backward-chaining is a form of goal-directed reasoning.
Effective propositional model checking
The set of possible models, given a fixed propositional vocabulary, is finite, so entailment can be checked by enumerating models. Efficient model-checking inference algorithms for propositional logic include backtracking and local search methods and can often solve large problems quickly.
2 families of algorithms for the SAT problem based on model checking:
a. based on backtracking
b. based on local hill-climbing search
1. A complete backtracking algorithm
David-Putnam algorithm (DPLL):

DPLL embodies 3 improvements over the scheme of TT-ENTAILS?: Early termination, pure symbol heuristic, unit clause heuristic.
Tricks that enable SAT solvers to scale up to large problems: Component analysis, variable and value ordering, intelligent backtracking, random restarts, clever indexing.
Local search algorithms
Local search algorithms can be applied directly to the SAT problem, provided that choose the right evaluation function. (We can choose an evaluation function that counts the number of unsatisfied clauses.)
These algorithms take steps in the space of complete assignments, flipping the truth value of one symbol at a time.
The space usually contains many local minima, to escape from which various forms of randomness are required.
Local search methods such as WALKSAT can be used to find solutions. Such algorithm are sound but not complete.
WALKSAT: one of the simplest and most effective algorithms.

On every iteration, the algorithm picks an unsatisfied clause, and chooses randomly between 2 ways to pick a symbol to flip:
Either a. a “min-conflicts” step that minimizes the number of unsatisfied clauses in the new state;
Or b. a “random walk” step that picks the symbol randomly.
When the algorithm returns a model, the input sentence is indeed satifiable;
When the algorithm returns failure, there are 2 possible causes:
Either a. The sentence is unsatisfiable;
Or b. We need to give the algorithm more time.
If we set max_flips=∞, p>0, the algorithm will:
Either a. eventually return a model if one exists
Or b. never terminate if the sentence is unsatifiable.
Thus WALKSAT is useful when we expect a solution to exist, but cannot always detect unsatisfiability.
The landscape of random SAT problems
Underconstrained problem: When we look at satisfiability problems in CNF, an underconstrained problem is one with relatively few clauses constraining the variables.
An overconstrained problem has many clauses relative to the number of variables and is likely to have no solutions.
The notation CNFk(m, n) denotes a k-CNF sentence with m clauses and n symbols. (with n variables and k literals per clause).
Given a source of random sentences, where the clauses are chosen uniformly, independently and without replacement from among all clauses with k different literals, which are positive or negative at random.
Hardness: problems right at the threshold > overconstrained problems > underconstrained problems
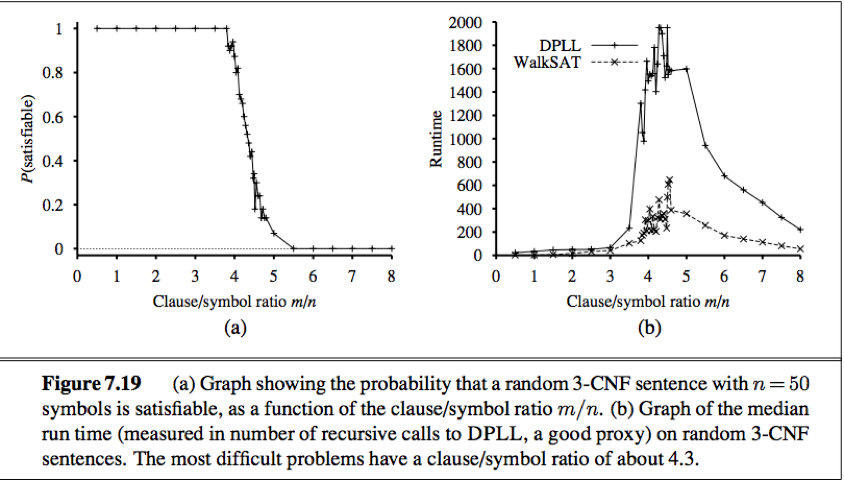
Satifiability threshold conjecture: A theory says that for every k≥3, there is a threshold ratio rk, such that as n goes to infinity, the probability that CNFk(n, rn) is satisfiable becomes 1 for all values or r below the threshold, and 0 for all values above. (remains unproven)
Agent based on propositional logic
1. The current state of the world
We can associate proposition with timestamp to avoid contradiction.
e.g. ¬Stench3, Stench4
fluent: refer an aspect of the world that changes. (E.g. Ltx,y)
atemporal variables: Symbols associated with permanent aspects of the world do not need a time superscript.
Effect axioms: specify the outcome of an action at the next time step.
Frame problem: some information lost because the effect axioms fails to state what remains unchanged as the result of an action.
Solution: add frame axioms explicity asserting all the propositions that remain the same.
Representation frame problem: The proliferation of frame axioms is inefficient, the set of frame axioms will be O(mn) in a world with m different actions and n fluents.
Solution: because the world exhibits locaility (for humans each action typically changes no more than some number k of those fluents.) Define the transition model with a set of axioms of size O(mk) rather than size O(mn).
Inferential frame problem: The problem of projecting forward the results of a t step lan of action in time O(kt) rather than O(nt).
Solution: change one’s focus from writing axioms about actions to writing axioms about fluents.
For each fluent F, we will have an axiom that defines the truth value of Ft+1 in terms of fluents at time t and the action that may have occurred at time t.
The truth value of Ft+1 can be set in one of 2 ways:
Either a. The action at time t cause F to be true at t+1
Or b. F was already true at time t and the action at time t does not cause it to be false.
An axiom of this form is called a successor-state axiom and has this schema:
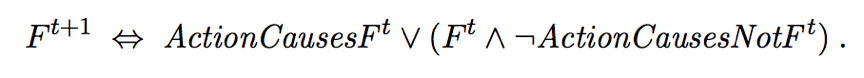
Qualification problem: specifying all unusual exceptions that could cause the action to fail.
2. A hybrid agent
Hybrid agent: combines the ability to deduce various aspect of the state of the world with condition-action rules, and with problem-solving algorithms.
The agent maintains and update KB as a current plan.
The initial KB contains the atemporal axioms. (don’t depend on t)
At each time step, the new percept sentence is added along with all the axioms that depend on t (such as the successor-state axioms).
Then the agent use logical inference by ASKING questions of the KB (to work out which squares are safe and which have yet to be visited).
The main body of the agent program constructs a plan based on a decreasing priority of goals:
1. If there is a glitter, construct a plan to grab the gold, follow a route back to the initial location and climb out of the cave;
2. Otherwise if there is no current plan, plan a route (with A* search) to the closest safe square unvisited yet, making sure the route goes through only safe squares;
3. If there are no safe squares to explore, if still has an arrow, try to make a safe square by shooting at one of the possible wumpus locations.
4. If this fails, look for a square to explore that is not provably unsafe.
5. If there is no such square, the mission is impossible, then retreat to the initial location and climb out of the cave.

Weakness: The computational expense goes up as time goes by.
3. Logical state estimation
To get a constant update time, we need to cache the result of inference.
Belief state: Some representation of the set of all possible current state of the world. (used to replace the past history of percepts and all their ramifications)
e.g. 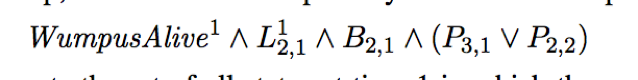
We use a logical sentence involving the proposition symbols associated with the current time step and the temporal symbols.
Logical state estimation involves maintaining a logical sentence that describes the set of possible states consistent with the observation history. Each update step requires inference using the transition model of the environment, which is built from successor-state axioms that specify how each fluent changes.
State estimation: The process of updating the belief state as new percepts arrive.
Exact state estimation may require logical formulas whose size is exponential in the number of symbols.
One common scheme for approximate state estimation: to represent belief state as conjunctions of literals (1-CNF formulas).
The agent simply tries to prove Xt and ¬Xt for each symbol Xt, given the belief state at t-1.
The conjunction of provable literals becomes the new belief state, and the previous belief state is discarded.
(This scheme may lose some information as time goes along.)
The set of possible states represented by the 1-CNF belief state includes all states that are in fact possible given the full percept history. The 1-CNF belief state acts as a simple outer envelope, or conservative approximation.

4. Making plans by propositional inference
We can make plans by logical inference instead of A* search in Figure 7.20.
Basic idea:
1. Construct a sentence that includes:
a) Init0: a collection of assertions about the initial state;
b) Transition1, …, Transitiont: The successor-state axioms for all possible actions at each time up to some maximum time t;
c) HaveGoldt∧ClimbedOutt: The assertion that the goal is achieved at time t.
2. Present the whole sentence to a SAT solver. If the solver finds a satisfying model, the goal is achievable; else the planning is impossible.
3. Assuming a model is found, extract from the model those variables that represent actions and are assigned true.
Together they represent a plan to ahieve the goals.
Decisions within a logical agent can be made by SAT solving: finding possible models specifying future action sequences that reach the goal. This approach works only for fully observable or sensorless environment.
SATPLAN: A propositional planning. (Cannot be used in a partially observable environment)
SATPLAN finds models for a sentence containing the initial sate, the goal, the successor-state axioms, and the action exclusion axioms.
(Because the agent does not know how many steps it will take to reach the goal, the algorithm tries each possible number of steps t up to some maximum conceivable plan length Tmax.)

Precondition axioms: stating that an action occurrence requires the preconditions to be satisfied, added to avoid generating plans with illegal actions.
Action exclusion axioms: added to avoid the creation of plans with multiple simultaneous actions that interfere with each other.
Propositional logic does not scale to environments of unbounded size because it lacks the expressive power to deal concisely with time, space and universal patterns of relationshipgs among objects.



