Find the longest route with the smallest starting point

前提：对于一个给定的二维整数矩阵，如果一个元素i的某个4-相邻位置上的另一个元素j正好值为i-1则i到j可以形成一条通路。

输入：M个N*N整数矩阵；

输出：对于每个输入的矩阵，输出 矩阵中可形成的最长通路长度 及 在该最长通路长度的情况下最小的起始点值。

 e.g.

input:

4 5 6 1 2 3 7 0 5 8 2 1 6 7 3 4

 

 

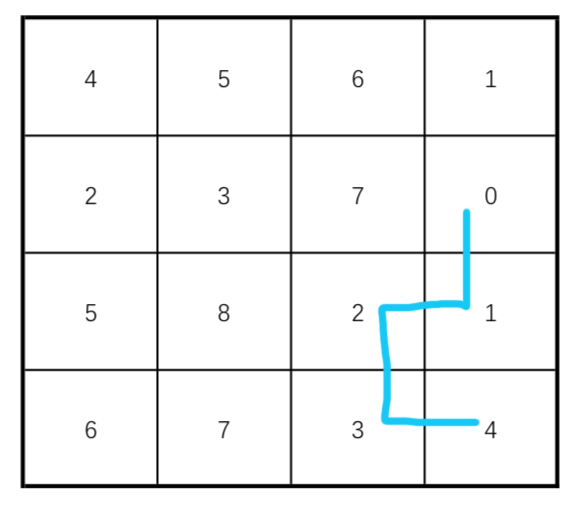
output:

4 0

 

idea:

遍历输入矩阵中每个位置，compute()计算以该位置为起点的最长route长度->找出 最长route长度 及 该长度下最小的起点值。

compute(r,c)

 

traverse 4个方向上的相邻位置：
       if 当前位置到该相邻位置(nr,nc)可以形成通路（input[r][c]==input[nr][nc]-1)
             neighbor_route_length:=compute(nr,nc)
       end    
end
 if traverse 完4个方向上都没形成任何通路，返回0    
 else 有找到通路，返回 neighbor_route_length的最大值+1

 

 

-----------------------------------分割线

 

可以引入缓存矩阵buffer[N][N]作为hash table存储先前计算过的compute(r,c)值

i.e. 对于某个确定可以形成通路的相邻位置(nr,nc)，如果buffer中有缓存已经计算过的route_length值，则不再调用compute，直接提取buffer[nr][nc]。

compute2(r,c)

traverse 4个方向上的相邻位置：
       if 当前位置到该相邻位置(nr,nc)可以形成通路（input[r][c]==input[nr][nc]-1)
            if  buffer[nr][nc]已有记录
                neighbor_route_length:=buffer[nr][nc]
            else //没有记录
                neighbor_route_length:=compute(nr,nc)
            end
       end    
end
 if traverse 完4个方向上都没形成任何通路，返回0    
 else 有找到通路，返回 neighbor_route_length的最大值+1

 

 

code：

class Solution {
  public:
    pair<int,int> getAnswer(vector<vector<int>> input) {
        int N=input.size();
        vector<vector<int>> buffer(N,vector<int>(N,-1));
        int longest_length=-1, starting_point=-1;
        for (int r=0;r<N;r++) {
            for (int c=0;c<N;c++) {
                int current_length=compute_route(N,input,buffer,r,c);
                if (current_length>longest_length||
                    (current_length==longest_length&&starting_point>input[r][c])) {
                    longest_length=current_length;
                    starting_point=input[r][c];
                }
            }
        }
        return pair<int,int>(longest_length, starting_point);
    }
    //虽然突然想起好像原始题目是每个位置的所有4个方向中只有最多一条通路
    //但是因为比较无聊就加大一点难度：每个位置有可能有多条通路 要找出最长的一条 罢了
    //what if there might be more than 1 route from a starting point
    int compute_route(int N, vector<vector<int>>& input, vector<vector<int>>& buffer, int r, int c) {
        int neighbors[4][2]={{r-1,c},{r,c-1},{r,c+1},{r+1,c}};
        int neighbor_route_length=-1, answer;
        for (int i=0;i<4;i++) {
            int neighbor_r=neighbors[i][0], neighbor_c=neighbors[i][1];
            if (neighbor_r>=0&&neighbor_r<N&&neighbor_c>=0&&neighbor_c<N) {
                if (input[neighbor_r][neighbor_c]==input[r][c]+1) {
                    if (buffer[neighbor_r][neighbor_c]!=-1) {
                        neighbor_route_length=max(neighbor_route_length, buffer[neighbor_r][neighbor_c]);
                    } else {
                        neighbor_route_length=max(neighbor_route_length,compute_route(N, input, buffer, neighbor_r, neighbor_c));
                    }
                }
            }
        }
        if (neighbor_route_length==-1) //no route found
            answer=0;
        else
            answer=neighbor_route_length+1;
        buffer[r][c]=answer;
        return answer;
    }
};