2022面向对象设计与构造第一单元总结

一、程序结构度量

1.1 第一次作业

1.1.1 类的度量

各类的规模

类	属性个数	方法个数	类代码规模
Task1(主类)	0	4	151行
Polynomial	3	2	52行
Term	1	5	123行
BasePoly	3	2	89行
BaseTerm	2	6	64行

各方法的规模（采用IDEA MetricReloaded 插件，下同）

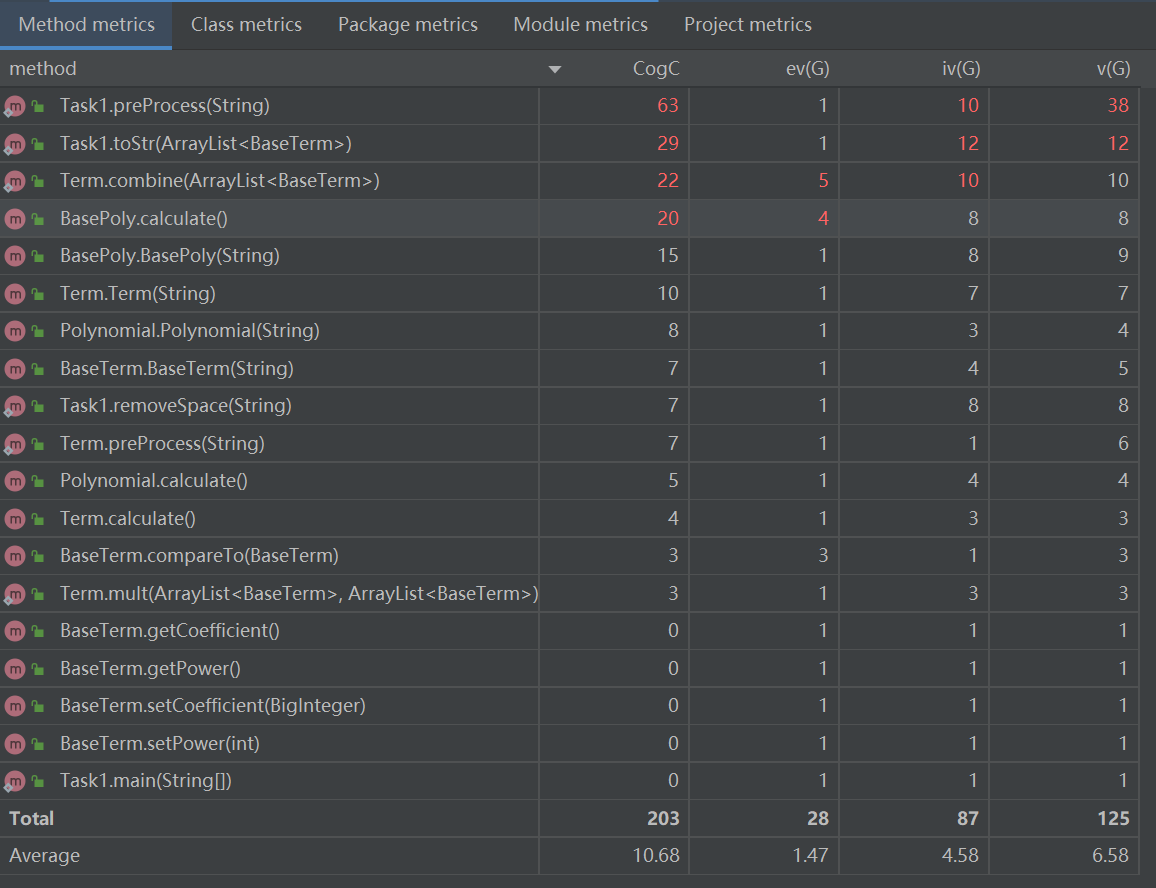
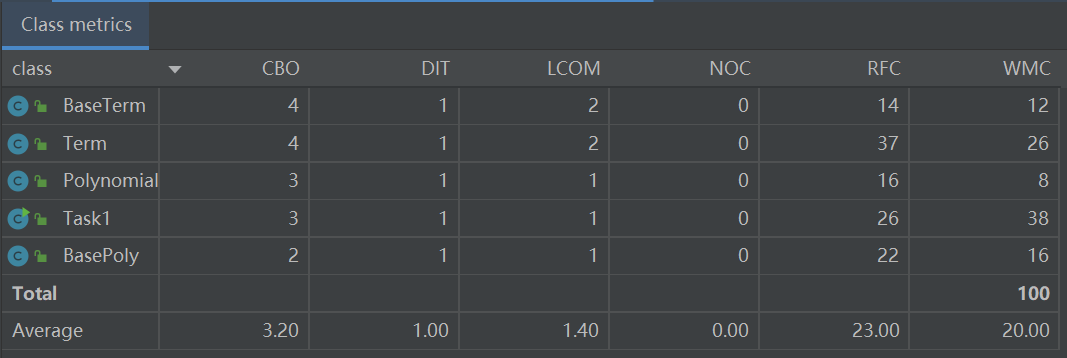
类的内聚耦合（CBO：耦合度，LCOM：内聚缺失度，下同）

由于在完成第一次作业时，我没有认真阅读指导书，误以为测试数据会出现不符合格式的情况，所以在代码中加入了很多格式判断语句，大大增加了总代码规模和一些方法的规模。例如主类中151行代码，至少有一般代码是在进行格式判断。

由类的内聚耦合表可见，各类的CBO值和LCOM值均较低，符合高内聚第耦合的设计要求。

1.1.2 UML图

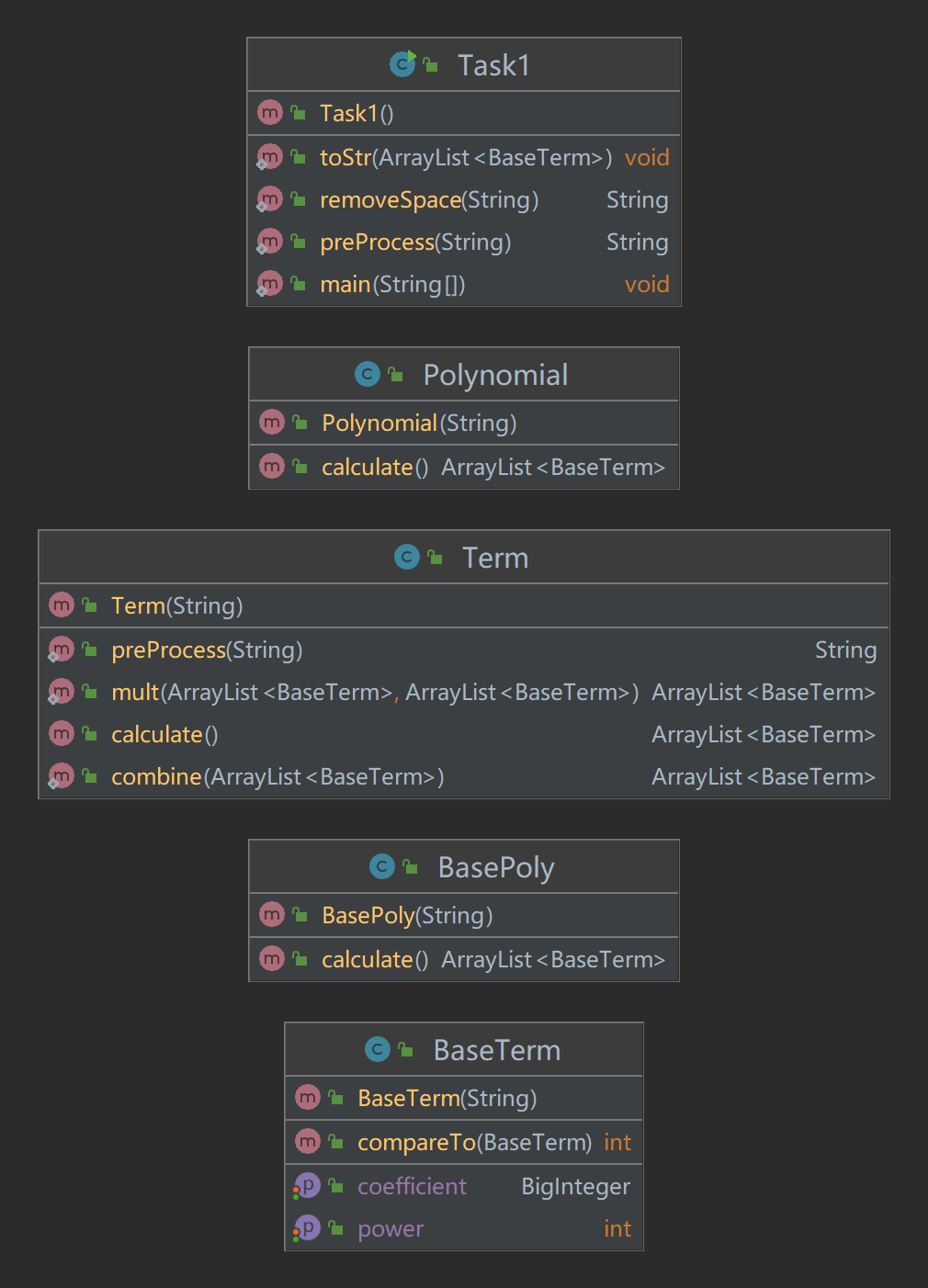
设计考虑

• 我的第一次作业一共使用了5个类，其中主类主要是用来进行预处理以及输出，各类之间均没有继承关系。因为第一次作业最多只有一层括号，所以我设计了Polynamial，Term，BasePoly，BaseTerm四个类，分别表示（最多）带一层括号的表达式、（最多）带一层括号的项、不带括号的表达式、不带括号的项。通过这四个类，将原始表达式一步步向下拆分传递，直至获得a*x**b形式的“基项”。
• 鉴于项与项之间的关系有加减两种可能，不适合使用容器存储在表达式类中，所以我为表达式类设计了三个属性：项类、操作符以及子表达式类。这样利用二叉树的架构将项类存储于表达式类。
• 为了实现化简后表达式的导出，我为这四个类都实现了一种calculate()方法，上层类得到下层类的化简结果之后进行进一步化简，类与类之间使用基项容器传递化简结果。
• 事实上，为了输出的美观，我还为基项类实现了Comparable接口，以实现输出时各项的有序。虽然在这次作业中它没有发挥实际的作用，但到了第三次作业，它就为项与项之间的相等判断提供了很大的便利。

优缺点

优点

• 设计功能明确，易于理解。

缺点

• 各类抽象化程度不高，架构不利于扩展，虽然后续两次作业我也没有重构，但确实体会到了对于扩展的不利影响。
• 类的分工不够明确，比如主类中本不该出现的输出方法。
• 个别方法逻辑过于复杂，可读性不强。
• 长度优化不足，没有将正项调整到第一项。

1.2 第二次作业

1.2.1 类的度量

各类的规模

类	属性个数	方法个数	类代码规模
Task2(主类)	0	1	20行
Polynomial	3	2	52行
Term	1	5	143行
BasePoly	3	2	91行
BaseTerm	4	8	234行
TrigoFunction	3	4	103行
Function	3	2	57行
Operation	0	15	426行

各方法的规模（部分）

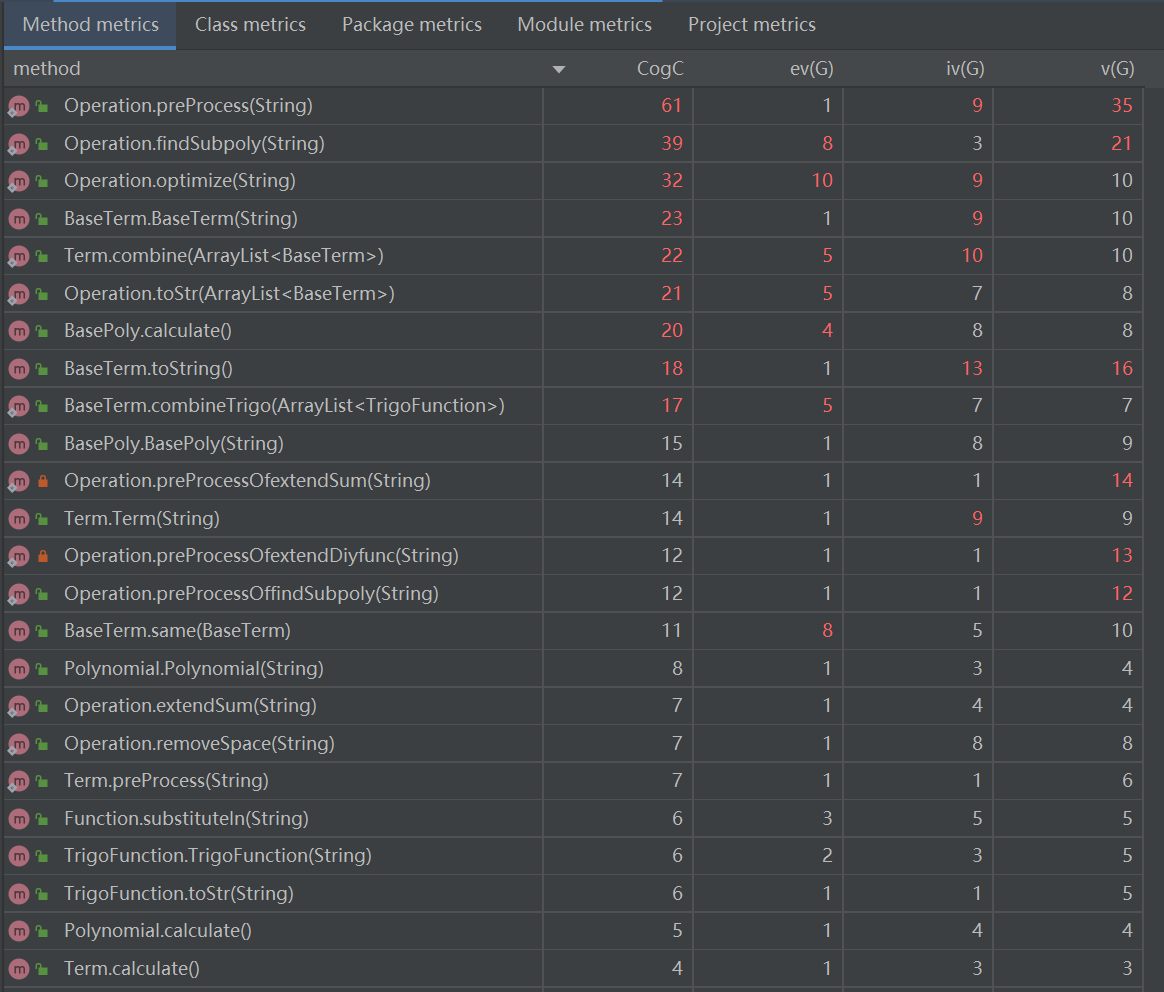
类的内聚耦合

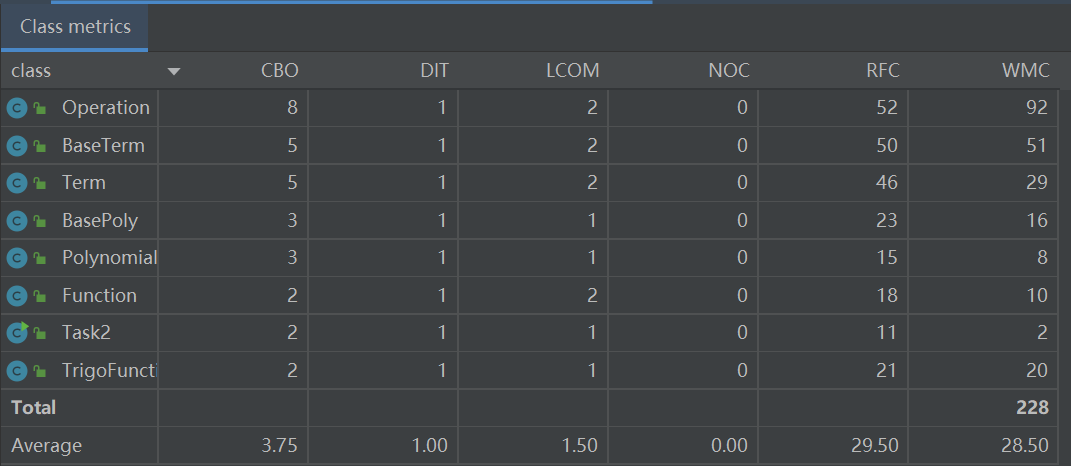
第二次作业的需求相对于第一次作业复杂了许多，因此肉眼可见地导致代码总规模和各类的规模都有不少的增长。但因为我在第二次作业中更加注重类和方法的分工，例如将预处理方法和输出方法这些静态方法统一设置一个Operation类管理，这次代码的整体方法复杂度和类复杂度都有了明显的下降。不过受限于架构缺陷，仍然有不少复杂度飘红。

至于类的内聚耦合情况，通过表格可以发现，各类的LCOM值仍然普遍很低，高内聚情况很好。同时各类的CBO值也较低，总体符合高内聚低耦合的设计要求，仅有Operation这一个类的耦合度偏高，但仍在正常范围内。这主要是因为Operation类集成了很多静态方法，被大多数类所调用。由此可见，在正式工程中，还是把静态方法放在被需要的类中更加合理。

1.2.2 UML图

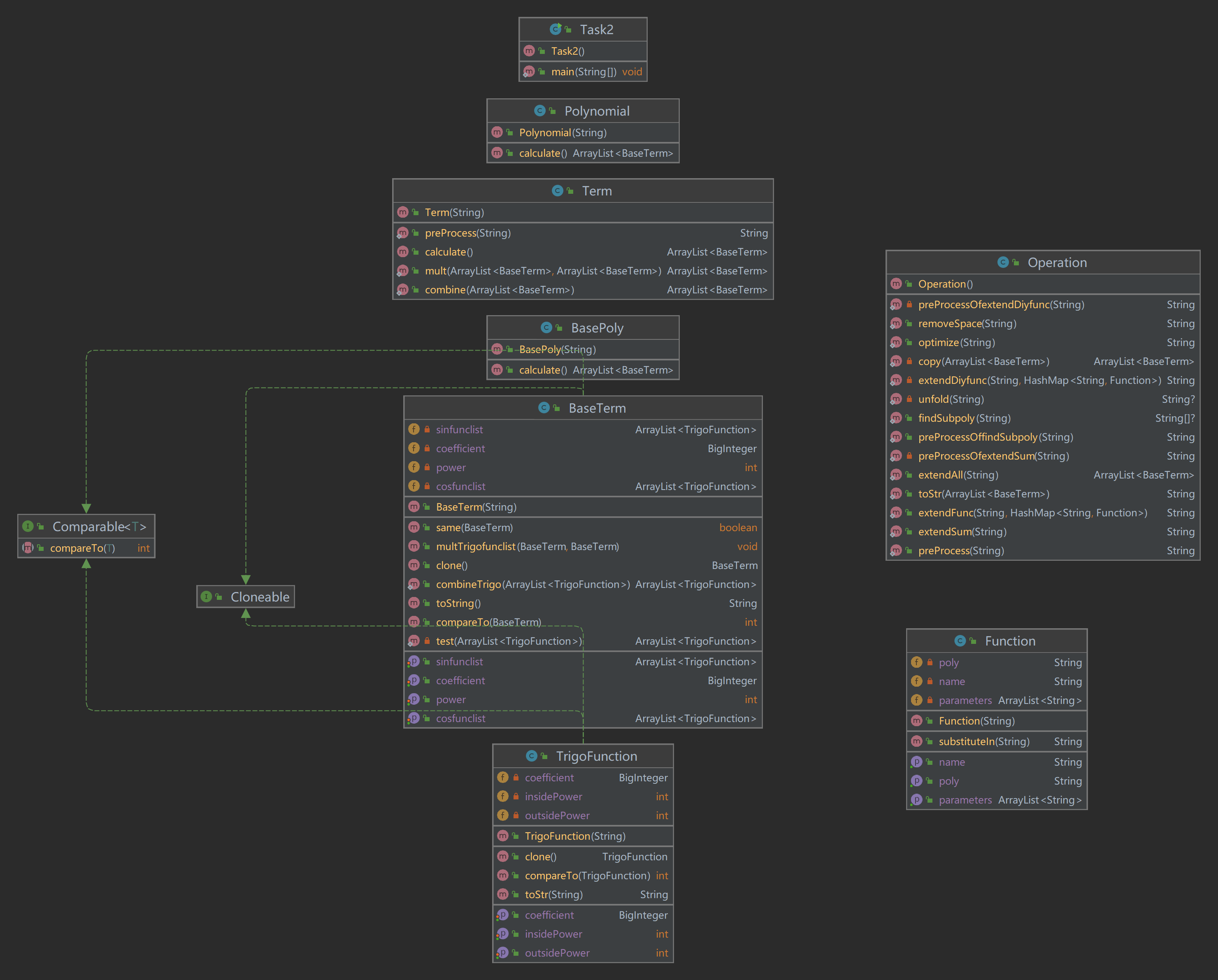
设计考虑

• 相对于第一次作业，我在本次作业中新增了TrigoFunction、Function、Operation三个类。类之间仍无继承关系。新增的三个类中，TrigoFunction类用于解析与存储基项类内部的三角函数，层次位于BaseTerm之下；Function类用来解析和存储输入的自定义函数；Operation类集成了一些预处理和长度优化的静态方法。
• 将静态方法集成到Operation类中，一方面是为了更加方便地管理，另一方面也提高了代码的高内聚低耦合度。
• 自定义函数代入时，首先进行x形参的代入，以避免错误扩大代入范围的bug。
• 为了实现多层嵌套括号的解析，我用了一种算是偷懒的办法：寻找表达式中的倒数第二内层括号，将括号中的内容进行解析（此时解析的必然只有一层括号，按第一次作业方法解析即可），返回化简表达式并进行字符串替换。循环进行上述操作直至去除所有非必要括号。
• 一些方法需要对TrigoFunction类和BaseTerm类进行深拷贝，故我让这两个类都实现了Cloneable接口并重写了Clone()方法。
• 实现了sin(x)**2+cos(x)**2=1、cos(0)=1、cos(-x)=cos(x)这些类型的输出长度优化。

优缺点

优点

• 逻辑易于理解，实现较为简单。
• 长度优化非常充分，在强测中各个测试点的性能分都拿到了满分。

缺点

• 对于函数代入，我的设计并未对自定义函数和求和函数进行建模，而是直接字符串代入，考虑不全面的话容易出现意想不到的bug。
• 类的高内聚低耦合程度仍然不够高，一些方法的逻辑比较复杂（比如长度优化方法，几经修改才把它限制在了60行以下）。
• 嵌套括号的处理采用循环处理而非递归处理，每次循环都需要对表达式进行一系列复杂的预处理，比较浪费时间。
• 和之前一样，类的抽象化程度还是不够高，十分不利于扩展。

1.3 第三次作业

1.3.1 类的度量

各类的规模

类	属性个数	方法个数	类代码规模
Task3(主类)	0	1	20行
Polynomial	3	2	52行
Term	1	5	146行
BasePoly	3	2	92行
BaseTerm	4	7	298行
TrigoFunction	2	7	114行
Function	3	2	57行
Operation	0	17	497行

各方法的规模（部分）

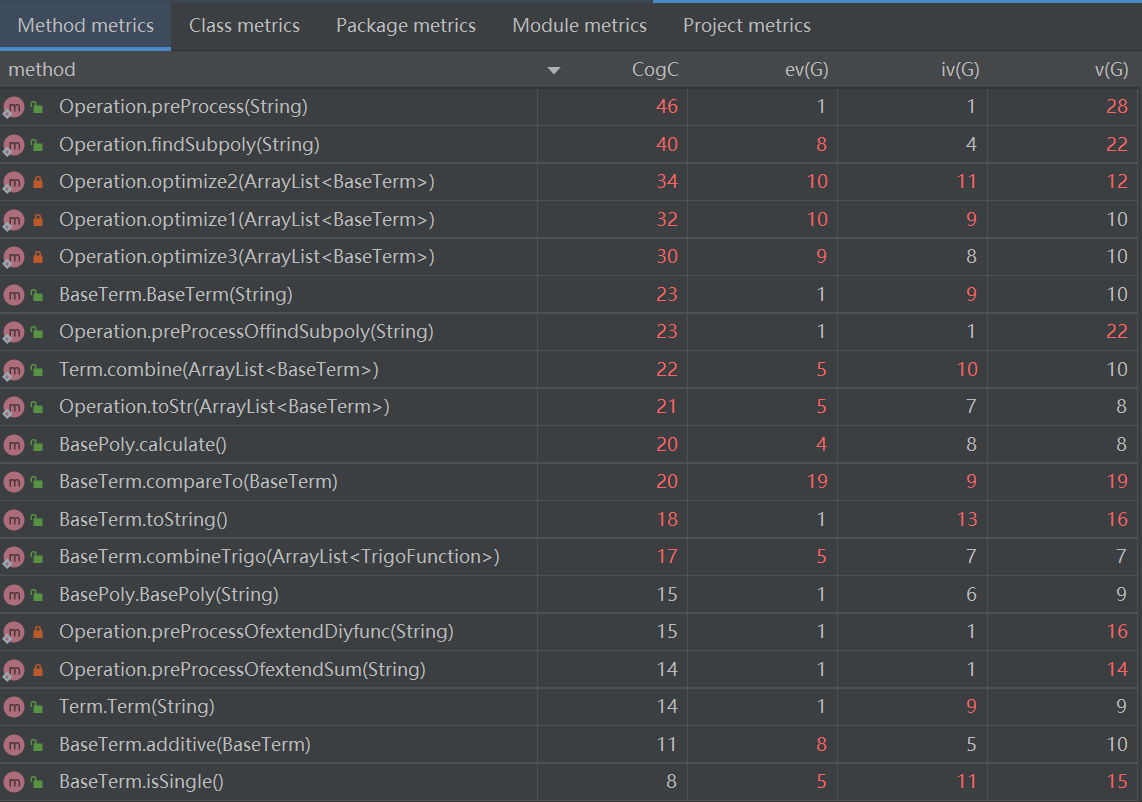
类的内聚耦合

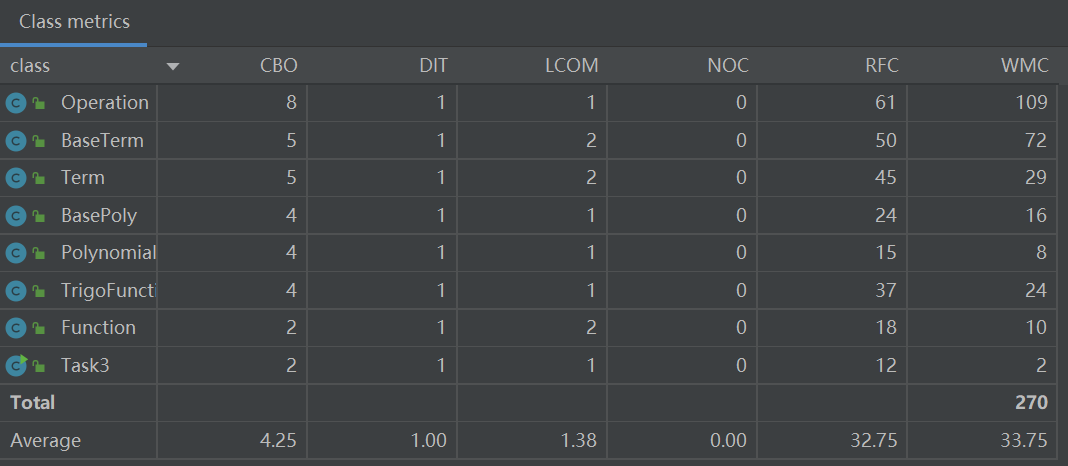
相比第二次作业，这次作业的方法复杂度整体上高了不少，这主要是因为主体架构不变但细节更加复杂，许多方法使用了较为复杂的逻辑。同时，因为确定这个单元的作业不会出现非法输入，所以我将代码中原本的格式判断语句全部删除。可以看到，Operation.preProcess方法的认知复杂度从63降到了46，方法得到了很大程度的简化。

第三次作业的内聚耦合情况与第二次作业大体相同，故不作额外分析。代码仍然符合高内聚低耦合的设计要求。

1.3.2 UML图

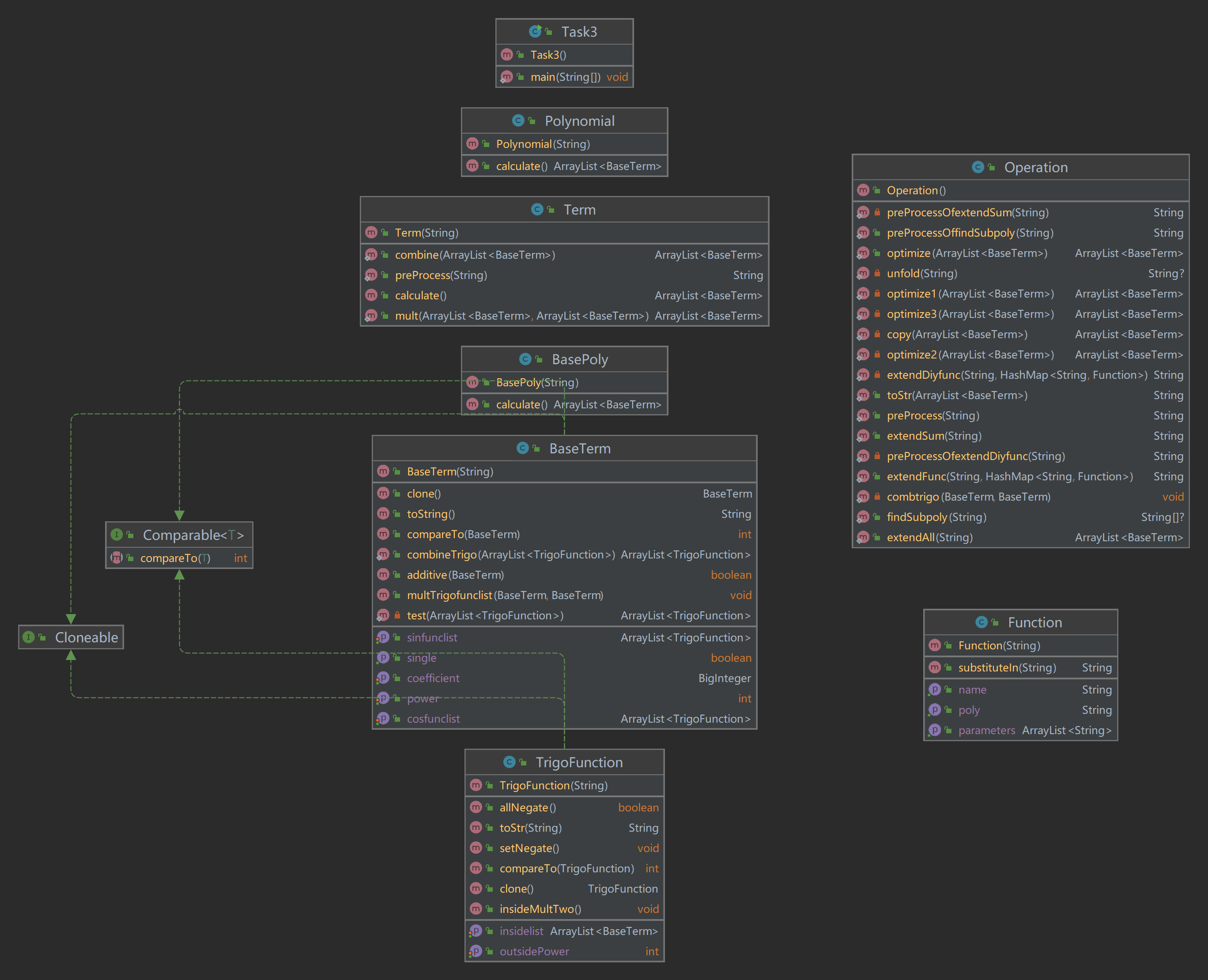
设计考虑

• 本次作业相比于上次并无类的增加。主要的改动有以下两个方面：
  1. 由于此次作业三角函数可以内嵌表达式，故将TrigoFunction的coefficient和insidePower属性删去，改为inside属性，数据类型为ArrayList<BaseTerm>。
  2. 由于此次作业可以有自定义函数的嵌套调用，所以我把预处理时对自定义函数的展开改为了循环，由外而内展开直至自定义函数被完全替换。
• 实现了cos(x)**2-sin(x)**2=cos((2*x))， 2*sin(x)*cos(x)=sin((2*x))这些类的长度优化。

优缺点

优点

• 和之前的优点类似。

缺点

• 直接进行表达式字符串替换，容易产生bug。
• 长度优化不够彻底，比如cos(x)**4-sin(x)**4=cos((2*x))这样的化简方式没有考虑到。

二、BUG分析

2.1 自己的bug

2.1.1 第一次作业

初测

很不幸的是，第一次作业的初测就错了两个测试点，而且对应两个不同的bug：

1. 低估了常数的范围，误以为只会出现int类型的常数，后来改为了BigInteger后通过。
2. Term类中的一个逻辑错误：

    public ArrayList<BaseTerm> calculate() {
        ArrayList<BaseTerm> result = new ArrayList<>();
        for (BasePoly basePoly : this.basePolyArrayList) {
            if (result.size() == 0) {
                result = basePoly.calculate();
            }
            else {
                result = mult(result, basePoly.calculate());
            }
        }
        result = combine(result);
        return result;
    }

如果出现类似于0*x*1这样的输入，那么第一次循环返回空ArrayList，第二次循环就会直接错误地以1作为循环结果。后改进了逻辑得以通过。

该方法的代码行数和圈复杂度与其他方法相比均处于中下水平。

强测和互测

均无bug

2.1.2 第二次作业

2.1.3 第三次作业

均无bug

2.2 寻找别人的bug

• 测试策略：暴力测试。
• 数据生成方法：根据形式化描述递归生成测试数据。
• 对拍方法：基于python sympy库进行对拍。
• 代码（以第三次为例）：

1.数据生成代码（有借鉴讨论区）：

点击查看代码

import random
import sys

sys.setrecursionlimit(1000000)  # 例如这里设置为一百万
OP = ['', '+', '-']
TRIGO = ["sin", "cos"]
NUM_MAX_LEN = 8            # 常数最大长度
TERM_MAX_SCALE = 3          # 一个项最多含有多少个因子
EXPR_MAX_SCALE = 3          # 一个表达式最多含有多少个项
SUB_EXPR_MAX_SCALE = 3      # 一个括号里的表达式最多含有多少个项
BRACKET_MAX_LEN = 3         # 括号嵌套层数
TRIGO_BRACKET_LEN = 3       # 三角函数嵌套层数


# 指数
def new_power():
    power_str = ""
    if random.randint(0, 1) > 0:
        power_str += "**"
        power_str += OP[random.randint(0, 1)]
        power_str += str(random.randint(0, 4))
    # print(power_str)
    return power_str


# 常数因子
def new_num():
    while 1:
        num_str = ""

        num_str += OP[random.randint(0, 2)]
        type = random.randint(0,5)
        if type == 0:
            return num_str + "0"
        elif type > 0 and type <=4:
            num_len = random.randint(1, NUM_MAX_LEN//3)
        else:
            num_len = random.randint(NUM_MAX_LEN//2, NUM_MAX_LEN)

        for i in range(num_len):
            num_str += str(random.randint(0, 9))
        if len(num_str) > 1 and num_str[0]!='0' and num_str[1]!='0':
            break
        if len(num_str) <= 1:
            break
        if len(num_str)==2 and num_str[1]=='0':
            break
    # print(num_str)
    return num_str


# 幂函数
def new_var():
    var_str = "x"

    var_str += new_power()

    # print(var_str)
    return var_str

def new_powerFunct(trigo_cnt):
    if trigo_cnt == 0:
        type = random.randint(1, 3)
    else:
        type = random.randint(0, 3)
    if type == 0 :
        return new_trigo(trigo_cnt - 1)
    elif type == 1:
        return new_var()
    elif type == 2:
        return new_num()
    else:
        return "(" + new_expr(random.randint(1, EXPR_MAX_SCALE), random.randint(0, BRACKET_MAX_LEN)) + ")" +new_power()


def new_trigo(trigo_cnt):
    str_trigo = TRIGO[random.randint(0,1)]
    str_trigo += "("
    str_trigo += new_powerFunct(trigo_cnt);
    str_trigo += ")"
    str_trigo += new_power();
    return str_trigo

# 因子
def new_factor(bracket_cnt, trigo_cnt):
    if bracket_cnt == 0:
        factor_type = random.randint(1, 3)
    else:
        factor_type = random.randint(0, 3)

    if factor_type == 0:
        return "(" + new_expr(random.randint(1, SUB_EXPR_MAX_SCALE), bracket_cnt - 1) + ")" + new_power()
    elif factor_type == 1:
        return new_num()
    elif factor_type == 2:
        return new_var()
    else:
        return new_trigo(trigo_cnt - 1)


# 项
def new_term(factor_cnt=1, bracket_cnt=1, trigo_cnt = 1):
    term_str = ""

    if factor_cnt == 1:
        term_str += OP[random.randint(0, 2)]
        term_str += new_factor(bracket_cnt, trigo_cnt)
    else:
        factor_cnt -= 1
        term_str += new_term(factor_cnt, bracket_cnt, trigo_cnt)
        term_str += "*"
        term_str += new_factor(bracket_cnt, trigo_cnt)

    # print(term_str)
    return term_str


# 表达式
def new_expr(term_cnt=1, bracket_cnt=1, trigo_cnt=1):
    expr_str = ""

    if term_cnt == 1:
        expr_str += OP[random.randint(0, 2)]
    else:
        term_cnt -= 1
        expr_str += new_expr(term_cnt, bracket_cnt,trigo_cnt)
        expr_str += OP[random.randint(1, 2)]

    expr_str += new_term(random.randint(1, TERM_MAX_SCALE), bracket_cnt, trigo_cnt)

    # print(expr_str)
    return expr_str

f=open('C:/Users/Dell/Desktop/sj.txt','w')
lst=[]
if __name__ == "__main__":
    for i in range(5000):
        while 1:
            expr = new_expr(random.randint(1, EXPR_MAX_SCALE), random.randint(0, BRACKET_MAX_LEN), random.randint(1, TRIGO_BRACKET_LEN))
            if len(expr) <= 100:
                break
        expr=expr+'\n'
        lst.append(expr)
        f.write(expr)

2.对拍代码：

点击查看代码

import sympy
from sympy import sin, cos
f1=open('C:/Users/Dell/Desktop/sj.txt')
f2=open('C:/Users/Dell/Desktop/res.txt')
r1=[]
for line in f1:
    for x in range(1,4):
        r=eval(line)
        r1.append(r)
r2=[]    
for line in f2:
    for x in range(1,4):
        r=eval(line)
        r2.append(r)
for i in range(len(r1)):
    if i % 150 == 0:
        print("comparing...",end='')
        print(i//150,end='')
        print("%")
    if abs(r1[i]-r2[i])>0.01:
        print("error")
        print(r1[i], "\n", r2[i], "\n", i//3)
print("done")

因为代码生成的是没有针对性的数据，而且限于自己的水平和时间，没有考虑前导0、求和函数和自定义函数，所以生成数据只是作为参考。

三、架构设计体验

3.1 无中生有——第一次作业架构设计

当时第一节OO课临下课时，老师的PPT放出题目简介，我一下子就感受到了作业的难度。指导书发布之后，我盯着指导书反反复复看了一个多小时，边看边思考架构和一些细节问题，但越想脑子越乱，陷于细节的泥潭中无法脱身。于是我索性放弃无谓的纠缠，先把表达式的预处理方法写好。写好之后，先前混杂着连续加减和空白字符的混乱表达式一下子变得干净清爽，我也得以继续集中注意力思考架构问题。

考虑到最多只存在一层括号，我很快想到，如果把表达式拆到括号在左右两端时，就可以将括号去掉。要达到这个目的，首先通过加减号将表达式拆成一个个项，再通过乘号将项拆成一个个因子。但我很快就发现了一个问题：如何区分括号中的加号和括号外的加号？仔细思考之后，我采用了一个比较取巧的方法：遍历字符串，将最外层的加号换成“@”号，减号换成“#”号。这样就能通过正则表达式将表达式拆开，拆乘号同理。

接下去就比较顺利了。先把表达式一直向下拆直到常数和x，然后在各类中实现calculate()方法，将底层运算结果向上传递，上层综合下层结果进行计算，最后在最上层用字符串化方法输出。虽然之后遇到了一些奇奇怪怪的小bug，但最后都算是比较顺利地解决了。

3.2 添砖加瓦——第一次作业到第二次的迭代

第二次作业相对于第一次添加了很多新的功能：求和函数、自定义函数、三角函数。本着步步为营，逐个突破的思想，我首先实现了对求和函数和自定义函数的替换。由于进行替换时可能出现i**2-->-1**2这样的情况，所以我将所有的替换都加上了括号。这样的话，不可避免地就要出现嵌套括号，如何处理嵌套括号呢？为了这个问题，我思考了很久。如果还是按照第一次作业逐层向下处理的思想，那必然会导致重构。出于自身的懒惰，我对重构是十分抗拒的。幸运的是，经过思考，我想到了一个差强人意的方法：寻找表达式内只含一层括号的表达式因子，把它提取出来进行处理，将处理结果进行替换。这时又有了一个问题：按数学意义，三角函数的括号是不能去除的，那如何在寻找子表达式时忽略三角函数的括号呢？经过思考，我又搬出了第一次作业定位最外层加减号的方法：特殊符号替换。结果上述处理，代码基本架构已经成型。

然后就是基项的修改。为了在基项中包含三角函数，我实现了三角函数类TrigoFunction，并在基项中添加了ArrayList<TrigoFunction> SinFunlist和ArrayList<TrigoFunction> CosFunlist两个属性。为了便于同类项合并，我还为TrigoFunction实现了Comparable接口并重写了compareTo()方法，使得同类项中三角函数排列顺序一致。

为了使输出长度最小化，我还对三角函数进行了一些力所能及的化简。首先是sin(0),cos(-1)这样的，很快就实现了化简。但我在化简1-sin(x)**2这样的表达式时遇到了不小的困难：匹配项很难精准识别。经过思考，我决定不识别匹配项，而是遇到sin(x)**2这样的项时，直接把它替换为1-cos(x)**2，然后尝试合并同类项，如果合并之后长度短于合并之前，则采用，否则不采用。依靠这种算法，我在强测中成功拿到了全部的性能分。

3.3 更上一层——第二次作业向第三次的迭代

第三次作业的迭代相对来说就比较简单了。主要就是两个新功能：自定义函数的嵌套调用和三角函数内容物的扩展。对于前一个功能，只需要循环替换自定义函数即可。而对于后一个功能，也只需要把TrigoFuntion的属性改为ArrayList<BaseTerm>，在构造函数中把内容物送进Polynomial类解析即可。唯一可能比较麻烦的是BaseTrem和TrigoFunctio类compareTo()方法的修改。由于这两个类是你中有我我中有你的，所以他们的compareTo()方法也必然是互相嵌套的。所以要是不把逻辑理清楚的话，很容易出现逻辑漏洞。

比较遗憾的是，在最后的输出优化中，我没有对三角函数进行充分的化简，导致了一定的性能分损失。不过总体来说我还是很满意了。

四、心得体会

总体上来说，第一单元的三次作业都完成的不错，我也学到了许多面向对象编程的方法和思维，更加熟练地掌握了Java语言。三次作业的bug一次比一次少，也算是我进步的体现吧。当然，这一单元的训练也让我认识到了自己的许多不足，比如思维仍然受到面向过程编程的影响、高内聚低耦合控制不充分等等。在之后的作业中我将针对这些问题不断进行改进。