Coursera机器学习——Recommender System测验
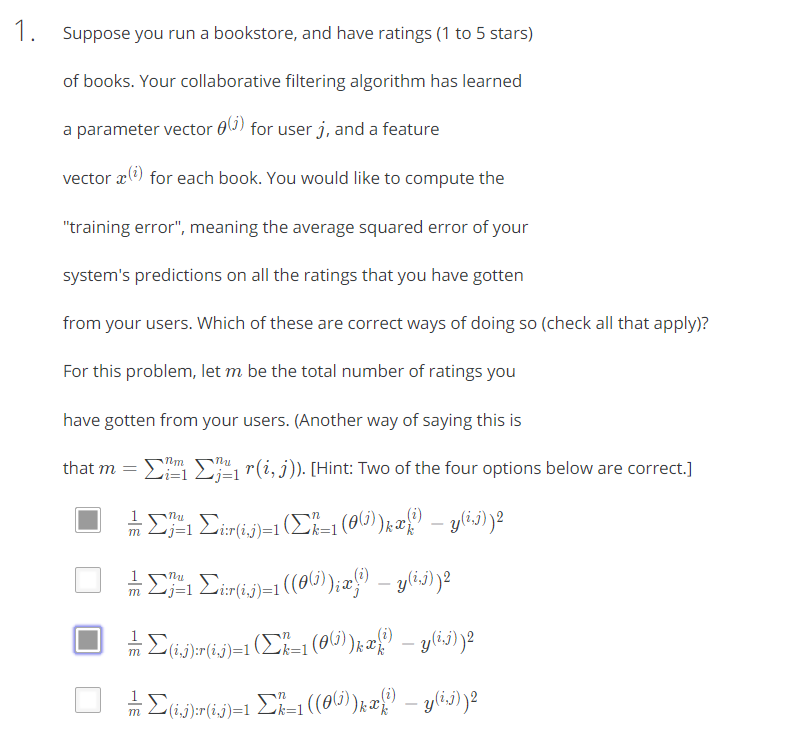
第一题本应该是基础题,考察Cost Function不同形式的表示方法,但却难住了我,说明基本概念掌握不够到位。
1. 在求和的部分,有两种可能,一种是(i,j)同时求和,即∑(i,j):r(i,j)=1,另一种是∑j=1nu∑i:r(i,j)=1或者∑i=1nu∑j:r(i,j)=1都可以。
2. 后面的部分,一是要注意括号的位置,如果是对K项Theta和X求和,必须是求和后的结果再减去y(i,j),而不要把y(i,j)也放入求和表达式中
3. 如果不是K项求和,说明使用向量的方法直接求Theta*X,那么此时Theta是转置的,上标有T符号存在

第二题是比较协同过滤和线性回归以及逻辑回归的不同使用场景
1. 选项A是想要得到一个书籍销售量与书籍评分之间的关系函数,这里使用线性回归最为恰当
2. 选项B我们得到有不同客户对款式和品牌的review信息,然后向顾客推荐,所以这里用协同过滤推荐很合适
3. 选项C是标准的协同过滤使用场景,我们有不同顾客对书的评分,然后给顾客推荐书籍
4. 选项D有一句很重要的关键句是and each client purchases at most 1 portrait. 所以不同用户对每幅作品的评分并没有重叠性,用协同过滤不能得到好的预测结果

第三题是说对于几个不同的评分系统能否对数据进行融合(三个系统的评分分数范围不同)
首先肯定是可以的,只是我们必须要先做特征放缩,再融合数据,否则直接融合会导致数据范围不同,影响推荐系统的表现

第四题是对协同过滤的考察
1. 选项A是说为了构建推荐系统,用户必须对训练集中所有的书籍进行评分。事实上如果有空缺的数据我们可以用均值填充
2. 选项B是说如果用户只对少部分产品打分,我们依然可以通过协同过滤构建一个推荐系统。是的,如上所说。只是性能可能不够好
3. 选项C是说我们需要使用梯度下降进行算法优化,不能使用高级算法,因为我们必须同时计算X和Theta。事实上,我们可以使用高级算法进行优化,也能做到同时 更新X和Theta

第五题是协同过滤算法实现的考察,因为我们只需要R(i,j) = 1的数据,所以若使用向量化方法实现需要进行预处理
1. 选项A是在求和计算结果前对矩阵和R做了点乘,所以R = 0的数据不会计入结果,可以√
2. 选项B先对矩阵A*B与R做点乘,在求和计算结果,也可以√
3. 选项C看似与A相同,但点乘改为普通矩阵乘法,就会导致结果错误,甚至两矩阵根本无法相乘
4. 选项D也是一样,将点乘改为普通乘法,不得行
还有一种写法也是可以的

总结:协同过滤适合于多特征,多用户(数据)的系统,当用户较少时,与线性回归效果大致相同,(当Nu = 1时,Jcost与线性回归完全相同),当特征较少时,协同过滤也不能较好的发挥它的效果


