[Data Structures] CF1928F Digital Patterns

线段树的练手好题。

Link：https://codeforces.com/problemset/problem/1928/F

Problem Statement

time limit per test: 2 seconds
memory limit per test: 256 megabytes

Anya is engaged in needlework. Today she decided to knit a scarf from semi-transparent threads. Each thread is characterized by a single integer — the transparency coefficient.

The scarf is made according to the following scheme: horizontal threads with transparency coefficients \(a_1, a_2, \ldots, a_n\) and vertical threads with transparency coefficients \(b_1, b_2, \ldots, b_m\) are selected. Then they are interwoven as shown in the picture below, forming a piece of fabric of size \(n \times m\), consisting of exactly \(nm\) nodes:

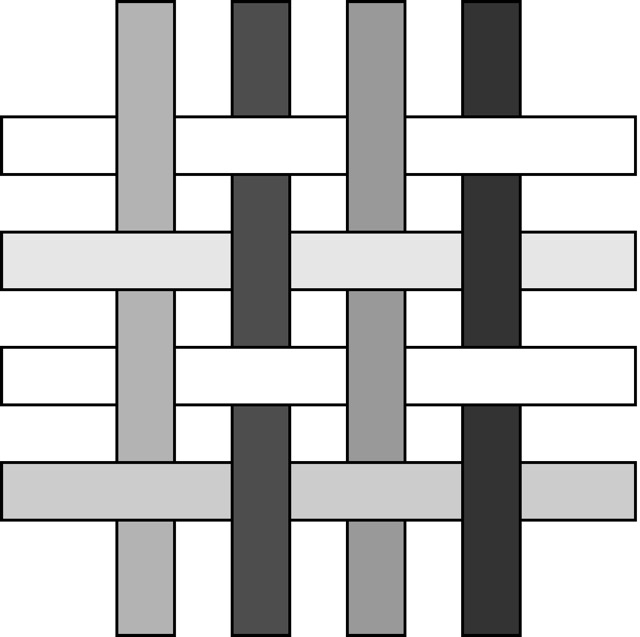Example of a piece of fabric for \(n = m = 4\).

After the interweaving tightens and there are no gaps between the threads, each node formed by a horizontal thread with number \(i\) and a vertical thread with number \(j\) will turn into a cell, which we will denote as \((i, j)\). Cell \((i, j)\) will have a transparency coefficient of \(a_i + b_j\).

The interestingness of the resulting scarf will be the number of its sub-squares\(^{\dagger}\) in which there are no pairs of neighboring\(^{\dagger \dagger}\) cells with the same transparency coefficients.

Anya has not yet decided which threads to use for the scarf, so you will also be given \(q\) queries to increase/decrease the coefficients for the threads on some ranges. After each query of which you need to output the interestingness of the resulting scarf.

\(^{\dagger}\)A sub-square of a piece of fabric is defined as the set of all its cells \((i, j)\), such that \(x_0 \le i \le x_0 + d\) and \(y_0 \le j \le y_0 + d\) for some integers \(x_0\), \(y_0\), and \(d\) (\(1 \le x_0 \le n - d\), \(1 \le y_0 \le m - d\), \(d \ge 0\)).

\(^{\dagger \dagger}\). Cells \((i_1, j_1)\) and \((i_2, j_2)\) are neighboring if and only if \(|i_1 - i_2| + |j_1 - j_2| = 1\).

Input

The first line contains three integers \(n\), \(m\), and \(q\) (\(1 \le n, m \le 3 \cdot 10^5\), \(0 \le q \le 3 \cdot 10^5\)) — the number of horizontal threads, the number of vertical threads, and the number of change requests.

The second line contains \(n\) integers \(a_1, a_2, \ldots, a_n\) (\(-10^9 \le a_i \le 10^9\)) — the transparency coefficients for the horizontal threads, with the threads numbered from top to bottom.

The third line contains \(m\) integers \(b_1, b_2, \ldots, b_m\) (\(-10^9 \le b_i \le 10^9\)) — the transparency coefficients for the vertical threads, with the threads numbered from left to right.

The next \(q\) lines specify the change requests. Each request is described by a quadruple of integers \(t\), \(l\), \(r\), and \(x\) (\(1 \le t \le 2\), \(l \le r\), \(-10^9 \le x \le 10^9\)). Depending on the parameter \(t\) in the request, the following actions are required:

• \(t=1\). The transparency coefficients for the horizontal threads in the range \([l, r]\) are increased by \(x\) (in other words, for all integers \(l \le i \le r\), the value of \(a_i\) is increased by \(x\));
• \(t=2\). The transparency coefficients for the vertical threads in the range \([l, r]\) are increased by \(x\) (in other words, for all integers \(l \le i \le r\), the value of \(b_i\) is increased by \(x\)).

Output

Output \((q+1)\) lines. In the \((i + 1)\)-th line (\(0 \le i \le q\)), output a single integer — the interestingness of the scarf after applying the first \(i\) requests.

Solution

首先考虑转化问题，考虑一个正方形 \((x, y), (x + d, y + d)\) 合法的条件是什么。如果对于任何的 \(i(x \leq i < x + d)\) 满足 \(a_{i} \neq a_{i + 1}\) 并且对于任何的 \(i(y \leq i < y + d)\) 满足 \(b_{i} \neq b_{i + 1}\)，那这个正方形就是满足条件的。

设长度为 \(L\) 且相邻元素（\(a\) 中）互不相同的区间数量为 \(A_L\)。设长度为 \(L\) 且相邻元素（\(b\) 中）互不相同的区间数量为 \(B_L\)。那么答案为 \(\displaystyle \sum_{i = 1}^{\max(n, m)}A_i \times B_i\)。

考虑计算 \(A, B\)。

考虑每个极长的区间 \([l, r]\) 满足对于任意的 \(i(l \leq i < r)\) 有 \(a_{i} \neq a_{i + 1}\)。那么其对 \(A_x\) 的贡献为 \(\max(0, r - l - x + 2)\)，正确性显然。对 \(B\) 的计算同理。

现在我们需要实现 \(3\) 种操作：

• 给 \(A[1 \sim x]\) 加 / 减一个首项为 \(x\)，公差为 \(-1\) 的等差数列。

• 给 \(B[1 \sim x]\) 加 / 减一个首项为 \(x\)，公差为 \(-1\) 的等差数列。

• 求 \(\displaystyle \sum_{i = 1}^{\max(n, m)}A_i \times B_i\)。

最重要的来了！线段树下传标记。

考虑维护 \(\displaystyle \sum_{i} A_i, \sum_{i} i \times A_i, \sum_{i} B_i, \sum_{i} i \times B_i, \displaystyle \sum_{i = 1}^{\max(n, m)}A_i \times B_i\)。

再考虑标记的形式，最后肯定可以规约到加上一个首项为 \(x\)，公差为 \(d\) 的等差数列。（因为一个首项为 \(x_1\)，公差为 \(d_1\) 的等差数列和一个首项为 \(x_2\)，公差为 \(d_2\) 的等差数列相加会得到一个首项为 \(x_1 + x_2\)，公差为 \(d_1 + d_2\) 的等差数列。正确性显然。再理解不了可以自己算。）

push_up 很简单，直接合并两个儿子的信息即可。

void push_up (int u) {
  ans[u] = ans[u << 1] + ans[u << 1 | 1];
  sum[u][0] = sum[u << 1][0] + sum[u << 1 | 1][0];
  sum[u][1] = sum[u << 1][1] + sum[u << 1 | 1][1];
  coef[u][0] = coef[u << 1][0] + coef[u << 1 | 1][0];
  coef[u][1] = coef[u << 1][1] + coef[u << 1 | 1][1];
  return ;
}

额外定义两个函数，就是求 \(\displaystyle \sum_{i = 0}^{n - 1}(x + di)\) 和 \(\displaystyle \sum_{i = 0}^{n - 1}i \times (x + di)\) 用的。具体可以展开式子然后用 \(\displaystyle \sum_{i = 1}^{n}i\) 和 \(\displaystyle \sum_{i = 1}^{n}i^2\) 的公式算。

考虑 apply 一个标记。显然 \(\displaystyle \sum_{i} A_i, \sum_{i} i \times A_i, \sum_{i} B_i, \sum_{i} i \times B_i\) 的值可以用上面的两个函数直接算出上述式子的变化量。考虑维护 \(\displaystyle \sum_{i = 1}^{\max(n, m)}A_i \times B_i\)：假设区间加的是 \(A\)，那么变化量一定是一个等差数列按位乘上一个 \(B\)，那么可以用 \(B\) 的信息推出变化量。具体见代码：

void apply (int u, ll l, ll r, ll push_tag, ll push_d, int k) {
  if (!push_tag && !push_d) return ;
  ans[u] += (push_tag - push_d) * sum[u][k ^ 1];
  ans[u] += push_d * coef[u][k ^ 1];
  coef[u][k] += (query2 (push_tag, push_d, r) - query2 (push_tag, push_d, l - 1));
  sum[u][k] += (query (push_tag, push_d, r) - query (push_tag, push_d, l - 1));
  tag[u][k] += push_tag;
  tagd[u][k] += push_d;
  return ;
}

push_down 就直接无脑 apply：

void push_down (int u, ll l, ll r) {
  ll mid = (l + r) >> 1;
  apply (u << 1, l, mid, tag[u][0], tagd[u][0], 0);
  apply (u << 1, l, mid, tag[u][1], tagd[u][1], 1);
  apply (u << 1 | 1, mid + 1, r, tag[u][0], tagd[u][0], 0);
  apply (u << 1 | 1, mid + 1, r, tag[u][1], tagd[u][1], 1);
  tag[u][0] = 0, tagd[u][0] = 0;
  tag[u][1] = 0, tagd[u][1] = 0;
  return ;
}

剩下的是线段树常规操作了。

现在只剩下一个问题了，怎么维护极长段的长度呢？我们可以拿一个 std :: set 动态记录一下相邻且相同的下标，相邻两个下标的差值就是极长段的长度。记得插入 \(1\) 和 \(n + 1\)。

因为每次修改 std :: set 只会变化 \(O(1)\) 个值。所以复杂度可以做到 \(O(n \log n)\)。但是大常数。

具体修改 \(A, B\) 序列的值可以通过树状数组 + 差分解决。

然后就做完了。

一些卡常技巧

把 \(\displaystyle \sum_{i = 1}^{n}i\) 和 \(\displaystyle \sum_{i = 1}^{n}i^2\) 都 \(O(n)\) 与处理一下。不然放到 push_down 里边先算会产生很多乘除运算，自然就常数很大了。

Code

难写。但是挺符合正常难度的 2F 定位的。

代码跑的比较慢，跑了 \(\symbfit{1575}\textbf{ ms}\)。

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/rope>
bool Mbe;
typedef long long ll;
std :: mt19937 rnd (std :: time (0));
template < class T > T gen (const T l, const T r) {return rnd () % (r - l + 1) + l;}
const double pi = std :: acos (-1);
template < class T > inline void read (T &val) {
  T x = 0;
  bool f = false;
  char c = std :: getchar ();
  for ( ; c < '0' || c > '9' ; c = std :: getchar ()) f |= (c == '-');
  for ( ; c >= '0' && c <= '9' ; c = std :: getchar ()) x = (x << 1) + (x << 3) + (c & 15);
  val = (!f) ? (x) : (-x);
  return ;
}
#define debug(fmt, ...) fprintf(stderr, fmt, ##__VA_ARGS__)
const ll hashmod1 = 2147483579, hashmod2 = 1610612741, hashmod3 = 805306457;
template < class T, class I > void chkmin (T &p, I q) {T q_ = q; p = std :: min (p, q_); return ;}
template < class T, class I > void chkmax (T &p, I q) {T q_ = q; p = std :: max (p, q_); return ;}
const int N = 3e5 + 25;
ll val[N][2];
namespace T {
  ll sum[N << 2][2], coef[N << 2][2];
  ll ans[N << 2];
  ll tag[N << 2][2], tagd[N << 2][2];
  void push_up (int u) {
    ans[u] = ans[u << 1] + ans[u << 1 | 1];
    sum[u][0] = sum[u << 1][0] + sum[u << 1 | 1][0];
    sum[u][1] = sum[u << 1][1] + sum[u << 1 | 1][1];
    coef[u][0] = coef[u << 1][0] + coef[u << 1 | 1][0];
    coef[u][1] = coef[u << 1][1] + coef[u << 1 | 1][1];
    return ;
  }
  ll query (ll x, ll d, ll n) {return n * x + val[n - 1][0] * d;}
  ll query2 (ll x, ll d, ll n) {
    return val[n][0] * (x - d) + val[n][1] * d;
  }
  void apply (int u, ll l, ll r, ll push_tag, ll push_d, int k) {
    if (!push_tag && !push_d) return ;
    ans[u] += (push_tag - push_d) * sum[u][k ^ 1];
    ans[u] += push_d * coef[u][k ^ 1];
    coef[u][k] += (query2 (push_tag, push_d, r) - query2 (push_tag, push_d, l - 1));
    sum[u][k] += (query (push_tag, push_d, r) - query (push_tag, push_d, l - 1));
    tag[u][k] += push_tag;
    tagd[u][k] += push_d;
    return ;
  }
  void push_down (int u, ll l, ll r) {
    ll mid = (l + r) >> 1;
    apply (u << 1, l, mid, tag[u][0], tagd[u][0], 0);
    apply (u << 1, l, mid, tag[u][1], tagd[u][1], 1);
    apply (u << 1 | 1, mid + 1, r, tag[u][0], tagd[u][0], 0);
    apply (u << 1 | 1, mid + 1, r, tag[u][1], tagd[u][1], 1);
    tag[u][0] = 0, tagd[u][0] = 0;
    tag[u][1] = 0, tagd[u][1] = 0;
    return ;
  }
  void update (int u, ll l, ll r, int x, int y, ll push_tag, ll push_d, int k) {
    if (x <= l && r <= y) {
      apply (u, l, r, push_tag, push_d, k);
      return ;
    }
    push_down (u, l, r);
    ll mid = (l + r) >> 1;
    if (x <= mid) update (u << 1, l, mid, x, y, push_tag, push_d, k);
    if (y > mid) update (u << 1 | 1, mid + 1, r, x, y, push_tag, push_d, k);
    push_up (u);
    return ;
  }
}
int n, m, q, M;
namespace A {
  ll c[N];
  void update (int u, ll x) {for (int i = u;i <= n; i += i & -i) c[i] += x; return ;}
  void modify (int l, int r, ll x) {update (l, x), update (r + 1, -x); return ;}
  ll query (int u) {ll ans = 0; for (int i = u;i > 0; i -= i & -i) {ans += c[i];} return ans;}
}
namespace B {
  ll c[N];
  void update (int u, ll x) {for (int i = u;i <= m; i += i & -i) c[i] += x; return ;}
  void modify (int l, int r, ll x) {update (l, x), update (r + 1, -x); return ;}
  ll query (int u) {ll ans = 0; for (int i = u;i > 0; i -= i & -i) {ans += c[i];} return ans;}
}
std :: set < int > st[2];
void modify (int k, ll x, ll d) {
  T :: update (1, 1, std :: max (n, m), 1, std :: max (-x, x), x, d, k);
  return ;
}
void insert (int k, int x) {
  if (!k && (x <= 1 || x > n)) return ;
  if (k && (x <= 1 || x > m)) return ;
  if (st[k].count (x)) return ;
  st[k].insert (x);
  auto l = st[k].find (x);
  auto r = st[k].find (x);
  l --, r ++;
  int L = *l, R = *r;
  modify (k, -(R - L), 1);
  modify (k, x - L, -1);
  modify (k, R - x, -1);
  return ;
}
void erase (int k, int x) {
  if (!k && (x <= 1 || x > n)) return ;
  if (k && (x <= 1 || x > m)) return ;
  if (!st[k].count (x)) return ;
  auto l = st[k].find (x);
  auto r = st[k].find (x);
  l --, r ++;
  int L = *l, R = *r;
  modify (k, -(x - L), 1);
  modify (k, -(R - x), 1);
  modify (k, R - L, -1);
  st[k].erase (x);
  return ;
}
bool Med;
signed main () {
  debug ("%.8lf MB\n", (&Mbe - &Med) / 1048576.0);
  read (n), read (m), read (q);
  for (ll i = 1;i <= std :: max (n, m); ++ i) {
    val[i][0] = val[i - 1][0] + i;
    val[i][1] = val[i - 1][1] + i * i;
  }
  st[0].clear (), st[1].clear ();
  ll las = -2e9;
  st[0].insert (1), st[0].insert (n + 1);
  for (int i = 1;i <= n; ++ i) {
    ll x;
    read (x);
    if (x == las) st[0].insert (i);
    las = x;
    A :: modify (i, i, x);
  }
  las = -2e9;
  st[1].insert (1), st[1].insert (m + 1);
  for (int i = 1;i <= m; ++ i) {
    ll x;
    read (x);
    if (x == las) st[1].insert (i);
    las = x;
    B :: modify (i, i, x);
  }
  las = -1;
  for (auto u : st[0]) {
    if (las != -1) modify (0, u - las, -1);
    las = u;
  }
  las = -1;
  for (auto u : st[1]) {
    if (las != -1) modify (1, u - las, -1);
    las = u;
  }  
  printf ("%lld\n", T :: ans[1]);
  while (q --) {
    int o, l, r;
    ll w;
    read (o), read (l), read (r), read (w);
    if (!w) {
      printf ("%lld\n", T :: ans[1]);
      continue;
    }
    o --;
    if (!o) {
      A :: modify (l, r, w);
      if (A :: query (l) == A :: query (l - 1)) insert (o, l);
      else erase (o, l);
      if (A :: query (r) == A :: query (r + 1)) insert (o, r + 1);
      else erase (o, r + 1);
    }
    else {
      B :: modify (l, r, w);
      if (B :: query (l) == B :: query (l - 1)) insert (o, l);
      else erase (o, l);
      if (B :: query (r) == B :: query (r + 1)) insert (o, r + 1);
      else erase (o, r + 1);
    }
    printf ("%lld\n", T :: ans[1]);
  }
  debug ("%.8lf ms\n", 1e3 * clock () / CLOCKS_PER_SEC);
  return 0;
}
// g++ "a.cpp" -o a -std=c++14 -O2 -Wall -Wextra -Wshadow
// check! no inline! (except fastIO)