AtCoder Regular Contest 合集 I
[ARC169D] Add to Make a Permutation
\(\text{Time Limit: 2 sec / Memory Limit: 1024 MB / Difficulty: }\color{red}2812\)
Problem Statement

Constraints
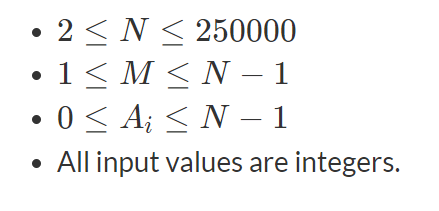
Solution & Code
考虑操作时不 \(\bmod n\)。
设最后操作完后的序列为 \(A' = (a'_1, a'_2, \dots, a'_n)\),如果满足条件,那么有:
-
对于任意的 \(1 \leq i \leq n\),有 \(a'_i \geq a_i\)。
-
\(B = (a'_1 \bmod n, a'_2 \bmod n, \dots, a'_n \bmod n)\) 是一个 \(0 \sim n - 1\) 的排列。
-
\(\displaystyle \sum_{i = 1}^{n}(a'_i - a_i) \bmod m = 0\)。
-
\(\displaystyle \max_{i = 1}^{n}(a'_i - a_i) \leq \dfrac{\displaystyle \sum_{i = 1}^{n}(a'_i - a_i)}{m}\)
这些条件是充要条件。
Conclusion. 一定有一个最优解形如 \(A' = (f, f + 1, \dots, f + n - 1)\),其中 \(A'\) 经过了排序。显然 \(A'_1\) 一定对应 \(A\) 中最小的数,\(A'_2\) 一定对应 \(A\) 中第 \(2\) 小的数。以此类推。这里将 \(\symbfit{A}\) 和 \(\symbfit{A'}\) 都重新从小到大排序。
Proof. 考虑调整法。
若现在 \(a'_n - a'_1 \geq n\),那么考虑 \(a'_1 \leftarrow a'_n - n, a'_n \leftarrow a'_1 + n\)。
-
因为 \(a'_n - a'_1 \geq n, a_n - a_1 < n\),又因为 \(a'_n \geq a_n, a'_1 \geq a_1\),可得 \(a'_n - a_1 \geq n\),即 \(a'_n - n \geq a_1\);还可得 \(a_n < a'_1 + n\),所以满足第一个条件。
-
\(A'\) 中所有的数的 \(\bmod n\) 的值没有发生变化,依然合法。所以满足第二个条件。
-
\(\displaystyle \sum_{i = 1}^{n}(a'_i - a_i)\) 没有发生变化,依然合法。所以满足第三个条件。
-
因为操作后变化的只有 \(a'_1, a'_n\),所以变化的只可能有 \(a'_1 - a_1\) 和 \(a'_n - a_n\)。由 \(a'_n - a'_1 \geq n\) 可知 \(a'_n \geq a'_1 + n\) 即 \(a'_n - a_n \geq a'_1 + n - a_n\),所以 \(a'_n - a_n\) 的值没有变大。因为 \(a'_n - a_n - a_1 < a'_n - a_n\) 可得 \(a'_n - a_n - a_1\) 一定不会使 \(\displaystyle \max_{i = 1}^{n}(a'_i - a_i)\) 变大,前者也是。所以满足第四个条件。
所以现在只需要确定最小的 \(f\) 满足条件。
-
\(a'_i = f + i - 1 \geq a_i\) 可得 \(f \geq a_i - i + 1\)。
-
第二个条件自动满足。
-
第三个条件在确定了 \(f\) 的下界后不断的试 \(m + 1\) 次即可,根据抽屉原理可得一定出现了循环节,如果有 \(f\) 满足就满足了,否则就不满足。
-
第四个条件如果不满足就不断增大 \(f\) 直到满足,这里可以快速计算出。具体见代码。
代码:https://atcoder.jp/contests/arc169/submissions/49594743
[ARC171B] Chmax
\(\text{Time Limit: 2 sec / Memory Limit: 1024 MB / Difficulty: }\color{cyan}1374\)
Problem Statement

Constraints
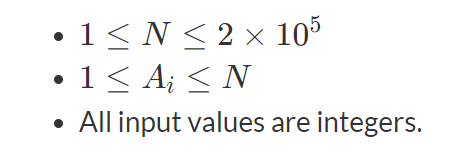
Solution & Code
首先有一个结论就是,对于任意一个 \(1 \sim n\) 的排列 \(p\),对于每一个 \(1 \leq i \leq n\),连有向边 \(i \to p_i\),那么最终的图就是若干个不相交的环。设 \(a_i = v\) 的所有 \(i\) 组成的集合为 \(S_v\)。
- 对于任意的 \(\symbfit{1 \leq i \leq n}\) 有 \(\symbfit{a_i \geq i}\)。 根据题意显然。
本题的 和法解 有以下性质:
首先建图。
-
\(\symbfit{S_v}\) 中的点一定在一个环里面。 不然不会最终的值都是 \(v\)。
-
\(\symbfit{S_v}\) 中不会有 \(\symbfit{> v}\) 的点。 不然不合法。
-
\(\symbfit{S_v}\) 中的点按从小到大的顺序成链,链尾(链尾定义为 chkmax 操作结束的节点)必定为 \(\symbfit{v}\)。 如果 \(S_v\) 里面的点兵分两路那就会产生 \(v\) 的 \(2\) 个入度,不合法。否则那就会掺和其他的点在一条链上,会导致两个 \(a\) 值不同的点的 \(a\) 值相同,那肯定不合法。链尾如果不是 \(v\) 那么会变成 \(\neq v\) 的数,不合法。
-
\(\symbfit{S_v}\) 中必然会有 \(\symbfit{v}\),如果没有那么 \(B_v\) 会变成更大的数,那么 \(S_v\) 也会随链成为更大的数(参考上一条性质),就不合法了。
所以只有 \(S_v\) 中只有 \(p_v\) 的值不确定,其他的 \(p\) 值都已经确定。那就把所有的 \(v\) 拎出来,从小到大乘法原理和剩下的数匹配即可。
代码:https://atcoder.jp/contests/arc171/submissions/50010937
[ARC171C] Swap on Tree
\(\text{Time Limit: 2 sec / Memory Limit: 1024 MB / Difficulty: }\color{gold}2244\)
Problem Statement

Constraints
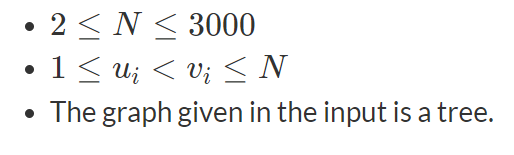
Solution & Code
首先考虑最终被断掉的边,一个结论是,如果被断掉的边集不同那么最终形成的排列一定不同,如果 \((u, v)\) 这条边 \(E_1\) 中断掉了但 \(E_2\) 中没有断掉,那么在 \(E_2\) 中 \((u, v)\) 两边的连通块内的数永远不会发生交换,而 \(E_1\) 中会发生一次交换,最后形成的排列一定不同。
那么考虑一个边集 \(E\),最后会产生多少种排列。容易发现对于一个节点 \(u\),其连出去的边在断边的顺序中不同,其产生的排列也不同。考虑以 \(u\) 为根的情况,若 \(\text{deg}(u) < 2\) 那么自动满足。现在只考虑 \(\text{deg}(u) \geq 2\) 的情况,容易发现只有断边才有可能让子树内的数与外界交换,所以如果不断掉与父亲的边那么子树内的数其实是封闭的,设按 \((o_1, o_2, \dots, o_m)\) 的顺序与 \(u\) 断边,那么进入 \(o_1\) 子树的其他数只有可能是 \(a_u\),进入 \(o_2\) 子树内的其他数只有可能来自 \(o_1\) 子树,以此类推,不同的断边顺序会导致答案不同,那么只需要考虑一个点连出去的边在断边顺序里的相对顺序即可,所以一个边集对答案的贡献为 \(\displaystyle \prod_{i = 1}^{n}\text{deg}(i)!\),其中 \(\text{deg}(i)\) 表示 \(\displaystyle \sum_{(u, v) \in E}[u = i] + \sum_{(u, v) \in E}[v = i]\)。
现在考虑 DP,设 \(f_{u, i}\) 表示 \(u\) 与 \(i\) 个 \(u\) 的儿子有连边的贡献(\(u\) 的子树内),可以枚举每个儿子 \(v\),再枚举 \(j\),有转移:
最终的答案就是 \(\displaystyle \sum_{i = 0}^{n - 1}f_{root, i}\),其中 \(root\) 为树根。
代码:https://atcoder.jp/contests/arc171/submissions/50020042
[ARC171D] Rolling Hash
\(\text{Time Limit: 2 sec / Memory Limit: 1024 MB / Difficulty: }\color{gold}2377\)
Problem Statement

Constraints
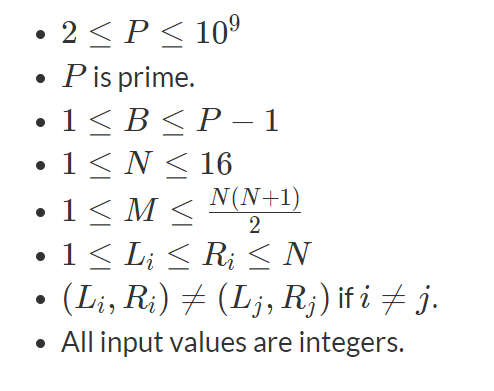
Solution & Code
设 \(C_i = \text{hash}(x_i, x_{i + 1}, \dots, x_n) = \left(\displaystyle \sum_{j = i}^{n}x_jB^{n - j}\right) \bmod P(1 \leq i \leq n + 1)\)。
考虑 \(\text{hash}(x_L, x_{L + 1}, \dots, x_R)\) 的表示:
因为 \(P\) 是质数,那么 \(ab \bmod P = 0\) 等价于 \(a \bmod P = 0\) 或 \(b \bmod P = 0\),证明显然。
根据上面的引理,\(B^{R-n} \bmod P = 0\) 需要 \(B \bmod P = 0\),而题面保证了 \(B \neq 0\),所以 \(\text{hash}(x_L, x_{L + 1}, \dots, x_R) = 0\) 等价于 \(C_{L} = C_{R + 1}\),因为 \(P\) 是质数所以 \(B\) 的逆元总是存在,所以可以根据 \(C\) 算出唯一的 \(A\),现在问题转化为给定 \((L_1, R_1), (L_2, R_2), \dots, (L_m, R_m)\),然后对于任意的 \(1 \leq i \leq m\),连无向边 \((L_i, R_i + 1)\),最后形成一张 \(n + 1\) 个点的无向图,要求给这 \(n + 1\) 个点染上 \(P\) 种颜色使得对于任意一条边 \((u, v)\) 满足 \(u, v\) 的颜色不同。首先如果 \(P \geq n + 1\) 那就直接用 \(n + 1\) 种颜色染色即可。发现同一种颜色的点在原图中是一个独立集,可以 \(O(2^nm)\) 预处理出所有的独立集,设 \(f_S\) 表示集合 \(S\) 中的点最少由 \(f_S\) 个独立集合并而成,转移可以 \(O(3^n)\) 枚举子集实现。具体见代码。如果 \(f_{\{1, 2, \dots, n\}} \leq P\) 那么有解,否则无解。

