五一 NOI 数学听课笔记
注:本文不写证明。
花絮:真·sigma: ,真·abc:
,真·abc: ,
,
一、剩余类环
记号:
加法逆元:
乘法逆元:
费马小定理
Euler's Theorem / 费马小定理推广:
Quiz
计算:
使用 Euler's Theorem 需要算出
Lemma 1:若
Lemma 2:若
定理:若
Example
HW1:
二、扩展 Euclid
此算法可以计算形如
记
方程的解,所以
整理得到:
所以
三、原根
对于正整数
另一个说法:
i.e. 在
结论:
在
Problem
给定
考虑随机化,单次的成功率是
原根判定定理:设
指标
定义:记
这也被称为离散对数。
BSGS, Baby Step Giant Step 算法
令
那么我们枚举
Extend BSGS 算法
给定
注意:
若
对于:
两边同时除以
然后换元:
得到:
这样一直迭代下去,直到无解或者可以使用 BSGS 解决。
最终的式子变成:
此时
二次剩余
求
结论:设
三次剩余
继续推广:
若
更一般的,若
若
一般二次同余式
求根公式:
配方:
四、中国剩余定理
已知
其中
当
五、数论函数
定义
定义
结论:
Mobius 函数
定义:
Dirichlet 卷积
定义:令
称
性质:
定理:若
观察:
说明
而
则说明
Mobius 反演
Example 1
Example 2
六、生成函数

Example 1

Example 2

Example 3



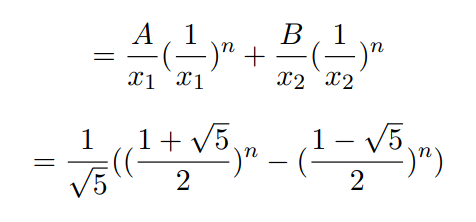
Example 4
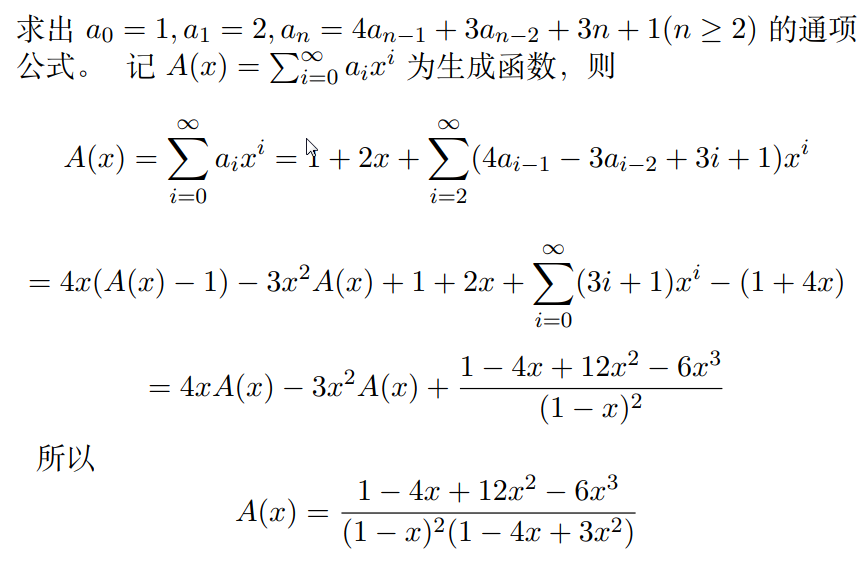

Example 5

Solution 待补充。
Example 6

Solution 1
我们考虑将左括号数量看成横坐标,右括号数量看成纵坐标,将括号序列看成路径,那么在任何时刻右括号数量不能超过左括号数量(这就是一个合法的括号序列)
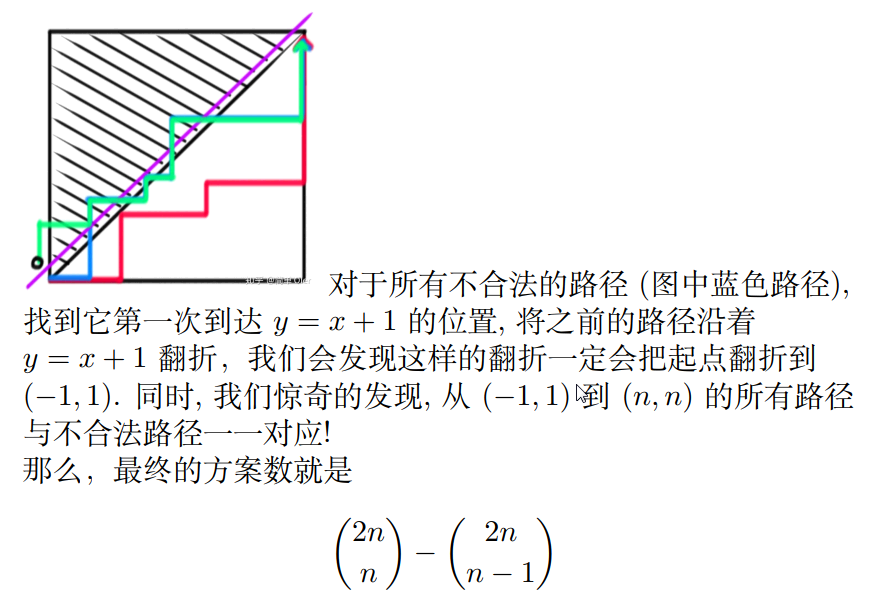
Solution 2



七、Stirling 数
第一类 Stirling 数

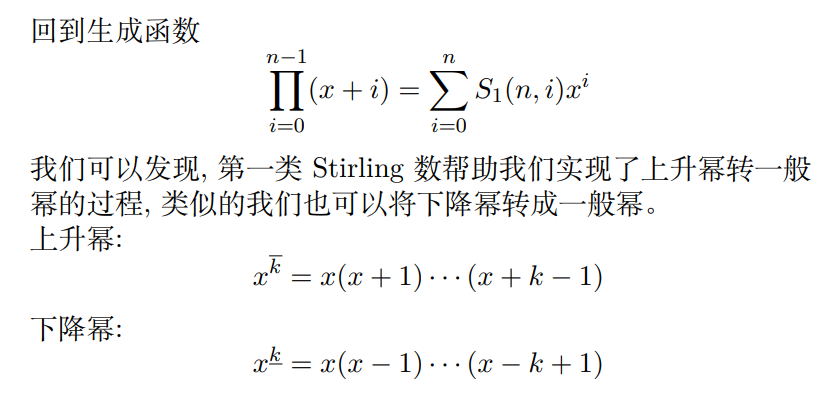
第二类 Stirling 数


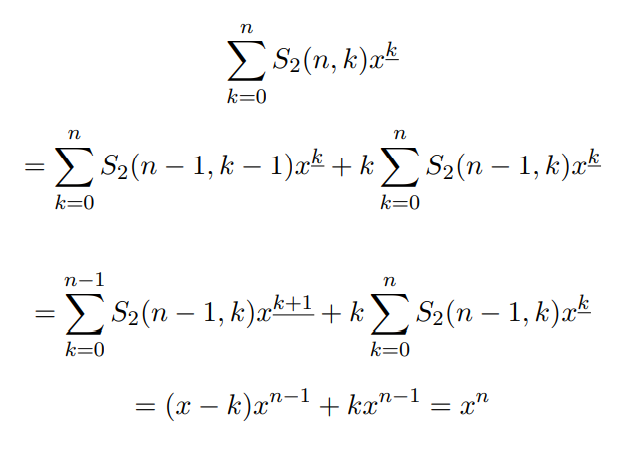

八、群论


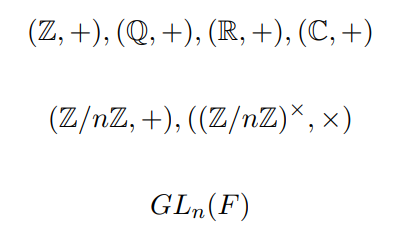
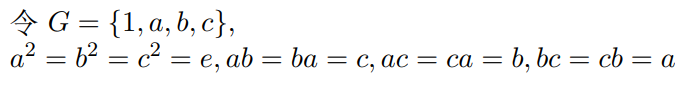

置换群

生成元

元素的阶

子群

陪集

陪集定理

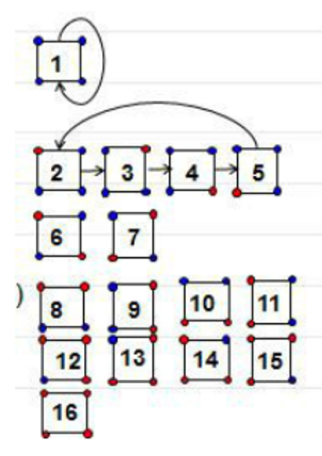
群作用

Example

轨道稳定集定理

Example

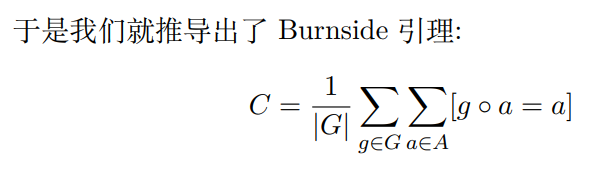
九、行列式
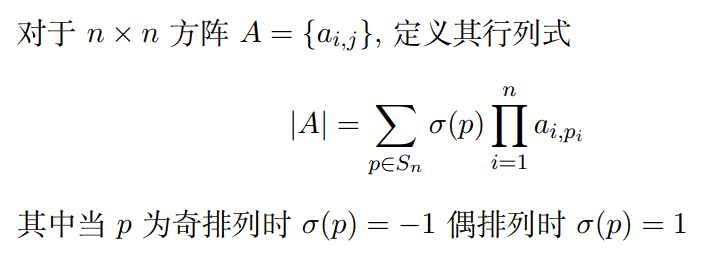



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义