统筹学步骤
确定目标
制定方案
建立模型
制订解法
关键路径法CPM
关键路径:在网络活动图AOE中,顶点到结束点最长的路径。
关键活动:在关键路径上的活动是关键活动
网络优化
时间优化:根据计划进度缩短完成时间。
时间资源优化:在合理利用资源并缩短工期。
时间费用优化:减少时间和费用。
极限时间:减少到的最短时间
直接费用率:(极限时间的直接费用-正常时间的直接费用)/(正常时间-极限时间)
网络实例
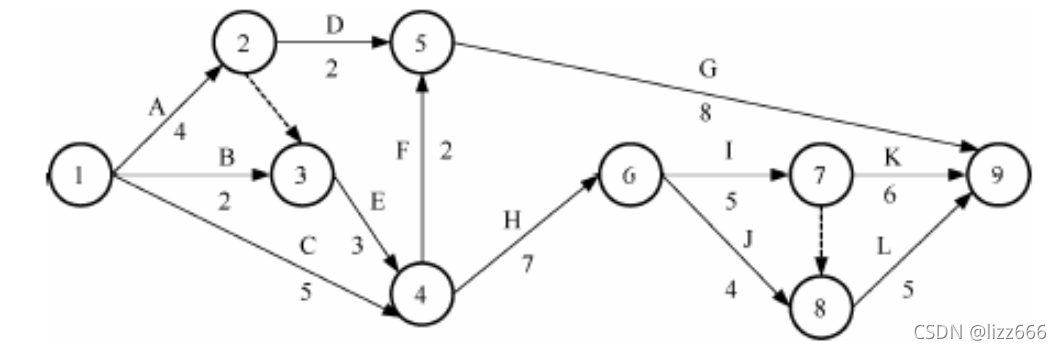
题:假设某信息系统开发工程合同工期为 25 个月,承建单位编制的网络计划图如图所示
该网络计划能否满足合同工期要求?为确保工程按期完工,哪些工作应作为重点对象?
当该计划执行 7 个月后,经监理工程师检查发现,工作 C 和 D 已完成,而 E 将拖后 2 个月。当计划执行到第 7 个月后,工作 E 的实际进度是否影响总工期?如果实际进度确定影响到总工期,为保证总工期不延长对原进度计划的调整方案有哪些?
如果承建单位提出采用压缩某些工作持续时间,对原计划进行调整以保证工期不延长,各工作的直接费用率与极限时间如表所示。在不改变各工作逻辑关系的前提下,原进度计划的最优调整方案是什么?此时直接费用将增加多少万元?
工程过程
F
G
H
I
J
K
L
直接费用率
-
10
6
4.5
3.5
4
4.5
极限时间-月
2
6
5
3
1
4
3
正常时间
2
8
7
5
4
6
5
图中有2条虚线表示需活动,不占用资源。关键路径为A-E-H-I-K,长度25,正好与合同周期一致,满足合同要求,因此需要对AEHIK五个工作作为重点对象。
因为E在关键路径上,所有会导致总工期延长2个月;为保证总空气不延长,有2中调整方法,一是改变某些工作之间的逻辑关系,二是缩短某些工作的时间。
需要调整关键路径上的A、E、H、I、K、工作,因为已经到了第7个月,因此A不在可调整范围内,另外E不在压缩表中,因此只能调整H、I、K这三个工作,而在表中K的直接费用率最小,且极限时间可以减少2个月,正好满足需要。但是K压缩1个月后关键路径会发生变化,AEHIK和AEHIL都是关键路径,此时只能压缩I工作,所以I和K各压缩一个月,费用为4+4.5=8.5万元。
线性规划
概念:研究在有限资源条件下,如何有效的使用资源达到预定目标的数学方法,也是在一组约束条件下寻找目标函数的极值问题。
求极大(或极小)值的模型:
在上述条件下,求x1,x2,...xn。使满足表达式极大(或极小)值z=c1x1+c2x2+..+cnxn
图解法
题:某工厂在计划期内要安排生产 I、II 两种产品,已知生产单位产品所需的设备台时及 A、B 两种原料的消耗,如表所示
I II 总数
设备
1
2
8台时
原材料A
4
0
16kg
原材料B
0
4
12kg
该工厂每生产一件产品 I 可获利 2 元,每生产一件产品 II 可获利 3 元,问应该如何安排计划使该工厂获利最多?
解:设 x1,x2 分别表示在计划期内产品 I、II 的产量,因为设备的有效台时是 8,这是一个限制产量的条件,所以在确定产品 I、II 的产量时,要考虑不超过设备的有效台时数,其中产品I需要1台设备,产品II需要2台设备,即可用不等式表示为:x1+2*x2≤8。
同理,因原料 A、B 的限量,可以得到以下不等式:
该工厂的目标是在不超过所有资源限制的条件下,如何确定产量 x1,x2 ,以得到最大的利润。若用 z 表示利润,这时 z =2*x1 +3*x2 。综上所述,该计划问题可用数学模型表示为:目标函数:最大z = 2*x1 + 3*x2
约束条件:x1 +2*x2 ≤8、4*x1 ≤16、4*x2 ≤12、x1、x2≥ 0。
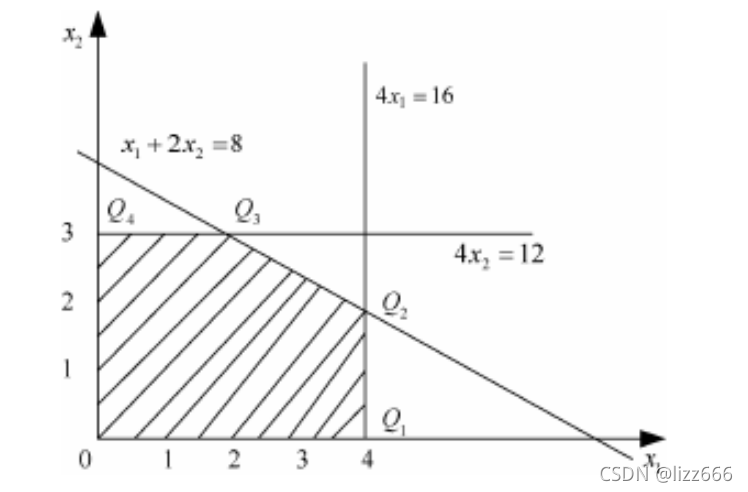
在以 x1,x2 为坐标轴的直角坐标系中,非负条件 x1, x2 ≥0 是指第一象限。上述每个约束条件都代表一个半平面。例如,约束条件 x1 + 2*x2 ≤8 代表以直线 x1 + 2*x2 ≤ 8 为
分析目标函数 z = 2*x1 +3*x2 在坐标平面上它可表示以 z 为参数,-2/3 为斜率的一族平行线:
位于同一直线上的点,具有相同的目标函数值,因此称为等值线。当 z 值由小变大时,直线沿其法线方向向右上方移动。当移动到 Q2 点时,使 z 值在可行域边界上实现最大化,这就得到了本题的最优解 Q2,Q2 点的坐标为(4,2)。经过计算,可以得出 z=14。
这说明该厂的最优生产计划方案是:生产 4 件产品 I,2 件产品 II,可得最大利润为 14 元。
决策论模型
面向决策结果:过程为确定目标>收集信息>提出方案>方案选择>决策
面向决策过程:阶段为预决策>决策>决策后
决策模型构成要素
决策者:个人、委员会或组织,一般为领导者或群体
可供选择的方案、行动或策略
衡量选择方案的准则:包括目的、目标、属性、正确性的小组,具有单一准则或多准则。
事件:不为决策者锁控制的客观存在的将要发生的状态。
每一事件的发生将产生的某种结果:如收益或者损失。
决策者的价值观:如决策者对货币额或不同风险的主观价值。
不确定性决策准则
悲观主义准则
乐观主义准则
折中主义准则
等可能准则
后悔值准则
不确定性决策准则实例
题:某公司需要根据下一年度宏观经济的增长趋势预测决定投资策略。宏观经济增长趋势有不景气、不变和景气 3 种,投资策略有积极、稳健和保守 3 种,各种状态的收益如表所示。
投资策略\经济趋势预测 不景气 不变 景气
积极
50
150
500
稳健
150
200
300
保守
400
250
200
乐观主义准则,追求最大值,最大值为收益值500,所以采取积极投资策略。
悲观主义准则,追求最小值中的最大值,积极策略最小值50,稳健策略最小值150,保守策略最小值200,选择其中最大值200,所以采取保守策略。
折中主义准则,根据值折中系数a,计算公式:cvi=α*max{aij}+(1−α)*min{aij},其中0≤α≤1,即用每个决策方案在各个自然状态下的最大效益值乘以 α,再加上最小效益值乘以 1−α。然后再比较 cvi,从中选择最大者。显然,折中主义准则的结果取决于α的选择。α接近于1,则偏向于乐观;α接近于 0,则偏向于悲观。
等可能准则,当决策者无法事先确定每个自然状态出现的概率时,就可以把每个状态出现的概率定为 1/n(n 是自然状态数),然后按照最大期望值准则决策。也就是说,把一个不确定型决策转换为风险决策。
后悔值准则,将每个自然状态的最大收益值作为理想目标,然后将最大值与当前值相减的到后悔值,然后在每个策略的最大后悔值中选取最小值后悔值。可生产后悔值表,其中积极策略中最大后悔值为350,稳健最大后悔值为250,保守最大后悔值为300,再其中250位最小后悔值,所以采取稳健策略。
投资策略\经济趋势预测 不景气 不变 景气
积极
400-50=350
250-150=100
500-500=0
稳健
400-150=250
250-200=50
500-300=200
保守
400-400=0
250-250=0
500-200=300
风险决策
概念:决策者对客观情况不甚了解,但对将要发生的各种事件的概率是已知的。一般采取期望值最为决策准则。
风险决策准则
最大期望收益决策准则EMV:决策矩阵的各元素代表“策略-事件”对的收益值,先计算各策略的期望收利益值 ,然后从这些期望收益值中选取最大者,以它对应的策略为决策者应选择的决策策略。
最小机会损失决策准则EOL:决策矩阵的各元素代表“策略-事件”对的损失值,各事件发生的概率为,先计算各策略的期望损失值,然后从这些期望收益值中选取最小
风险决策实例
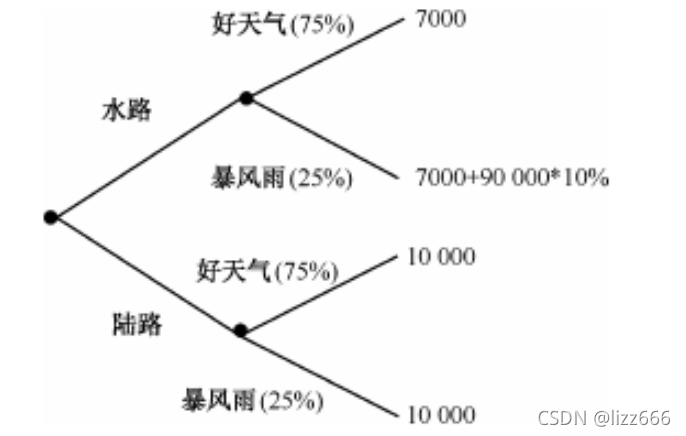
题:某电子商务公司要从 A 地向 B 地的用户发送一批价值为 90000 元的货物。从 A 地 到 B 地有水、陆两条路线。走陆路时比较安全,其运输成本为 10000 元;走水路时一般情况下的运输成本只要 7000 元,不过一旦遇到暴风雨天气,则会造成相当于这批货物总价值的 10%的损失。根据历年情况,这期间出现暴风雨天气的概率为 1/4,那么该电子商务公司该如何选择呢?
解:决策树如图
走水路时,成本为 7000 元的概率为 75%,成本为 16 000 元的概率为25%,因此,走水路的期望成本为(7000×75%)+(16000×25%) =9250(元);
走陆路时,其成本为(10 000×75%)+(10 000×25%)=10000(元)。
所以,走水路的期望成本小于走陆路的成本,应该选择走水路。
对策论
概念:也称为竞赛论或博弈论,是研究具体竞争性现象的数学理论和方法,大到国际谈判、政治较量,小到日常生活算计,都是对策论的研究对象。
对策论实例
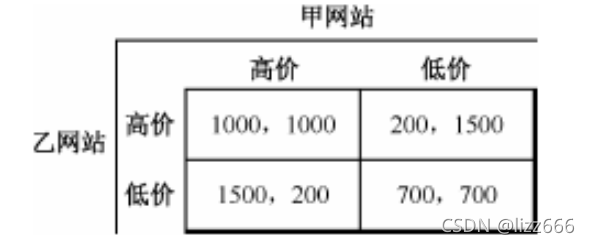
题:甲、乙两个独立的网站主要靠广告收入来支撑发展,目前都采用较高的价格销售广告。这两个网站都想通过降价争夺更多的客户和更丰厚的利润。假设这两个网站在现有策略下各可以获得 1000 万元的利润。如果一方单独降价,就能扩大市场份额,可以获得1500 万元利润,此时,另一方的市场份额就会缩小,利润将下降到 200 万元。如果这两个网站同时降价,则他们都将只能得到 700 万元利润。那么,这两个网站的主管各自经过独立的理性分析后,决定采取什么策略呢?
解:赢得矩阵
假设乙网站采用高价策略,那么甲网站采用高价策略得 1000 万元,采用低价策略得 1500 万元。因此,甲网站应该采用低价策略;
如果乙网站采用低价策略,那么甲网站采用高价策略得 200 万元,采用低价策略得 700 万元,因此,甲网站也应该采用低价策略。
采用同样的方法,也可分析乙网站的情况,也就是说,不管甲网站采取什么样的策略,乙网站都应该选择低价策略。因此,这个博弈的最终结果一定是两个网站都采用低价策略,各得到 700 万元的利润。
这个对策是一个非合作对策问题,且两个局中人都肯定对方会按照个体行为理性原则决策,因此,虽然双方采用低价策略的均衡对双方都不是理想的结果,但因为两个局中人都无法信任对方,都必须防备对方利用自己的信任(如果有的话)谋取利益,所以双方都会坚持采用低价,各自得到 700 万元的利润,各得 1000 万元利润的结构是无法实现的。即使两个网站都完全清楚上述利害关系,也无法改变这种结局。
数学建模
概念:当需要从定量的角度分析和研究一个实际问题时,人们就要在深入调查研究、了解对象信息、作出简化假设、分析内在规律等工作的基础上,用数学的符号和语言,把它表述为数学式子,也就是数学模型,然后用通过计算得到的模型结果来解释实际问题,并接受实际的检验。这个建立数学模型的全过程就称为数学建模。
数学建模是一种数学的思考方法,是运用数学的语言和方法,通过抽象和简化,建立能近似刻画并解决实际问题的模型的一种强有力的数学手段。
数学模型是客观世界中的实际事物的一种数学简化,它常常是以某种意义上接近实际事物的抽象形式存在的,但它和真实的事物有着本质的区别。
数学建模形式
目标的评价准则:U=f(xi,yi,ξk)
约束条件:g(xi,yi,ξk)≥0
xi为可控变量,yi为已知参数,ξk为随机因素
目标的评价准则一般要求达到最佳(最小或最大)、适中、满意等。准则可以是单一的,也可以是多个的。约束条件可以没有也可有多个。
当 g 是等式时,即为平衡条件。
当模型中无随机因素时,称它为确定性模型,否则为随机模型。
随机模型的评价准则可用期望值、方差表示,也可用某种概率分布来表示;
当可控变量只取离散值时,称为离散模型,否则称为连续模型。
也可按使用的数学工具,将模型分为代数方程模型、微分方程模型、概率统计模型、逻辑模型等;
若用求解方法来命名时,有直接最优化模型、数字模拟模型、启发式模型等;
也有按用途来命名的,例如,分配模型、运输模型、更新模型、排队模型、存储模型等;
还可以用研究对象来命名,例如,能源模型、教育模型、军事对策模型、宏观经济模型等。
数学建模的过程
模型准备:了解问题的实际背景,明确其实际意义,掌握对象的各种信息。用数学语言来描述问题。
模型假设:根据实际对象的特征和建模的目的,对问题进行必要的简化,并用精确的语言提出一些恰当的假设。
模型建立:在假设的基础上,利用适当的数学工具来刻画各变量之间的数学关系,建立相应的数学结构。只要能够把问题描述清楚,尽量使用简单的数学工具。
模型求解:利用获取的数据资料,对模型的所有参数作出估算。
模型分析:对所得的结果进行数学上的分析。
模型检验:将模型分析结果与实际情形进行比较,以此来验证模型的准确性、合理性和适用性。如果模型与实际较吻合,则要对计算结果给出其实际含义,并进行解释。如果模型与实际吻合较差,则应该修改假设,再次重复建模过程。
模型应用:应用方式因问题的性质和建模的目的而异。
数学建模的方法
直接分析法:根据对问题内在机理的认识,直接构造出模型。
类比法:根据类似问题的模型构造新模型。
数据分析法:通过试验,获得与问题密切相关的大量数据,用统计分析方法进行建模。
构想法:对将来可能发生的情况给出逻辑上合理的设想和描述,然后用已有的方法构造模型,并不断修正完善,直至用户比较满意为止。
posted @
2023-12-01 16:22
R-Bear
阅读(
350 )
评论()
收藏
举报
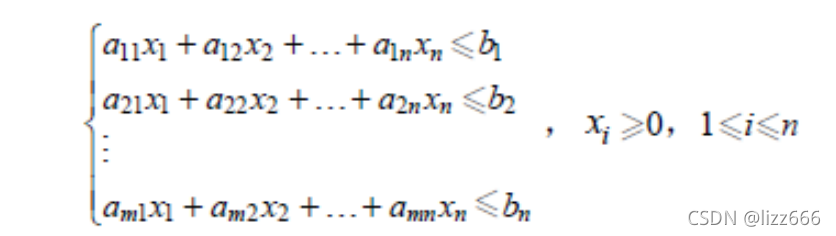
![]()


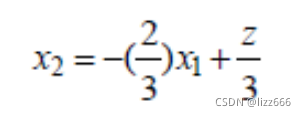

 浙公网安备 33010602011771号
浙公网安备 33010602011771号