Datawhale组队学习_Task04：详读西瓜书+南瓜书第5章

第5章 神经网络

5.1 神经元模型

• 基本定义：神经网络是由具有适应性的简单单元组成的广泛并行互联的网络，它的组织能够模拟生物神经系统对真实世界物体所做出的交互反应。
• M-P神经元模型：
  
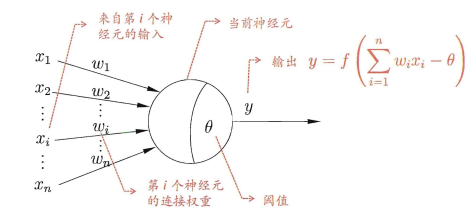
    在此模型中，神经元接收到来自其他n个神经元传递过来的带有权重的信号，并将总输入值与神经元的阈值进行比较，处理后以产生神经元的输出。
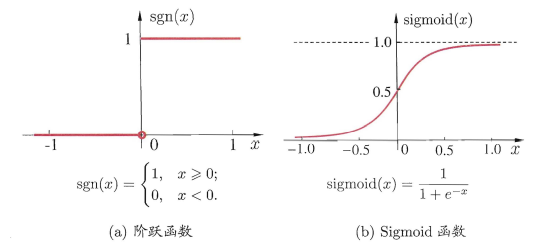
    通常使用挤压函数来作为激活函数，即如下图：
  

5.2 感知机与多层网络

• 感知机：两层神经元（输入层+输出层）组成，期中输入层接受外界输入信号后传递给输出层，输出层是M-P神经元，亦称“阈值逻辑单元”。
  
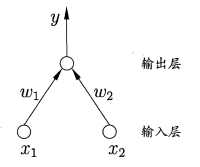
• 感知机的逻辑运算：
    假设对于阶跃函数y=\({f(\sum_{i}w_ix_i-\Theta)}\)
  • “与”（\({x_1\bigwedge x_2}\))：令\({w_1=w_2=1,\Theta=2}\)，则y=\({f(1·x_1+1·x_2-2)}\)，仅在\({x_1=x_2=1}\)时，y=1;
  • “或”（\({x_1\bigvee x_2}\))：令\({w_1=w_2=1,\Theta=0.5}\)，则y=\({f(1·x_1+1·x_2-0.5)}\)，仅在\({x_1=1或x_2=1}\)时，y=1;
  • “非”（\({\neg x_1}\))：令\({w_1=-0.6,w_2=0,\Theta=-0.5}\)，则y=\({f(-0.6·x_1+0·x_2+0.5)}\)，当\({x_1=1}\)时，y=0;当\({x_1=0}\)时，y=1;
• 对于一般常见神经网络的缺陷：
    由于感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元，其学习能力较为有限。若学习两类模式时线性可分的，则一定存在一个线性超平面将二者分开；否则若感知机在学习过程中发生振荡，无法求合适解。
    处理非线性可分问题时，通常考虑使用多层功能神经元。
    多层前馈神经网络：每层神经元与下一层神经元全互连，神经元之间不存在同层连接，也不存在跨层连接。

5.3 误差逆传播算法

• BP算法的主要工作流程：先将输入样例提供给输入层神经元，然后逐层将信号前传，知道产生输出层的结果；然后计算输出层的误差，再将误差逆向传播至隐层神经元，最后根据隐层神经元的误差来对连接权和与之进行调整，循环整个迭代过程，直到某些条件停止。
• BP算法的目标是要最小化训练集D上的积累误差
  伪代码如下所示：

#输入：训练集D={(${x_k,y_k}^m_{k=1}$)};
      #学习率${\eta}$
过程：
1.在（0，1）范围内随机初始化网络中所有连接权和阈值
2.repeat
3.  for all(x_k,y_k)∈D do
4.     根据当前参数计算当前样本的输出${\hat y_k}$;
5.     计算出输出层神经元的梯度项g_j;
6.     计算出隐层神经元的梯度项e_h;
7.     更新连接权与阈值；
8.   end for
9. until 达到停止条件
#输出：连接权与阈值确定的多层前馈神经网络

具体的公式推导内容在纸上，由于符号太多不想敲上来了，这里贴一个参照的博客 [神经网络值反向传播算法公式推导]（https://www.cnblogs.com/jsfantasy/p/12177275.html）