字符串 【上】
\(\mathcal{KMP}\)
\(next\) 数组的定义: \(next[i]\) 表示 \(str[1-i]\) 的前后缀的最大公共部分。应该比较好理解。
考虑 \(next\) 数组的构造方法。
先提到一件精巧灵活的事情:将字符串 \(str\) 自己和自己匹配,然后求出 \(next\) 数组。
由于是要求前后缀的最长公共部分,所以要用这个字符串的 \(prev\) 和 \(suff\) 相互匹配。
显然 \(next\) 数组是需要递推求得的,在已经知道 \(next[n-1]\) 的情况下求解 \(next[n].\)
先用 \(i\) 表示扫描到的 \(prev\) 的位置,然后再用 \(j\) 表示 \(suff\) 的位置。设有一个阴影部分 \(w\) ,\(w\) 表示现在的 \(next\) 结果形式化的映射到 \(S\) ,也就是交集的那个鬼畜集合。那么现在的 \(next\) 的值也就是 \(|w|.\) 关于求 \(w\) 的过程 \(\cdots\)
分类讨论如下:
\(1^\circ\) 当 \(S[i]=S[j]\) 时,必定会有一个 \(w'=w+s[i]\) ,\(next[i]=|w'|\)。显然。
\(2^\circ\) 当 \(S[i]\not = S[j]\) 时,考虑将 \(j\) 进行跳跃跳跃到一个最大的可以使 \(S[1,j] = S[n-j+1,n]\) 完全相同的位置。这里因为要调到一个最大的公共前后缀,所以转移 \(j=next[j]\) ,大概就是 \(next[next[i-1]]\) ,然后一直跳跳到了一个 \(S[i]=S[j]\) ,如果跳到最后都一直没有一个 \(j\) 可以满足 \(S[i]=S[j]\),那么就会有 \(next[i]=0.\)
用这个思路需要考虑到 \(next[1]=0.\)
然后转移到 \(next[n]\) 就大功告成了。
这个东西跳来跳去的好像不是很 \(O(n)\) 的样子啊。
这样分析:
\(j\) 每次回退都至少会回退 \(1\) 个单位,然后 \(j\) 一共前进是前进了 \(n\) 次,故而就有一个 \(n+n\) 然后合并同类项忽略常数之后得到的 \(O(n)\) 的低复杂度算法。常数不小。
$\text{code}$
// Qx 's data
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e6+10;
char a[N],b[N];
int nxt[N];
int n,m,ans;
inline void BuildNxt(void){
n=strlen(a+1),m=strlen(b+1);
int j=0;
for(int i=2;i<=m;++i){
while(j>0&&b[i]!=b[j+1])
j=nxt[j];
if(b[j+1]==b[i])++j;
nxt[i]=j;
}
return void();
}
inline void Kmp(void){
int j=0;
for(int i=1;i<=n;++i){
while(j>0&&b[j+1]!=a[i]) j=nxt[j];
if(b[j+1]==a[i]) ++j;
if(j==m) {printf("%d\n",i-m+1);j=nxt[j];}
}
}
int main(){
scanf("%s%s",a+1,b+1);
BuildNxt(),Kmp();
for(int i=1;i<=m;++i)
printf("%d ",nxt[i]);
}
现在已经知道 \(NEXT\) 数组了,剩下的就交给优化的暴力了。
\(\mathcal{MANACHER}\)
问题:求解一个串 \(S\) 中的各个位置为中心点的回文最大长度。
也就是一种求解最长回文串的算法。
首先考虑暴力:之前学长提到过一种方法:从每一个中心 \(i\) 开始延展,延展到一个最大的 \(r[i]\) 且 \(\forall a[i-j]=a[i+j] (0 \leq j \leq r[i])\)
这个时候这个延展的半径 \(r[i]\) 也就是这个位置的回文最大长度,\(ans[i] = 2\times r[i] -1.\) 原因显然。
然后考虑优化。注意到当一个串是回文的,当且仅当中心点的两边的字符串完全相同。所以当你求出一个回文串的左边部分,那么右边部分做法显然。设现在回文串的重心为 \(center\) , \(limit=center+r[center]\)
那么就有 \(r[i]=r[2center-i] (center \leq i\leq limit)\) 也就是对称过来的答案了。但是这不完全正确。
注意到这个串 \(ababzab\) 这个就不见得正确了。为什么呢?当 \(z\) 为中心的时候左边的 \(a\) 可以和更右边的 \(b\) 继续回文。
所以上面的式子答案就应为 \(r[i]=\min\{r[2center-i] (center \leq i\leq limit),i-limit\}\)
这个是对的,但是只能计算奇数情况下的回文,所以要把这个串扩展成这样的形式 \(:\)
这样子就可以直接操作了,\(ans[i]=r[i]-1\) 原因还是很显然,手动模拟一下就理解了。
复杂度证明:
最多暴力计算 \(n\) 次,然后最多通过公式计算 \(n\) 次,复杂度为 \(O(n).\)
$test{code}$
#include <bits/stdc++.h>
#define ll long long
using std::cin;
using std::cout;
const int N=2.2e7+10;
int r[N],a[N],b[N];
int center,limit,ans;
int n;
char ch[N];
int main(){
cin>>(ch+1);
n=strlen(ch+1);
for(int i=1;i<=n;++i)
b[i]=ch[i]+1;
for(int i=1;i<=n;++i)
a[2*i-1]=200,a[2*i]=b[i];
a[n<<1|1]=200;
for(int i=1;i<=(n<<1|1);++i){
if(i<=limit) r[i]=std::min(limit-i,r[2*center-i]);
while(i-r[i]>=1&&a[i-r[i]]==a[i+r[i]]) ++r[i];
if(i+r[i]>limit) center=i,limit=i+r[i];
ans=std::max(ans,r[i]-1);
}
cout<<\ans<<'\n';
}
例题
介绍几个鬼畜的例题:
-
\(P1723\) 就是模板的改装。
-
\(P4987\) 回文项链,直接不扩充就可以计算奇数情况了,然后断环成链就好。
-
\(CF1326D2\) 两边一定取,能取多少取多少,中间马拉车。
-
\(P4555\) 这个的话用 \(set\) 维护一下每个点能够 \(i+r[i]\) 达到的最小 \(i\) ,支持删除插入就好了。好像可以单调队列优化到 \(O(n).\) 还有一种我看不懂的动态规划方法。
-
\(CF17E\) 有多少对互不相交的回文串。
考虑设立两个数组 \(f\) , \(g\)
\(f[i]\) 表示以 \(i\) 开头的回文串数量, \(g[i]\) 表示以 \(i\) 结尾的回文串数量。
那么答案就是回文串总对数 \(-\) 相交回文串数量。而后者显然有
前者用回文串总数 \(Cnt\) 来做一个握手模型就好了。\(g\) 的 \(\sum\) 用前缀和累积就好了
那么 \(f,g\) 怎么求解呢?
用 \(f\) 举例子。
设现在找到了一个回文串中心 \(i,\) 而回文串最大半径为 \(r[i]\),则 \([i-r[i],i]\) 所有的地方都可以有一个以 \(j\) 开头的回文串,这个差分求解,毕竟只是最后询问一次,就很天使。
\(\mathcal{AC\quad MACHINE}\)
这是一种比较高科技的算法。基于 \(\mathcal{KMP}\) 的思想,然后就可以去搞事情。
首先建立一个对于模式串的字典树。再定义一个 \(fail\) 指针,其中 \(fail[i]\) 表示 \(0\rightarrow i\) 的路径所组成的字符串在字典树上的最长后缀位置,相当的不好理解.
然后考虑求出 \(fail[]\) ,转移。
\(\mathcal{SUF\quad ARRAY}\)
后缀数组,这个不好调试的。
首先约定:
-
\(rk[i]\) 表示字符串 \([i,n]\) 这个后缀的排名,是字典序排序之后的。
-
\(sa[i]\) 表示第 \(i\) 小的后缀的编号。
显然,\(rk[sa[i]]=sa[rk[i]]=i.\)
然后难点在于怎么求 \(rk,sa.\)
考虑到暴力算法:
将每一个字符串丢进一个池子 \(Lake.\) 然后 \(lake\) 里面排序求解,复杂度是 \(O(n^2 log_2 n)\) 的,因为比较字符串大小要 \(O(n)\) 的时间复杂度。
然后介绍一种优秀的倍增算法:
倍增求解后缀数组
约定:
我们将从 \(i\) 开始的后缀记作 \(T_i\)
考虑排序倍增的优秀复杂度为 \(O(n log_2 ^2 n)\)
那么倍增是很复杂的。
我们这样子考虑:
首先求出所有长度为 \(1\) 的字符串的 \(sa\) 和 \(rk\) .
也就是 \(sa_1, rk_1\) 显然这是可以通过排序得到的。这就告诉我们我们已经求得了第一层的 \(rk.\)
然后根据这个再转移到第二层去。进行下一轮的排序。排序按照 \(rk[i] ,rk[i+1]\) 的关键字顺序排序,显然,这可以得到第二层的 \(rk_2\)
然后再转移到第三层。同理,用 \(rk[i], rk[i+2]\) 排序,得到 \(rk_4\)
然后不断地转移。以此类推,通过 \(rk[i], rk[i+w]\) 排序,然后得到各种各样的鬼畜玩意,其中当 \(w\geq n\) 的时候 \(rk_w\) 即为所求。
排序的时候是求 \(sa\) 数组,然后怕不是就结束了。
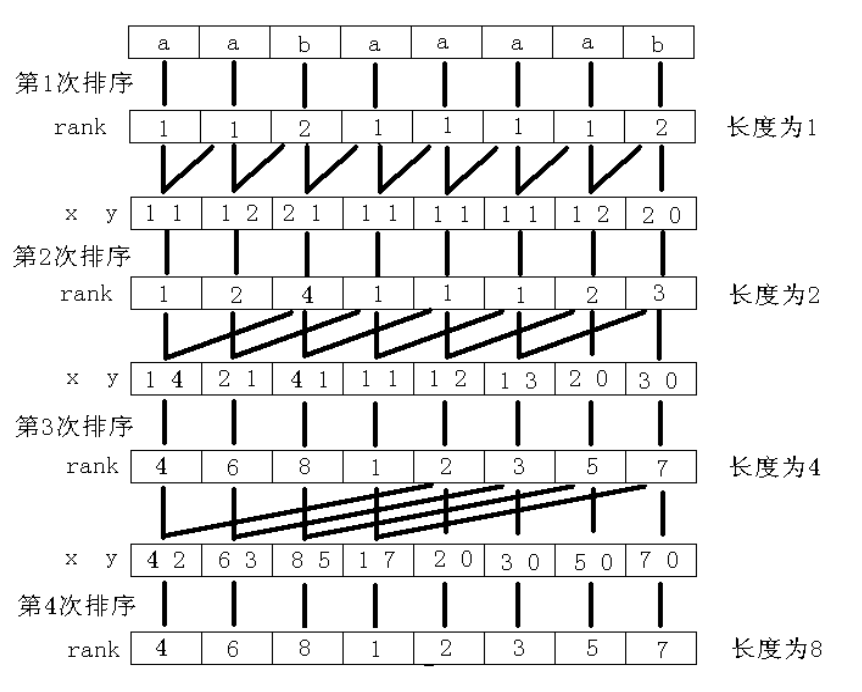
上图是后缀数组 \(oi-wiki\) 上面的图片。
$\text{code}$
#include <bits/stdc++.h>
#define ll long long
#define oldrk rk0
using std::cin;
using std::cout;
using std::cerr;
const int N=1e6+10;
char str[N<<1];
int rk[N<<2],rk0[N<<2],sa[N<<2];
char ch[N<<1];
int n,w,cnt;
int main(){
scanf("%s",ch+1);
n=strlen(ch+1);
for(int i=1;i<=n;++i)
sa[i]=i,rk[i]=ch[i];
for(w=1;w<n;w<<=1){
std::sort(sa+1,sa+n+1,[](int x,int y){
return rk[x]==rk[y]?rk[x+w]<rk[y+w]:rk[x]<rk[y];
});
memcpy(rk0,rk,sizeof(rk));
int i;
for(cnt=0,i=1;i<=n;++i){
if(rk0[sa[i]]==rk0[sa[i-1]] &&
rk0[sa[i]+w]==rk0[sa[i-1]+w]){
rk[sa[i]]=cnt;
}else{
rk[sa[i]]=++cnt;
}
}
}
for(int i=1;i<=n;++i)
printf("%d ",sa[i]);
return 0;
}
实测模板 \(10^6\) 可以 \(ac.\) 最大数据点 \(1.18s\) 非常的不错。\(c++20 O2\)
\(lcp \& SA\)
还要提出一个新的东西,它就是 \(lcp.\)
我们这样约定约定:
\(lcp(str1,str2)\) 是两个字符串的最长相同的前缀。
而 \(lcp(x,y)\) 是 \(lcp(sa[x],sa[y]).\)
还有一个比较憨憨的定理 : \(lcp(str1,str3)=\min\{lcp(str1,str2),lcp(str2,str3)\},j\leq i\leq k\) 原因十分显然。
定义 \(h\) 数组: \(h[i]=lcp(i,i-1)\)
而我们可以知道这件事情之后我们就可以很快地求出两个子串的 \(lcp,\) 也就是 \(\min_k \{h[i]\}.\) 原因也比较显然。
这个 \(\min\) 可以被 \(st\) 表或者 \(segt\) 维护。
还有几个比较重要的用法:
不同子串的数量
提出一个思想:一个串中的子串一定是串的某一个后缀的前缀。
再来,问题可以被转化为所有串的数量减去本质相同的串的数量的差。也就是 \(\dfrac{n(n+1)}{2}\) 减去相同的串的数量。
而根据 \(h\) 数组的定义,又可以知道 \(h[i]\) 就是 \(i,i-1\) 的 \(lcp\) 长度,有多长就有多少个子串相等,也就是 \(i\) 对答案的贡献。
所以答案即
代码不算长到离谱。
$\text{code}$
#include <bits/stdc++.h>
#define ll long long
using std::cin;
using std::cout;
using std::cerr;
const int N=1e6+10;
char ch[N];
int rk[N],rk0[N],sa[N];
int ht[N];
int n,w;
inline void _sa(void){
for(int i=1;i<=n;++i)
sa[i]=i,rk[i]=ch[i];
for(w=1;w<n;w<<=1){
std::sort(sa+1,sa+n+1,[](int x,int y){
return rk[x]==rk[y]?rk[x+w]<rk[y+w]:rk[x]<rk[y];
});
int cnt=0;
memcpy(rk0,rk,sizeof rk);
for(int i=1;i<=n;++i)
if(rk0[sa[i]]==rk0[sa[i-1]] &&
rk0[sa[i]+w]==rk0[sa[i-1]+w])
rk[sa[i]]=cnt;
else rk[sa[i]]=++cnt;
}
}
inline void _geth(void){
int k=0;
for(int i=1;i<=n;++i) rk[sa[i]] =i;
for(int i=1;i<=n;++i){
if(k) --k;
while(ch[i+k]==ch[sa[rk[i]-1]+k]) ++k;
ht[rk[i]]=k;
}
}
signed main(){
scanf("%d",&n);
scanf("%s",ch+1);
_sa();
_geth();
ll ans=1ll*n*(n+1)/2;
for(int i=1;i<=n;++i)
ans-=ht[i];
printf("%lld\n",ans);
return 0;
}
例题:
可以发现后缀数组的题经常要和各种各样的算法结合起来。那么先来两道裸后缀数组。
\(\color{white}{P4248 [AHOI2013] 差异}\)
给定一个长度为 \(n\) 的字符串 \(S\),令 \(T_i\) 表示它从第 \(i\) 个字符开始的后缀。求
其中,\(\text{len}(a)\) 表示字符串 \(a\) 的长度,\(\text{lcp}(a,b)\) 表示字符串 \(a\) 和字符串 \(b\) 的最长公共前缀。
我们可以考虑将问题转化一下:
左边的是一个常数,\(d=\dfrac{(n-1)n(n+1)}{2}\)
右边可以用 \(h\) 数组进行化简。
单调栈维护维护就好了。代码不是很好写但是思路清楚其实并不复杂。最后发现是我的 \(h\) 数组求错了,笑。
$\text{code}$
#include <bits/stdc++.h>
#define int long long
#define ll long long
using std::cin;
using std::cout;
using std::cerr;
const int N=5e5+10;
char ch[N];
int rk[N],rk0[N],sa[N];
int ht[N];
int n,w;
inline void _sa(void){
for(int i=1;i<=n;++i)
sa[i]=i,rk[i]=ch[i];
for(w=1;w<n;w<<=1){
std::stable_sort(sa+1,sa+n+1,[](int x,int y){
return rk[x]==rk[y]?rk[x+w]<rk[y+w]:rk[x]<rk[y];
});
int cnt=0;
memcpy(rk0,rk,sizeof rk);
for(int i=1;i<=n;++i)
if(rk0[sa[i]]==rk0[sa[i-1]] &&
rk0[sa[i]+w]==rk0[sa[i-1]+w])
rk[sa[i]]=cnt;
else
rk[sa[i]]=++cnt;
}
}
inline void _h(void){
int k=0;
for(int i=1;i<=n;++i)
rk[sa[i]]=i;
for(int i=1;i<=n;++i){
if(k) --k;
while(ch[i+k]==ch[sa[rk[i]-1]+k]) ++k;
ht[rk[i]]=k;
}
}
inline void input(void){
scanf("%s",ch+1);
n=strlen(ch+1);
}
std::stack<int> st;
int lim;
ll ans;
inline void debug(void){
for(int i=1;i<=n;++i)
printf("rk[i]=%d ",rk[i]);
puts("");
}
int l[N],r[N];
inline void work(void){
ans=(n+1)*(n-1)*n/2;
while(!st.empty()) st.pop();
st.push(1);
for(int i=2;i<=n;++i){
while(!st.empty() && ht[st.top()]>ht[i])
r[st.top()]=i,st.pop();
if(st.empty()) lim=0;
else lim=st.top();
l[i]=lim;
st.push(i);
}
while(!st.empty()) r[st.top()]=n+1,st.pop();
for(int i=2;i<=n;++i){
ans-=2ll*(r[i]-i)*(i-l[i])*ht[i];
}
return printf("%lld\n",ans),void();
}
signed main(){ input(),_sa(),_h(),work(); }
其实主要难度在于推式子。
\(\color{white}{P3181 找出相同字符}\)
注意到这道题一共有两个字符串,考虑对字符串进行合并操作。合并的方法参见 \(manacher\) ,将两个字符串之间添加一个字符 # ,然后原式可化为重复串的方案数,稍加容斥之后就可以求得答案了。
然后考虑求 \(\operatorname{Ans} s\) 的值。
那么一个串有多少重复的串呢?
根据上面 \(\operatorname{lcp(i,j)}\) 定理
好家伙,这个式子又变成了一个全部区间的最小值之和问题。单调栈维护。
$\text{code}$
// Qx 's data
#include <bits/stdc++.h>
#define ll long long
using std::cin;
using std::cout;
using std::cerr;
#define db double
const int N=5e5+10;
int rk[N],rk0[N],sa[N],ht[N],l[N],r[N],stack[N];
int w,top;
inline ll calc(char *ch,int n){
memset(l,0,sizeof l);
memset(rk,0,sizeof rk);
memset(r,0,sizeof r);
memset(sa,0,sizeof sa);
memset(rk0,0,sizeof rk0);
memset(ht,0,sizeof ht);
top=w=0;
for(int i=1;i<=n;++i)
rk[i]=ch[i],sa[i]=i;
for(w=1;w<=n;w<<=1){
std::stable_sort(sa+1,sa+n+1,[](int x,int y){
return rk[x]==rk[y]?rk[x+w]<rk[y+w]:rk[x]<rk[y];
});
memcpy(rk0,rk,sizeof rk);
int cnt=0;
for(int i=1;i<=n;++i){
if(rk0[sa[i]]==rk0[sa[i-1]] &&
rk0[sa[i]+w]==rk0[sa[i-1]+w])
rk[sa[i]]=cnt;
else
rk[sa[i]]=++cnt;
}
}
int k=0;
for(int i=1;i<=n;++i)
rk[sa[i]]=i;
for(int i=1;i<=n;++i){
if(k) --k;
while(ch[i+k]==ch[sa[rk[i]-1]+k])++k;
ht[rk[i]]=k;
}
stack[++top]=1;
for(int i=2;i<=n;++i){
while(top&&ht[stack[top]]>=ht[i]) r[stack[top]]=i,--top;
l[i]=stack[top];
stack[++top]=i;
}
while(top) r[stack[top--]]=n+1;
ll ret=0;
for(int i=2;i<=n;++i)
ret+=(i-l[i])*(r[i]-i)*ht[i];
return ret;
}
int len1,len2,len3;
char s1[N],s2[N],s3[N];
int main(){
scanf("%s %s",s1+1,s2+1);
len1=strlen(s1+1),len2=strlen(s2+1);
len3=len1+len2+1;
memcpy(s3,s1,sizeof s1);
s3[len1+1]='#';
for(int i=1;i<=len2;++i)
s3[i+len1+1]=s2[i];
return printf("%lld\n",-calc(s1,len1)-calc(s2,len2)+calc(s3,len3)),0;
}
\(\color{white}{P5546 最长公共子串}\)
把字符串拼起来,也就是用 # 连接,然后在上面做最长重复且属于所有串的后缀均出现过的子串。也就是满足以下条件的子串
-
重复过
-
其中包含的后缀可以覆盖所有的串
这样的子串是合格的。要求求得一个最长的串满足上述条件。
最长也就是要求最大化 \(\min\{h[k]\} _{i < k \leq j}\) 而且要使第二个条件满足。
上面式子是单调不升的,所以最小化 \(j-i\) ,显然这是可以通过 two-pointer 维护的,而 2. 条件可以用类似莫队或者用前缀和维护,至于查询 \(\min\) ,滑动窗口、线段树、st 均可。这里选用线段树。因为很好写。
然后直接算就行了。
复杂度看似十分玄学,实际上瓶颈还是在于前面求 \(h\) 数组的 \(\mathcal{O(nlog^2n)}\),写出来就可以 \(ac.\) 主要要注意上面的 \(<\) 符号,很容易被阴。
$\text{code}$
// Qx 's data
#include <bits/stdc++.h>
#define ll long long
using std::cin;
using std::cout;
using std::cerr;
const int N=20005,Time=10,inf=0x3f3f3f3f;
int T,n,w;
char ch[N*5];
int ed[Time+5];
int rk[N*10],sa[N*10],rk0[N*10];
int h[N*5];
char s[10][N];
int col[N*10],vis[N*10];
inline int gf(int x){
return vis[x];
}
inline void _sa(void){
for(int i=1;i<=n;++i)
rk[i]=ch[i],sa[i]=i;
for(w=1;w<=n;w<<=1){
std::stable_sort(sa+1,sa+n+1,[](int x,int y){
return rk[x]==rk[y]?rk[x+w]<rk[y+w]:rk[x]<rk[y];
});
int cnt=0;
memcpy(rk0,rk,sizeof rk);
for(int i=1;i<=n;++i){
if(rk0[sa[i]]==rk0[sa[i-1]] &&
rk0[sa[i]+w]==rk0[sa[i-1]+w])
rk[sa[i]]=cnt;
else
rk[sa[i]]=++cnt;
}
}
}
inline void _h(void){
int k=0;
for(int i=1;i<=n;++i)
rk[sa[i]]=i;
for(int i=1;i<=n;++i){
if(k) --k;
int j=sa[rk[i]-1];
while(ch[i+k]==ch[j+k] && ch[i+k]!='#') ++k;
h[rk[i]]=k;
}
return;
}
#define ls (rt<<1)
#define rs (rt<<1|1)
#define mid ((l+r)>>1)
#define lson ls,l,mid
#define rson rs,mid+1,r
struct segtree{
int tree[N*40];
inline void pushup(int rt,int l=0,int r=0){
return tree[rt]=std::min(tree[ls],tree[rs]),void();
}
int query(int rt,int l,int r,int L,int R){
if(L<=l && r<=R) return tree[rt];
int res=inf;
if(L<=mid) res=std::min(res,query(lson,L,R));
if(R> mid) res=std::min(res,query(rson,L,R));
return res;
}
void Build(int rt,int l,int r){
if(l==r) return tree[rt]=h[l],void();
Build(lson) , Build(rson);
return pushup(rt,l,r),void();
}
}G;
int l=0,r=0,cs=0,ans=-inf;
inline void add(int x){
if(!x) return;
++col[x];
if(col[x]==1) ++cs;
}
inline void del(int x){
if(!x) return;
--col[x];
if(col[x]==0) --cs;
}
inline void buildvis(void){
for(int i=1;i<=T;++i){
for(int j=ed[i-1]+1;j<ed[i];++j)
vis[rk[j]]=i;
}
}
inline void two_pointer(void){
_sa(),_h();
G.Build(1,1,n);
buildvis();
l=r=1;
add(gf(1));
while(r<=n){
if(cs==T){
while(cs==T)del(gf(l)),++l;
--l,add(gf(l));
ans=std::max(ans,G.query(1,1,n,l+1,r));
}
++r;
add(gf(r));
}
printf("%d\n",ans);
}
int main(){
cin>>T;
for(int i=1;i<=T;++i) cin>>(s[i]+1);
for(int i=1;i<=T;++i) ed[i]=ed[i-1]+strlen(s[i]+1)+1;
for(int i=1;i<=T;++i){
int len=strlen(s[i]+1);
for(int j=1;j<=len;++j)
ch[++n]=s[i][j];
ch[++n]='#';
}
--n;
two_pointer();
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号