欧几里得算法

首先介绍一下欧几里得算法，又称作辗转相除法，用于求两个自然数的最大公约数

这是目前已知的求最大公约数的最快算法

 

引理：gcd(m,n)=gcd(n,m mod n)//这就是辗转相除法的核心,假设m是大于n的

注：gcd(a,b)是a和b的最大公约数，mod是模运算

 

分析一下？

我们假设k是m n的公约数，m=xn+y

因为k整除m，k整除n，k整除xn，所以k一定整除y

所以可得出上式gcd(m,n)=gcd(n,m mod n)

我们知道，任何数和0的最大公约数是它本身

以此类推可以求出，当n等于0的时候，此时的m就是最大公约数

 

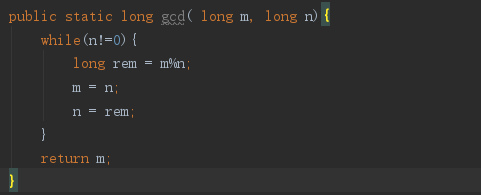
代码

 

 

时间复杂度分析

在m mod n的过程中，最坏的结果是产生的y在m/2附近，此时n也接近m/2，下次的m变成了n

在最坏的情况下值减少一半，所以时间复杂度是O（logn）的

(但我们可以看出两次最坏情况并不可能相继发生，所以实际的时间复杂度会更低