DS博客作业04--图
0.PTA得分截图

1.本周学习总结
1.1 总结图内容
图分类
1:有向图
图解:
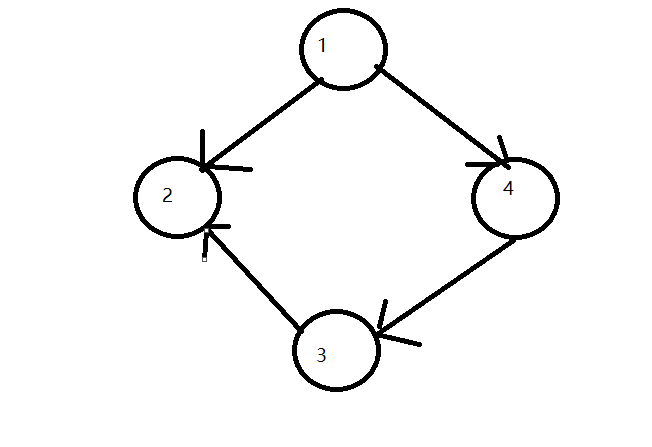
特征;
- 有向图称由顶点集和弧集构成的图。“弧”是有方向的边,用尖括号表示。
- 若存在一条边(i,j),则称顶点i和顶点j互为邻接点。
- 每两个顶点之间都存在着一条边,称为完全无向图, 包含有n(n-1)/2条边。
- 若从顶点i到顶点j有路径,则称顶点i和j是连通的。若图中任意两个顶点都连通称为连通图,否则称为非连通图。无向图G中的极大连通子图称为连通分量。
2:无向图
图解:

特征: - 没有方向边。边用圆括号表示。
- 存在一条边<i,j>,则称此边是顶点i的一条出边,同时也是顶点j的一条入边;称顶点i 和顶点j 互为邻接点。
- 每两个顶点之间都存在着方向相反的两条边,称为完全有向图,包含有n(n-1)条边。
- 若任意两个顶点之间都存在一条有向路径,则称此有向图为强连通图。 否则,其各个强连通子图称作它的强连通分量。
3:带权图:
图解:

特征 - 图中每一条边都可以附有一个对应的数值,这种与边相关的数值称为权。
- 边上带有权的图称为带权图,也称作网。
图存储结构
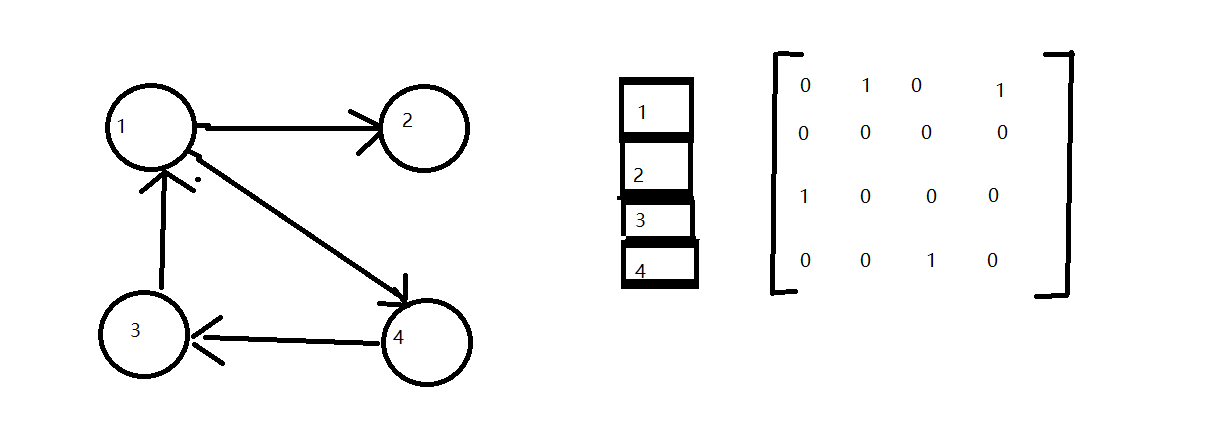
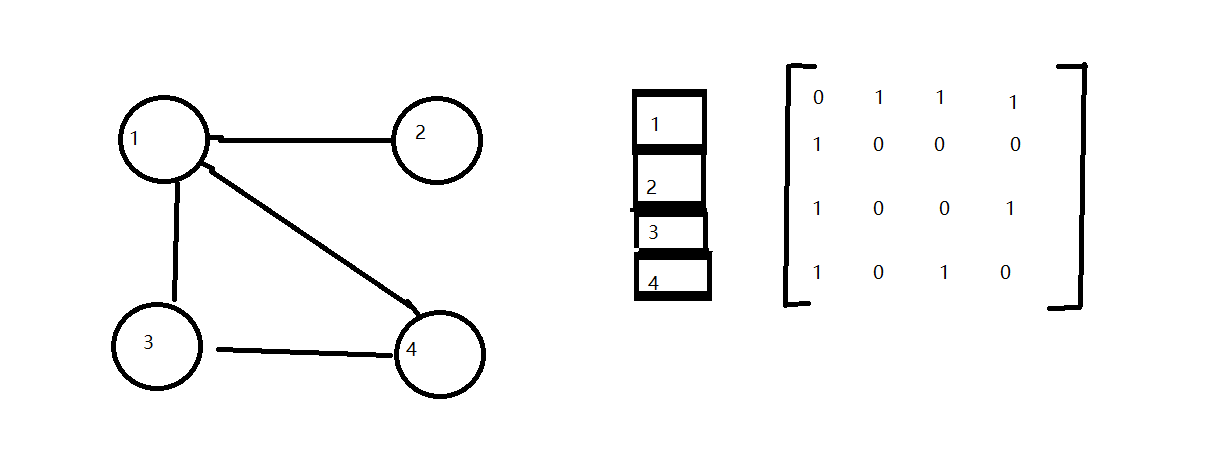
1:邻接矩阵
举例:
- 有向图
- 无向图
- 带权图

结构体定义
typedef struct //图的定义
{ int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,边数
VertexType vexs[MAXV]; //存放顶点信息
} MatGraph;
MatGraph g;//声明邻接矩阵存储的图
建图
void CreateMGraph(MGraph &g, int n, int e)
{
int i, j;
g.n = n;
g.e = e;
int a, b;
for (i = 1;i <= n;i++)
{
for (j = 1;j <= n;j++)
{
g.edges[i][j] = 0;//初始化
}
}
for (i = 0;i < e;i++)
{
cin >> a >> b;
g.edges[a][b] = g.edges[b][a] = 1;//非带权图
}
}
- 时间复杂度O(n^2)
- 用于记录较多数量的图,当容易造成空间浪费
2:邻接表
举例:
有向图
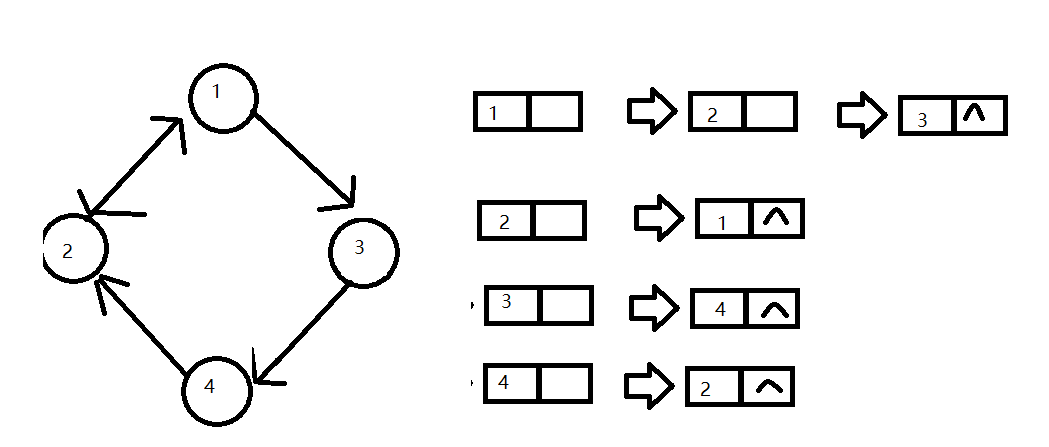
无向图
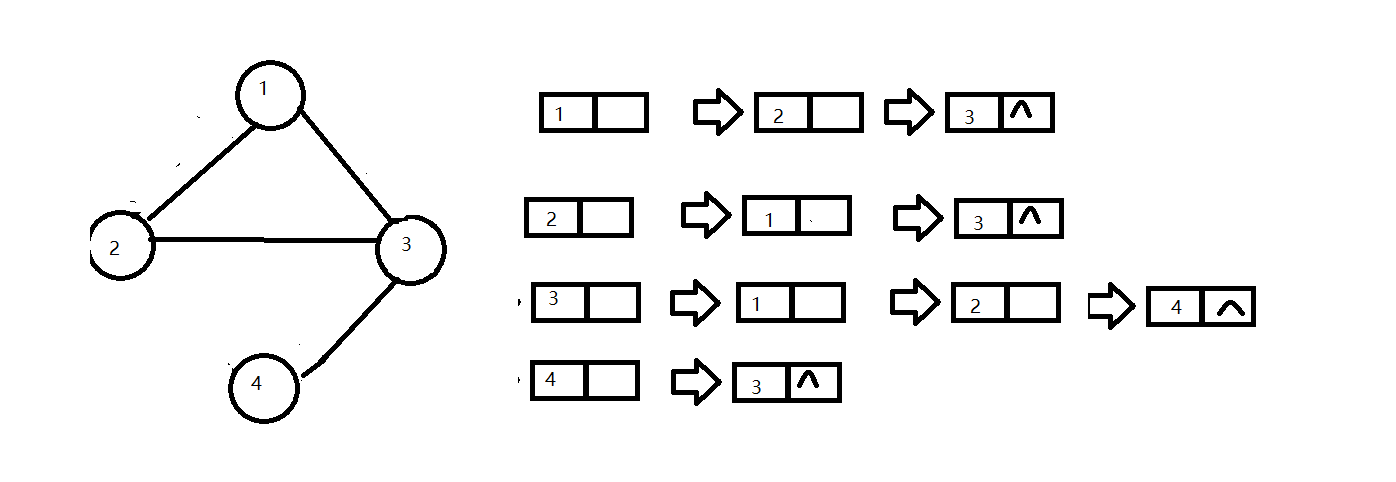
带权图
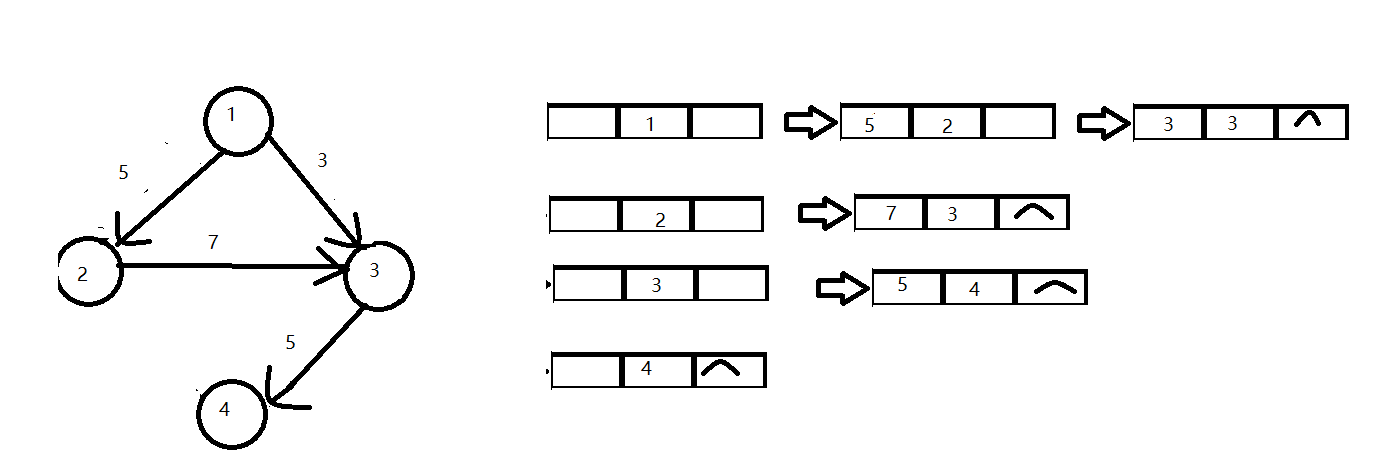
结构体定义:
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode;
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
InfoType info; //该边的权值等信息
} ArcNode;
typedef struct
{ VNode adjlist[MAXV] ; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
AdjGraph *G;//声明一个邻接表存储的图G
建图:
void CreateAdj(AdjGraph *&G, int n, int e) //创建图邻接表
{
int i, j, a, b;
ArcNode *p;
G = new AdjGraph;
for (i = 1;i < n;i++)
{
G->adjlist[i].data = i;
G->adjlist[i].firstarc = NULL;
}
for (i = 1;i <= e;i++)
{
cin >> a >> b;
ArcNode *p = new ArcNode;
p->adjvex = b;
p->nextarc = G->adjlist[a].firstarc;
G->adjlist[a].firstarc = p;
/*p = new ArcNode;
p->adjvex = a;
p->nextarc = G->adjlist[b].firstarc;
G->adjlist[b].firstarc = p;//无向图
}
}
- 时间复杂度:O(n+e);
- 节省空间,缺难查看两边之间是否有边。
图遍历
1.深度遍历
方法:
- 从图中某个初始顶点v出发,首先访问初始顶点v。
- 选择一个与顶点v相邻且没被访问过的顶点w为初始顶点,再从w出发进行深度优先搜索,直到图中与当前顶点v邻接的所有顶点都被访问过为止。
遍历代码:
遍历邻接矩阵
void DFS(MGraph g, int v)//深度遍历
{
visited[v] = 1;
if (!flag)
{
flag = 1;
cout << v;
}
else cout << " " << v;
for (int i = 1;i <= g.n;i++)
{
if (g.edges[v][i] == 1 && (!visited[i]))
DFS(g, i);
}
}
遍历邻接表
void DFS(AdjGraph *G, int v)//v节点开始深度遍历
{
ArcNode *p;
visited[v] = 1; //置已访问标记
if(!flag)
{
cout<<v;
flag=1;
}
else cout<<" "<<v;
p = G->adjlist[v].firstarc;
while (p != NULL)
{
if (visited[p->adjvex] == 0) DFS(G, p->adjvex);
p = p->nextarc;
}
}
2.广度遍历
方法:
- 访问初始点v,接着访问v的所有未被访问过的邻接点。
- 按照次序访问每一个顶点的所有未被访问过的邻接点。
- 依次类推,直到图中所有顶点都被访问过为止。
遍历邻接矩阵:
void BFS(MGraph g, int v)//广度遍历
{
int num, front, rear;
int Q[MAXV];
front = rear = -1;
cout << v;
visited[v] = 1;
Q[++rear] = v;
while (front != rear)
{
v = Q[++front];
for (int i = 1;i <= g.n;i++)
{
if (g.edges[v][i] == 1 && (!visited[i]))
{
cout << " " << i;
visited[i] = 1;
Q[++rear] = i;
}
}
}
}
遍历邻接表:
void BFS(AdjGraph *G, int v) //v节点开始广度遍历
{
ArcNode *p;
queue<int>qu;
visited[v] = 1;
cout << v;
qu.push(v);
while (!qu.empty())
{
v = qu.front();
qu.pop();
p = G->adjlist[v].firstarc;
while (p != NULL)
{
if (visited[p->adjvex] == 0)
{
cout << " " << p->adjvex;
visited[p->adjvex] = 1;
qu.push(p->adjvex);
}
p = p->nextarc;
}
}
}
3:判断是否连通图
方法:
- visited数组记录通过某节点遍历的所有节点,存在节点未被遍历则非连通图
代码:
int visited[MAXV];
bool Connect(AdjGraph *G) //判断无向图G的连通性
{ int i;
bool flag=true;
for (i=0;i<G->n;i++) //visited数组置初值
visited[i]=0;
DFS(G,0);
for (i=0;i<G->n;i++)
if (visited[i]==0)
{ flag=false;
break;
}
return flag;
}
4:寻找图路径
方法:
- 采用深度优先遍历的方法。
- 增加path[i],存放路径。
- 递归函数添加形参d,表示目前递归深度。path[d]=图结点
- 当从顶点u遍历到顶点v后,输出path并返回。
代码:
void FindaPath(AGraph *G,int u,int v,int path[],int d)
{ //d表示path中的路径长度,初始为-1
int w,i; ArcNode *p;
visited[u]=1;
d++; path[d]=u; //路径长度d增1,顶点u加入到路径中
if (u==v) //找到一条路径后输出并返回
{ printf("路径为:");
for (i=0;i<=d;i++) printf("%d ",path[i]);
printf("\n");
return; //找到一条路径后返回
}
p=G->adjlist[u].firstarc; //p指向顶点u的第一个相邻点
while (p!=NULL)
{ w=p->adjvex; //相邻点的编号为w
if (visited[w]==0)
FindaPath(G,w,v,path,d);
p=p->nextarc; //p指向顶点u的下一个相邻点
}
}
5:寻找最短路径(无权重)
方法:
- 采用广度遍历保证最先发现的路径为最短路径
- 利用parent记录前驱
- 输出时逆向,利用parent关系输出
代码:
typedef struct
{
int data; //顶点编号
int parent; //前一个顶点的位置
} QUERE; //非环形队列类型
void ShortPath(ALGraph *G,int u,int v)
{
//输出从顶点u到顶点v的最短逆路径
ArcNode *p;
int w,i;
QUERE qu[MAXV]; //非环形队列
int front=-1,rear=-1; //队列的头、尾指针
int visited[MAXV];
for (i=0; i<G->n; i++) //访问标记置初值0
visited[i]=0;
rear++; //顶点u进队
qu[rear].data=u;
qu[rear].parent=-1;
visited[u]=1;
while (front!=rear) //队不空循环
{
front++; //出队顶点w
w=qu[front].data;
if (w==v) //找到v时输出路径之逆并退出
{
i=front; //通过队列输出逆路径
while (qu[i].parent!=-1)
{
printf("%2d ",qu[i].data);
i=qu[i].parent;
}
printf("%2d\n",qu[i].data);
break;
}
p=G->adjlist[w].firstarc; //找w的第一个邻接点
while (p!=NULL)
{
if (visited[p->adjvex]==0)
{
visited[p->adjvex]=1;
rear++; //将w的未访问过的邻接点进队
qu[rear].data=p->adjvex;
qu[rear].parent=front;
}
p=p->nextarc; //找w的下一个邻接点
}
}
}
最小生成树
- 概率:
1.一个连通图的生成树是一个极小连通子图,它含有图中全部n个顶点和构成一棵树的(n-1)条边。不能回路。
2.由深度优先遍历得到的生成树称为深度优先生成树。由广度优先遍历得到的生成树称为广度优先生成树。
3.对于带权连通图G ,n个顶点,n-1条边。根据深度遍历或广度遍历生成生成树,树不唯一。其中权值之和最小的生成树称为图的最小生成树。
4.非连通图:需多次调用遍历过程。每个连通分量中的顶点集和遍历时走过的边一起构成一棵生成树。所有连通分量的生成树组成非连通图的生成森林。 - 方法:
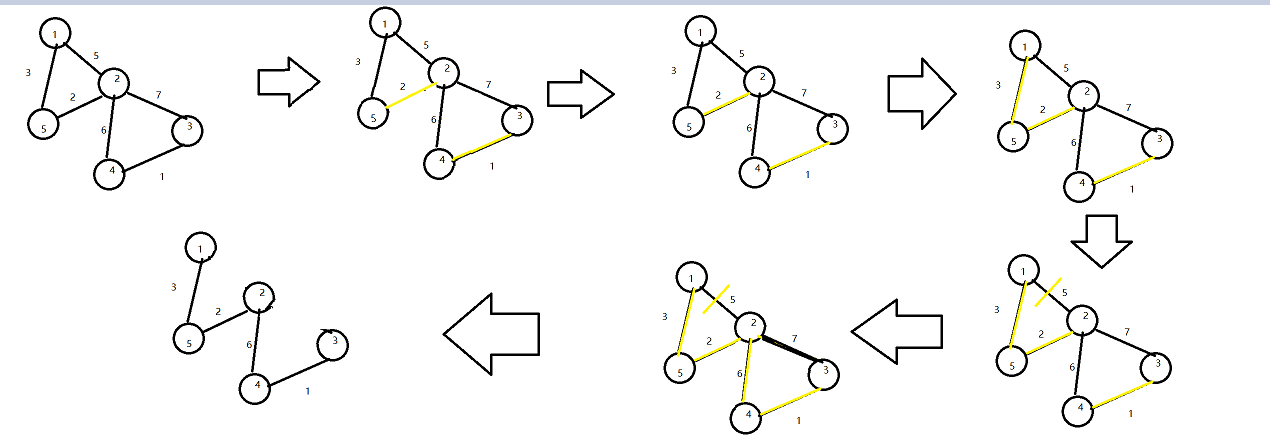
1.普里姆算法(Prim)
过程: - 初始化U={v}。v到其他顶点的所有边为候选边;
- 从候选边中挑选权值最小的边输出,设该边在V-U中的顶点是k,将k加入U中;
- 考察当前V-U中的所有顶点j,修改候选边:若(j,k)的权值小于原来和顶点k关联的候选边,则用(k,j)取代后者作为候选边。
- 重复后两个步骤骤n-1次,使得其他n-1个顶点被加入到U中。
图解:

代码:
#define INF 0x3f3f3f
void Prim(MGraph g,int v)
{
int lowcost[MAXV],min,closest[MAXV],i,j,k;
for(i=0;i<g.n;i++)
{
lowcost[i]=g.edges[v][i];
closest[i]=v;
}
for(i=1;i<g.n;i++) //找出n-1个顶点
{
min=inf;
for(j=0;j<g.n;j++) //在V-U中找出离U最近的顶点k
{
if(lowcost[j]!=0&&lowcost[j]<min)
{
min=lowcost[j]; //k记录最近顶点编号
k=j;
}
}
lowcost[k]=0; //标记k已经加入U
for(j=0;j<g.n;j++) //修正
{
if(lowcost[j]!=0&&g.edges[k][j]<lowcost[j])
{
lowcost[j]=g.edges[k][j];
closest[j]=k;
}
}
}
}
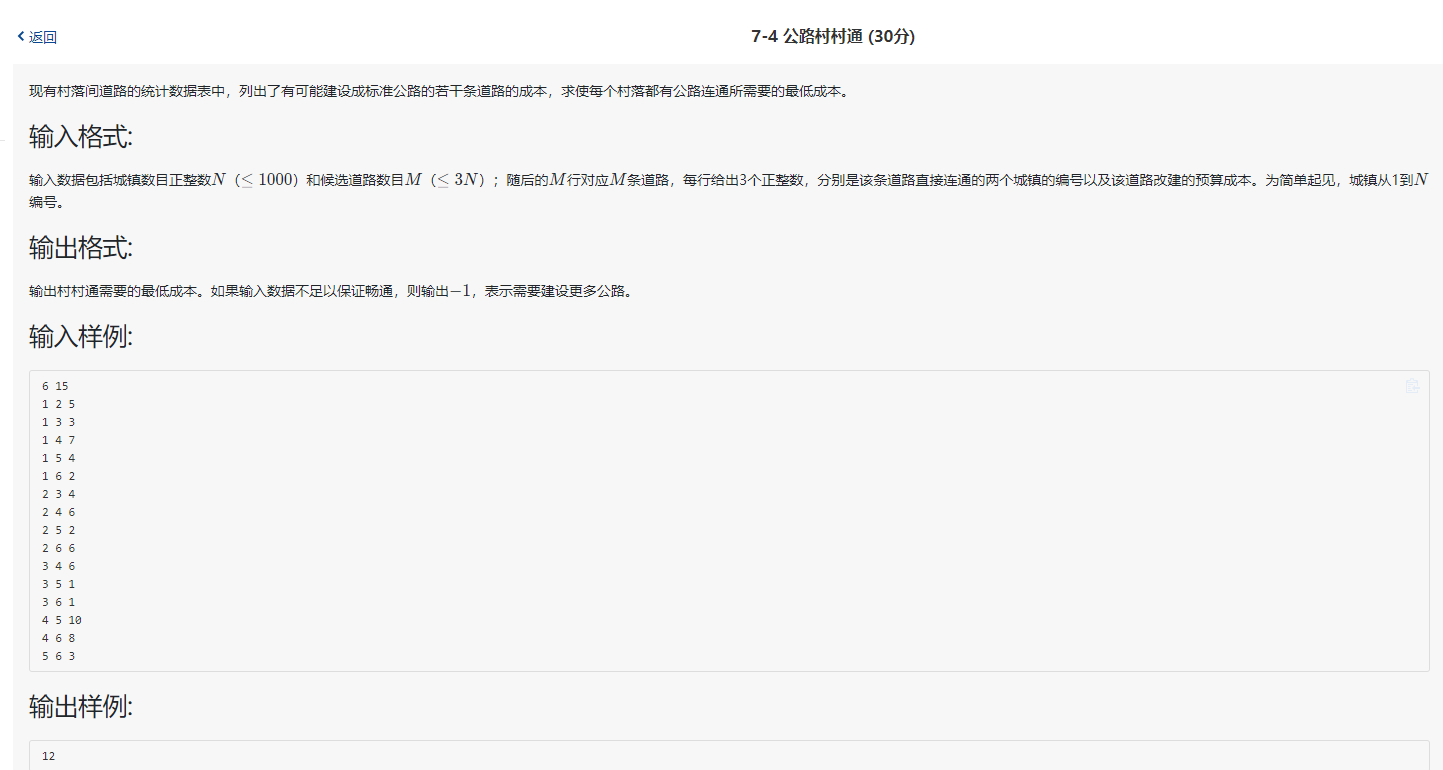
2.克鲁斯卡尔算法(kruskal)
过程:
- 置U的初值等于V(即包含有G中的全部顶点),TE的初值为空集(即图T中每一个顶点都构成一个连通分量)。
- 将图G中的边按权值从小到大的顺序依次选取: 若选取的边未使生成树T形成回路,则加入TE;否则舍弃,直到TE中包含(n-1)条边为止。
图解:
存储结构:
typedef struct
{ int u; //边的起始顶点
int v; //边的终止顶点
int w; //边的权值
} Edge;
Edge E[MAXV];
代码:
void Kruskal(AdjGraph *g)
{ int i,j,u1,v1,sn1,sn2,k;
int vset[MAXV]; //集合辅助数组
Edge E[MaxSize]; //存放所有边
k=0; //E数组的下标从0开始计
for (i=0;i<g.n;i++) //由g产生的边集E,邻接表
{ p=g->adjlist[i].firstarc;
while(p!=NULL)
{ E[k].u=i;E[k].v=p->adjvex;
E[k].w=p->weight;
k++; p=p->nextarc;
}
}
Sort(E,g.e); //用快排对E数组按权值递增排序
for (i=0;i<g.n;i++) //初始化集合
vset[i]=i;
k=1; //k表示当前构造生成树的第几条边,初值为1
j=0; //E中边的下标,初值为0
while (k<g.n) //生成的顶点数小于n时循环
{
u1=E[j].u;v1=E[j].v; //取一条边的头尾顶点
sn1=Find(u1,vset);
sn2=Find(v1,vset); //分别得到两个顶点所属的集合编号
if (sn1!=sn2) //两顶点属于不同的集合
{ printf(" (%d,%d):%d\n",u1,v1,E[j].w);
k++; //生成边数增1
vset[sn1]=sn2;
}
j++; //扫描下一条边
}
}
int Find(int v,int vest[])
{
if(vset[v]==v)
return v;
else
return Find(vset[v],vset)
}
应用:
伪代码:
用边存储结构读取数据
初始化vset数组使各数的起始节点设为本身
while k记录已保存的边数目!=顶点数-1
寻找权值最小的边
if 该边的权值为极大值
图不连通 输出-1并退出循环
寻找这边始末节点的起始节点
if 起始节点不相等
将其中一边的起始节点的起始节点记录为另一边的起始节点
记录权值
将该边的权值设为极大值
if 记录的边数=顶点数-1
输出权值的和
代码:
#define MAXV 3003
#define INF 1000000
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
using namespace std;
//图的邻接矩阵
int find(int i, int vset[]);
typedef struct //图的定义
{
int **edges; //邻接矩阵
int n, e; //顶点数,弧数
} MGraph; //图的邻接矩阵表示类型
typedef struct
{
int u;
int v;
int w;
}Edge[MAXV];
int main()
{
int vset[MAXV];
int i;
Edge p;
MGraph g;
int a, b, c;
cin >> g.n >> g.e;
for ( i = 1; i <= g.e; i++)
{
cin >> p[i].u >> p[i].v >> p[i].w;
}
int min;
for ( i = 1; i <= g.n; i++)
{
vset[i] = i;
}
int k = 1;
int ans = 0;
int j = 0;
int sn1, sn2;
while (k!=g.n)
{
min = INF;
for ( i = 1; i <= g.e; i++)
{
if (p[i].w<min)
{
min = p[i].w;
j = i;
}
}
if (p[j].w==INF)
{
cout << -1;
break;
}
sn1 = find(p[j].u,vset);
sn2 = find(p[j].v,vset);
if (sn1!=sn2)
{
vset[sn2] = sn1;
ans = ans + p[j].w;
k++;
}
p[j].w = INF;
}
if (k==g.n)
{
cout << ans;
}
}
int find(int i,int vset[])
{
if (vset[i]==i)
{
return i;
}
else
{
return find(vset[i],vset);
}
}
最短路径
1.狄克斯特拉(Dijkstra)算法
过程:
- S={入选顶点集合,初值V0},T={未选顶点集合}。
- 若存在<V0,Vi>,距离值为<V0,Vi>弧上的权值
- 若不存在<V0,Vi>,距离值为∞
- 从T中选取一个其距离值为最小的顶点W, 加入S
- S中加入顶点w后,对T中顶点的距离值进行修改:重复上述步骤1,直到S中包含所有顶点,即S=V为止。
- 重复上述步骤1,直到S中包含所有顶点,即S=V为止。
图解:

代码:
void Dijkstra(MatGraph g,int v)
{ int dist[MAXV],path[MAXV];
int s[MAXV];
int mindis,i,j,u;
for (i=0;i<g.n;i++)
{ dist[i]=g.edges[v][i]; //距离初始化
s[i]=0; //s[]置空
if (g.edges[v][i]<INF) //路径初始化
path[i]=v; //顶点v到i有边时
else
path[i]=-1; //顶点v到i没边时
}
s[v]=1; //源点v放入S中
for (i=0;i<g.n;i++) //循环n-1次
{ mindis=INF;
for (j=0;j<g.n;j++)
if (s[j]==0 && dist[j]<mindis)
{ u=j;
mindis=dist[j];
}
s[u]=1; //顶点u加入S中
for (j=0;j<g.n;j++) //修改不在s中的顶点的距离
if (s[j]==0)
if (g.edges[u][j]<INF &&dist[u]+g.edges[u][j]<dist[j])
{ dist[j]=dist[u]+g.edges[u][j];
path[j]=u;
}
}
Dispath(dist,path,s,g.n,v); //输出最短路径
}
2.应用
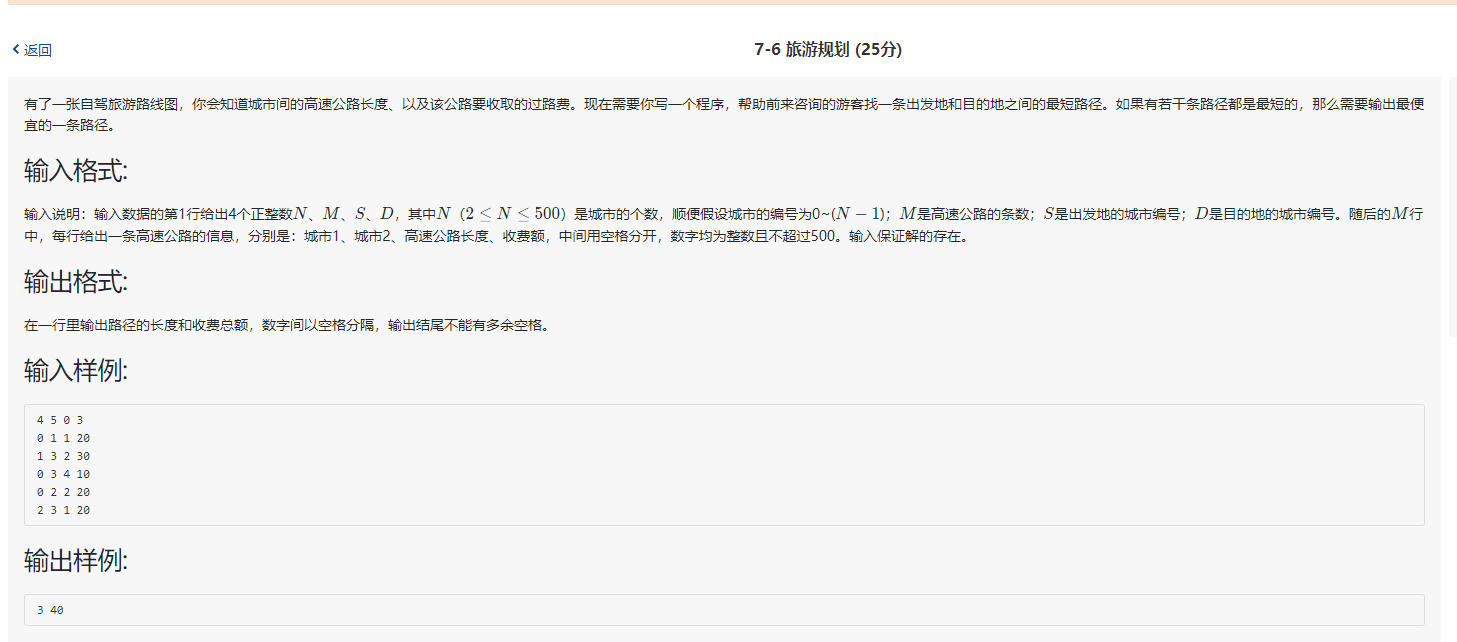
伪代码:
typedef struct
{
int edges[MAXV][MAXV];//距离
int cost[MAXV][MAXV];//花费
int n, e;
}MGraph;
用图结构记录数据
vset数组记录节点
记录起始节点vset数组为1
记录dist数组为起始节点到其他节点的距离
记录cost数组为起始节点到其他节点的路费
for i =0 to 节点数
if 该节点在vset数组未被记录且该节点小于min1(记录当前最短路径)
min1=原点到该节点路径
min2=远点到该节点路费
记录该节点
将该节点记录vset数组
for i=0 同节点数
if 记录的节点到某节点距离加该节点到起始节点的距离小于起始节点到某节点距离
更新起始节点到某节点的最短距离为前者
更新起始节点到某节点的路费为前者的路费和
else if 两者的距离相等且前者的路费小于后者的路费
更新起始节点到某节点路费为前者的路费和
代码
#include<iostream>
using namespace std;
#define MAXV 501
#define INF 100000
typedef struct
{
int edges[MAXV][MAXV];//距离
int cost[MAXV][MAXV];//花费
int n, e;
}MGraph;
int D;
void Dijkstra(MGraph g, int v);
int main()
{
MGraph g;
int N, M, S;
int i;
int a, b, c, d;
cin >> N >> M >> S >> D;
g.n = N;
g.e = M;
for (int i = 0; i < N; i++)//初始化距离
{
for (int j = 0; j < N; j++)
{
g.edges[i][j] = INF;
}
}
for ( i = 0; i < g.e; i++)
{
int a, b, c, d;
cin >> a >> b >> c >> d;
g.edges[a][b] = c;
g.edges[b][a] = c;
g.cost[a][b] = d;
g.cost[b][a] = d;
}
Dijkstra(g, S);
}
void Dijkstra(MGraph g, int v)
{
int s[MAXV];//记录访问过
int dist[MAXV];//距离第一顶点距离
int costs[MAXV];//花费
int min1, min2;
int k;//记录最小路径的下标
for (int i = 0; i < g.n; i++)
{
s[i] = 0;
dist[i] = g.edges[v][i];
costs[i] = g.cost[v][i];
}
s[v] = 1;
int i, t;
for ( i = 0; i < g.n; i++)
{
min1 = INF;
min2 = INF;
for (int j = 0; j < g.n; j++)
{
if (!s[j] && dist[j] < min1)
{
min1 = dist[j];
min2 = costs[j];
k = j;
}
}
s[k] = 1;
for ( t = 0; t < g.n; t++)
{
if (!s[t] && min1 + g.edges[k][t] < dist[t])
{
dist[t] = min1 + g.edges[k][t];
costs[t] = min2 + g.cost[k][t];
}
else if (!s[t] && min1 + g.edges[k][t] == dist[t] && min2 + g.cost[k][t] < costs[t])
costs[t] = min2 + g.cost[k][t];
}
}
cout << dist[D] << " " << costs[D];
}
拓扑排序
过程:
- 从有向图中选取一个没有前驱的顶点,并输出之
- 从有向图中删除此顶点以及所有以他为尾的弧
- 重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止
图解:
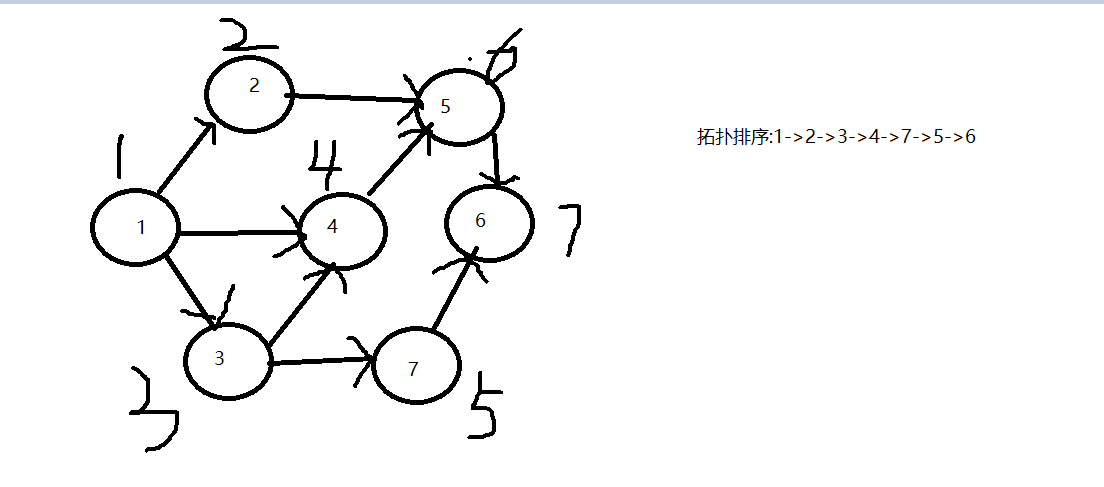
储存结构:
typedef struct //表头节点类型
{ vertex data; //顶点信息
int count; //存放顶点入度
ArcNode *firstarc; //指向第一条弧
} VNode;
代码:
void TopSort(AdjGraph *G)
{
int number[MAXV];
int a[MAXV];
int flag = 0;
int top = -1;
ArcNode *p;
int i;
for (i = 0; i < G->n; i++)
{
G->adjlist[i].count = 0;
}
for ( i = 0; i < G->n; i++)
{
p = G->adjlist[i].firstarc;
while (p!=NULL)
{
G->adjlist[p->adjvex].count++;
p = p->nextarc;
}
}
for ( i = 0; i < G->n; i++)
{
if (G->adjlist[i].count==0)
{
number[++top] = i;
}
}
while (top>-1)
{
i = number[top--];
a[flag++] = i;
p = G->adjlist[i].firstarc;
while (p!=NULL)
{
G->adjlist[p->adjvex].count--;
if (G->adjlist[p->adjvex].count==0)
{
number[++top] = p->adjvex;
}
p = p->nextarc;
}
}
if (flag!=G->n)
{
cout << "error!";
return;
}
for ( i = 0; i < G->n; i++)
{
if (i!=G->n-1)
{
cout << a[i] << ' ';
}
else
{
cout << a[i];
}
}
}
关键路径
方法:
- 用顶点表示事件,用有向边e表示活动,边的权表示活动持续的时间,是带权的有向无环图
- 关键路径:从有向图的源点到汇点的最长路径
- 关键活动:关键路径中的边
- 源点:入度为0
- 汇点:出度为0
- 事件的最早开始时间:事件v的最早开始事件,一定是所有前驱事件x,y,z完成,才轮到事件v
- ve(v)=max{ve(x)+a,ve(y)+b,ve(z)+c}(从左往右)
- 事件的最迟开始时间:要保证后继所有事件能按时完成,取最小
- vl(v)=min{vl(x)-a,vl(y)-b,vl(z)-c}(从右往左)
图解:
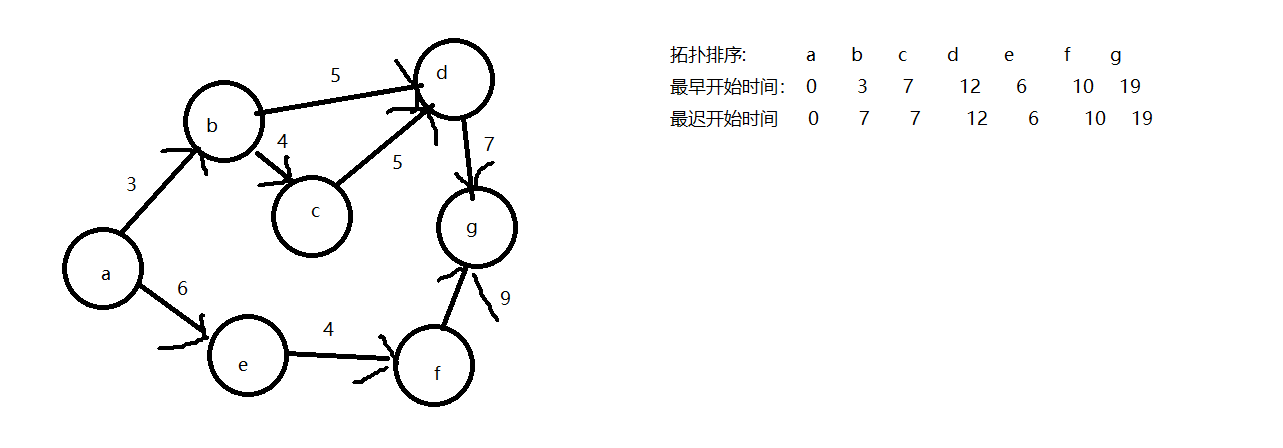
1.2谈谈你对图的认识与看法
图的学习大部分是帮助我们对某些算法的运用,让我们在面对复杂的流程时能根据算法一步步得找出最优解,这章的代码练习感觉较难,每一道题都有关于图所需要的独特的见解。对图的进一步学习,使我不仅仅在递归函数的理解上逐渐加深,对结构体的多重用法也有了十足的长进。
2.阅读代码
2.1题目及解题代码
题目:
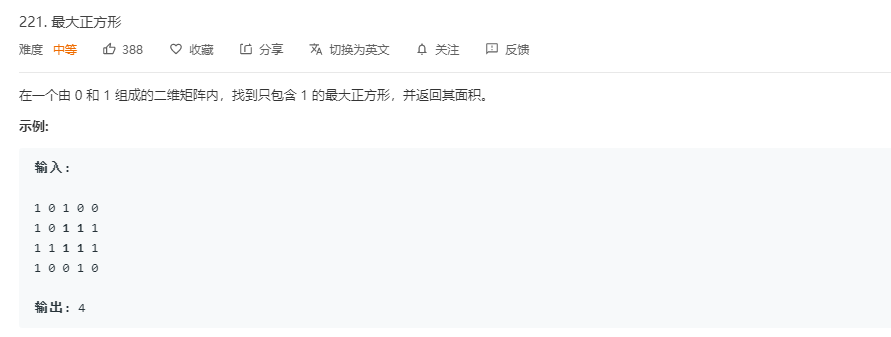
代码:
class Solution {
public int maximalSquare(char[][] matrix) {
int maxSide = 0;
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return maxSide;
}
int rows = matrix.length, columns = matrix[0].length;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
if (matrix[i][j] == '1') {
// 遇到一个 1 作为正方形的左上角
maxSide = Math.max(maxSide, 1);
// 计算可能的最大正方形边长
int currentMaxSide = Math.min(rows - i, columns - j);
for (int k = 1; k < currentMaxSide; k++) {
// 判断新增的一行一列是否均为 1
boolean flag = true;
if (matrix[i + k][j + k] == '0') {
break;
}
for (int m = 0; m < k; m++) {
if (matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0') {
flag = false;
break;
}
}
if (flag) {
maxSide = Math.max(maxSide, k + 1);
} else {
break;
}
}
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
}
2.1.1 该题的设计思路
设计思路:设正方形的最大边长为0,遍历邻接矩阵,当出现1时,先比较最大边长与1的大小,大的设为最大边长,之后遍历出现1位置向右与向下一行所有的数是否都为一,如果都为1,记录该点的边长为1+k(k为遍历的行数),并判断1+k与最大边长大小,大的修正为最大边长,无都为1则退出循环继续遍历邻接矩阵直到找到另一个1或者遍历完全。遍历完成后输出最大边长的平方为面积大小。
时间复杂度:O(mnmin(m,n) ^2)
空间复杂度:O(1)
2.1.2 该题的伪代码
用邻接表矩阵记录图数据
遍历邻接矩阵
if 邻接矩阵某值为1
记录该位置为[i][j]
for k =1 to 矩阵边长
if a[i+k][j+k]==0
该图边长不满足1+k退出循环
for m=0 to m<k
if a[i+k][j+m]==0||a[i+m][j+k]==0
该图边长不满足1+k退出循环
记录最大边长与k+1的较大值为新的最大边长
输出最大长度的平方为面积
2.1.3运行结果
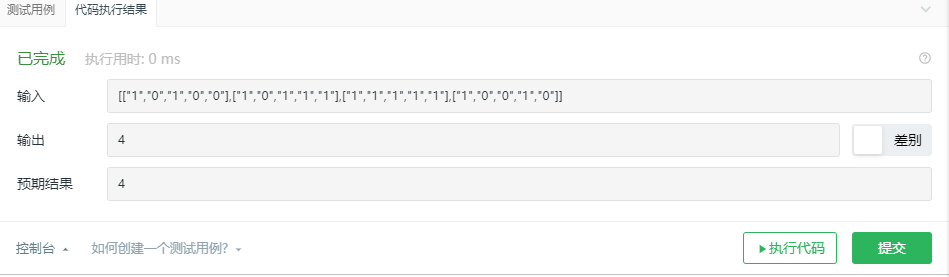
2.1.4分析该题目解题优势及难点。
该题的难点在于如何减少时间复杂度,为了确保该范围内的内容全为1,需要将预想的正方形完全遍历,且如何确保自己找到的正方形最大,需要完全遍历邻接矩阵。
该题的解题优势在于将面积转化为边长的形式,且对于一些小正方形的遍历不会过量重复遍历邻接矩阵,也根据情况判断出之前已遍历的1位置不会成为新的正方形的组成部分来减少遍历。通过记录最大边长也不需要担心面积的数字过大。
2.2 题目及解题代码
题目:
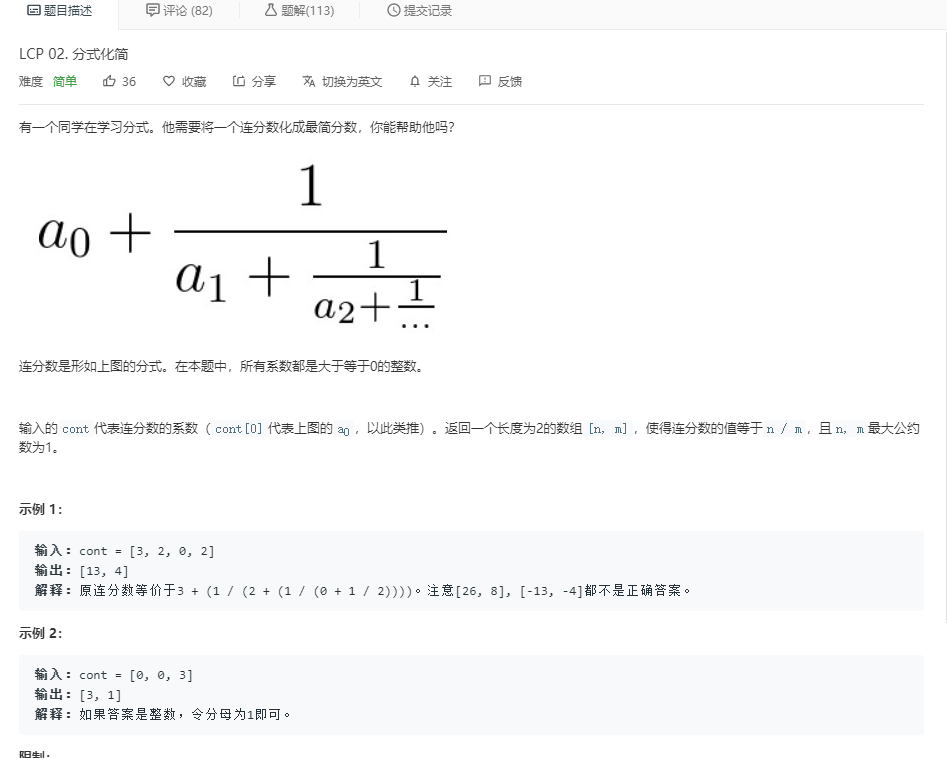
代码:
vector<int> fraction(vector<int>& cont)
{
int up = 1,down = cont[cont.size()-1];
for(int i = cont.size()-2;i >= 0;--i)
{
up += cont[i] * down;
swap(up,down);
}
return {down,up};
}
2.2.1 该题的解题思路
解题思路:记录数据至栈后,先将1作为分子,出栈的第一个数字作为分母,之后再出栈一个数字,将分子改为该数字乘以分母+原分子后,将该分子与分母调换位置,则变成1除以该生成数的结果,循环至数组结束,最终再将分子分母调换位置则得到正确答案
时间复杂度:O(n)
空间复杂度:O(n)
2.2.2伪代码
记录数据进栈
int 分子=1 分母=栈顶
出栈
while 栈不为空
分子=分子+分母*栈顶
出栈
分子分母调换位置
分子分母调换位置
输出分子分母
2.2.3运行结果

2.2.4分析该题目解题优势及难点。
该题的难点在于算法方式的思考,由于计算机不能直接记录分母,所有如果硬计算结果只能得到一堆小数,所以需要将分子与分母进行分开计算,但即使这样算法没推敲还是很难想到。
解题优势在通过从最后一个数字开始往回进行推导,不仅使整个代码看起来十分简单易懂,还很方便轻松地将问题解决,算法方面非常地取巧,将困难的算数变为简单的两数直接的加乘。
2.3题目及解题代码
题目:
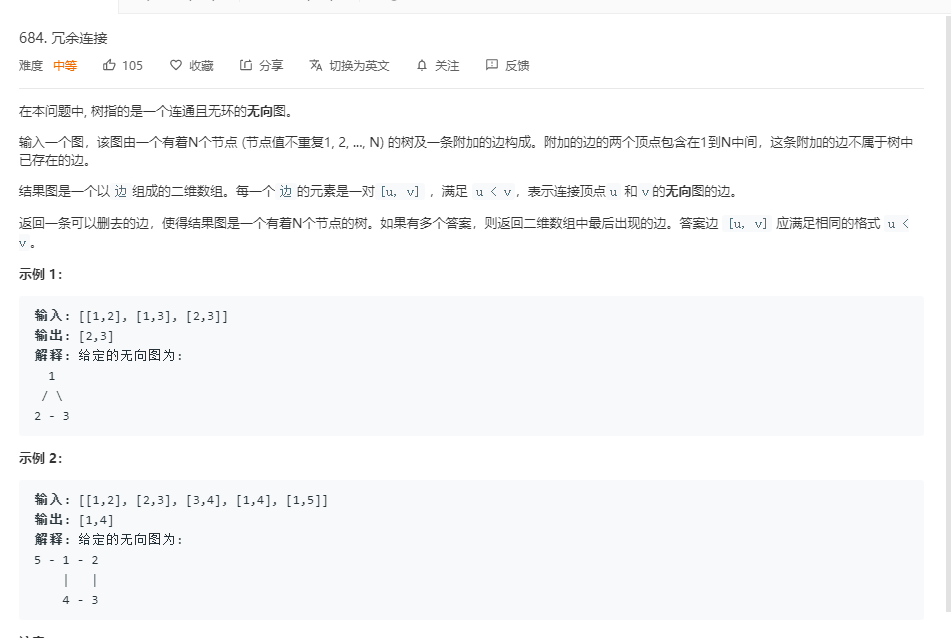
代码:
class Solution {
public int[] findRedundantConnection(int[][] edges) {
int numV = edges.length; //节点个数
int[] union = new int[numV+1];
for(int i = 0; i < union.length; i++)
union[i] = i;
for(int i = 0; i < edges.length; i++){
int s = edges[i][0];
int t = edges[i][1];
if(union[s] == union[t]){
int[] res = new int[]{s, t};
return res;
}
else{//合并两个分量
int sId = union[s];
for(int j = 0; j < union.length; j++){
if(union[j] == sId)
union[j] = union[t];
}
}
}
return null;
}
}
2.3.1该题的解题思路
解题思路:为保证这n个节点构成树,这需要保证这些节点不会拥有强连通部分使其节点都两两相连,便可以使用并查集来确认各节点的起始节点,连通的两点起始节点不相同则设为相同,相同则可以删除。
图解:

时间复杂度:O(N)
空间复杂度:O(N)
2.3.2该题的伪代码
用边储存结构储存图
设各点的起始节点为本身
for i=1 to 边数
查找边两点的起始节点
if 两节点起始节点相等
返回该边,退出循环
else for j=1 to 边数
寻找等于其中一节点的起始节点的所有点,将他们起始节点设为另一节点的起始节点
2.3.3运行结果
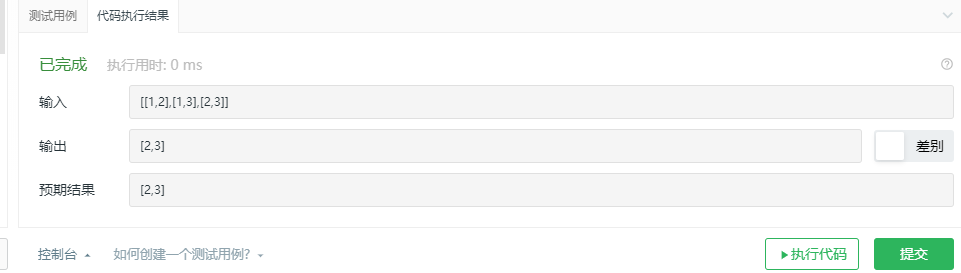
2.3.4分析该题目解题优势及难点
该题的难点在于如何根据将图变为树形式来引导至要判断该图的强连通部分以防止树的某节点与他的兄弟或不属于他的根节点相连,代码的思考与最少生成树判断该边是否可以符合收录条件相似,比较简单
该题的解题优势在于使用并查集收录根节点,而不是使用深度遍历判断某节点是否导致连通,减少了图的遍历与时间复杂度。




