DS博客作业03--树
0.PTA得分截图

1.本周学习总结
1.1 总结树及串内容
- 串:
1.串的知识点:
- 头文件:#include
- 构造函数
string str; //生成一个空字符串
string str ("ABC") //等价于 str="ABC"
string str ("ABC", n) // 将"ABC"存到str里,最多存储前n个字节
string s("ABC",a,b) //将"ABC"的a位置,做为字符串开头,存到str里.且最多存储b个字节.
string s(n, 'A') //存储n个'A'到str里
- 使用函数
str.length(); //获取字符串长度
str.size(); //获取字符串数量,等价于length()
str.swap(str2); //替换str1 和 str2 的字符串
str.puch_back ('A'); //在str1末尾添加一个'A'字符,参数必须是字符形式
str.append ("ABC"); //在str1末尾添加一个"ABC"字符串,参数必须是字符串形式
str.insert (2,"ABC"); //在str1的下标为2的位置,插入"ABC"
str.erase(2); //删除下标为2的位置,比如: "ABCD" --> "AB"
str.erase(2,1); //从下标为2的位置删除1个,比如: "ABCD" --> "ABD"
str.clear(); //删除所有
str.replace(2,4, "ABCD"); //从下标为2的位置,替换4个字节,为"ABCD"
str.empty(); //判断为空, 为空返回true
2.BF算法(暴力匹配法)
- 匹配方式:
从主串s1的pos位置出发,与子串s2第一位进行匹配
若相等,接着匹配后一位字符
若不相等,则返回到s1前一次匹配位置的后一位,接着与s2的起始位进行匹配
直到与s2全部匹配成功,则返回在s1中开始完全匹配的下标
图解:

- 具体代码
int BF(string s,string t)
{
int i=0,j=0;
while(i<s.length&&j<t.length)//两个串都没有扫描完
{
if(s.data[i]==t.data[j])
{
i++;j++
}
else
{
i=i-j+1;j=0;//扫描目标串的i回退,子串从头开始匹配
}
if(j>=t.length)
return i-t.length;
else
return -1;匹配失败,返回-1
}
}
3.KML算法
优势:KMP 算法永不回退 主串s 的指针 i,不走回头路(不会重复扫描 s),而是借助 dp 数组中储存的信息把子串t移到正确的位置继续匹配。
原理:
当T[i] != P[j]时
有T[i-j ~ i-1] == P[0 ~ j-1]
由P[0 ~ k-1] == P[j-k ~ j-1]
必然:T[i-k ~ i-1] == P[0 ~ k-1]
具体代码:
int KMP(SqString s, SqString t)
{
int nextval[MAX];
int i, j;
i = j = 0;
GetNextval(t, nextval);
while (i < s.len && j < t.len)
{
if (j == -1 || s.data[i] == t.data[j])
{
i++;
j++;
}
else
{
j = nextval[j];
}
}
if (j >= t.len) return (i - t.len);
else return (-1);
}
void GetNextval(SqString t, int nextval[])
{
int j = 0, k = -1;
nextval[0] = -1;
while (j < t.len)
{
if (k == -1 || t.data[j] == t.data[k])
{
j++;
k++;
if (t.data[j] != t.data[k])
{
nextval[j] = k;
}
else
{
nextval[j] = nextval[k];
}
}
else
{
k = nextval[k];
}
}
}
- 二叉树
1.储存结构:
typedef struct node *BTree;
typedef struct node
{
ElemType data;
struct node *lchild,*rchild;
//每一个左右指针,指向的都是一棵二叉树
}BTNode;
2.二叉树建法
- 先序遍历建法 如:abc##de#g##f###
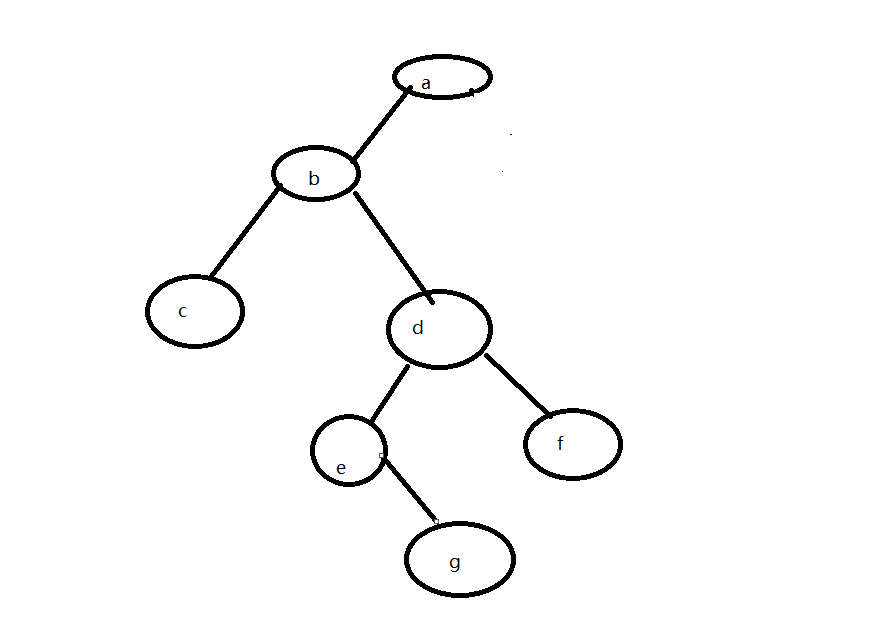
具体代码
BTree CreateBT(string str,int&i)
{
if(i>=len-1)
return NULL;
if(str[i]=='#')
return NULL;
BTree bt=new BTnode;
bt->data=str[i];
bt->lchild=CreateBT(str,++i);
bt->rchild=CreateBT(str,++i);
}
- 层次遍历建法,例如:#ABC#DEF##G#H##I //第一个#不算
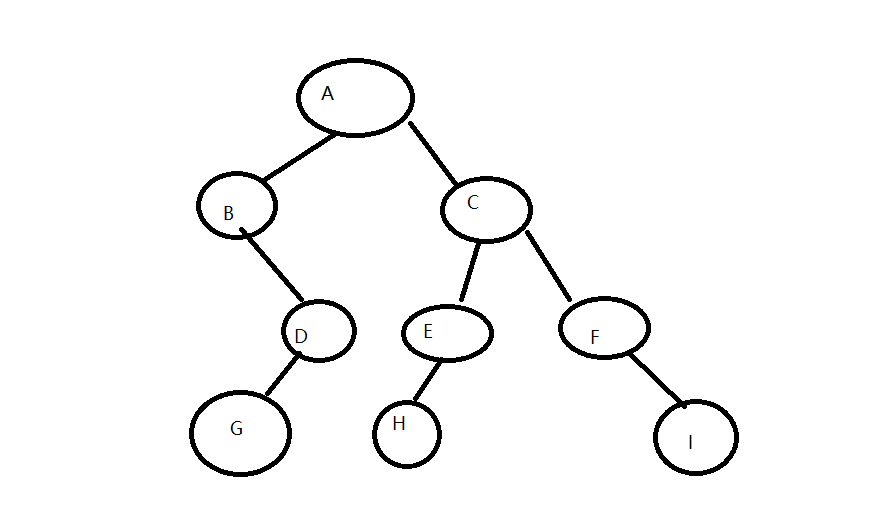
具体代码:
BTree CreateBTree(string str,int i)
{
int len;
BTree bt;
bt=new TNode;
len=str.size();
if(i>len-1||i<=0)
{
return NULL;
}
if(str[i]=='#')return NULL;
bt->data=str[i];
bt->lchild=CreateBTree(str,2*i);
bt->rchild=CreateBTree(str,2*i+1);
return bt;
}
3.二叉树的遍历
- 先序遍历:
void PreorderPrintLeaves(BinTree BT)
{
if (BT != NULL)
{
cout<<BT->Data<<" ";
PreorderPrintLeaves(BT->Left);
PreorderPrintLeaves(BT->Right);
}
}
- 中序遍历
void PreorderPrintLeaves(BinTree BT)
{
if (BT != NULL)
{
PreorderPrintLeaves(BT->Left);
cout<<BT->Data<<" ";
PreorderPrintLeaves(BT->Right);
}
}
- 后序遍历
void PreorderPrintLeaves(BinTree BT)
{
if (BT != NULL)
{
PreorderPrintLeaves(BT->Left);
PreorderPrintLeaves(BT->Right);
cout<<BT->Data<<" ";
}
}
4.二叉树的应用:
- 中序输出度为1的结点
具体代码:
void InorderPrintNodes(BiTree T)
{
if (T == NULL)
return;
else if (T != NULL)
{
InorderPrintNodes(T->lchild);
if ((T->lchild != NULL && T->rchild == NULL) || (T->lchild == NULL && T->rchild != NULL))
printf(" %c", T->data);
InorderPrintNodes(T->rchild);
}
}
- 树
1.储存结构
- 双亲储存结构:
typedef struct
{
int data;
int parent;//存放双亲的位置
}PTree[MaxSize];
图解:

- 孩子兄弟链储存结构:
typedef struct node
{
int data;
struct node*brother
struct node*son;
}BTnode;
图解:

2.树的应用
- 朋友圈
具体代码:
#include<iostream>
#define MAX 30005
using namespace std;
int pre[MAX];
int Num[MAX];
int Find(int a)
{
if (pre[a] == a)return a;/*寻找该个体归属的朋友圈 */
return pre[a] = Find(pre[a]);
}
void Judge(int a, int b)
{
int A = Find(a);
int B = Find(b);
if (A != B)/*判断两个体归属的朋友圈是否一致*/
{
pre[B] = A;
Num[A] = Num[B] + Num[A];/*叠加两个朋友圈的人数*/
}
}
int main()
{
int i = 0;
int M, N;
cin >> N >> M;
for ( i = 0; i <=N ; i++)
{
pre[i] = i;/*初始设定自身为独立的朋友圈*/
Num[i] = 1;/*初始设定朋友圈的人数*/
}
while (M--)
{
int number;
cin >> number;
int a, b;
if (number == 1)
cin >> a;
else
{
cin >> a;
while (--number)
{
cin >> b;
Judge(a, b);
}
}
}
int max = 0;
for ( i = 0; i <=N; i++)
{
if (Num[i] > max) max = Num[i];/*寻找最大的朋友圈*/
}
cout << max;
return 0;
}
- 线索二叉树:
1.储存结构:
typedef struct node
{ ElemType data; //结点数据域
int ltag,rtag; //增加的线索标记
struct node *lchild; //左孩子或线索指针
struct node *rchild; //右孩子或线索指针
} TBTNode; //线索树结点类型定义
2.操作方式
- 若结点有左子树,则lchild指向其左孩子,没有则指向它的前驱(线索)
- 若结点有右子树,则rchild指向其右孩子,没有则指向其后继(线索)
3.遍历方式图示
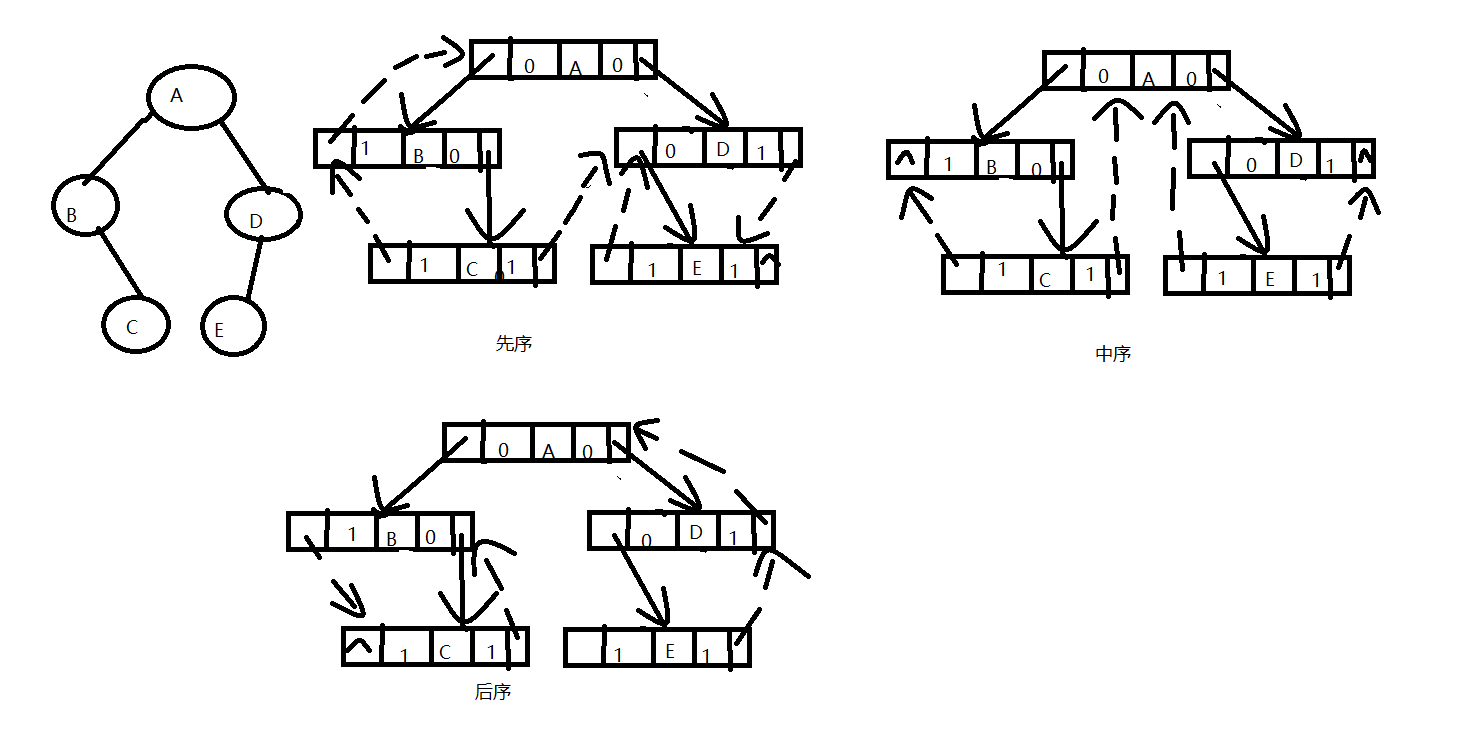
- 哈夫曼树
定义:给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。
带权路径长度:设二叉树具有n个带权值的叶结点,那么从根结点到各个叶结点的路径长度与相应结点权值的乘积的和,叫做二叉树的带权路径长度。
构建方法:
1.在二叉树集合T中选取根结点的权值最小和次小的两棵二叉树作为左、右子树构造一棵新的二叉树,这棵新的二叉树根结点的权值为其左、右子树根结点权值之和。
2.在集合T中删除作为左、右子树的两棵二叉树,并将新建立的二叉树加入到集合F中。
3.重复以上操作直到集合剩余一颗树。
例题:已知权值为W={3,4,5,6,9}
图解:
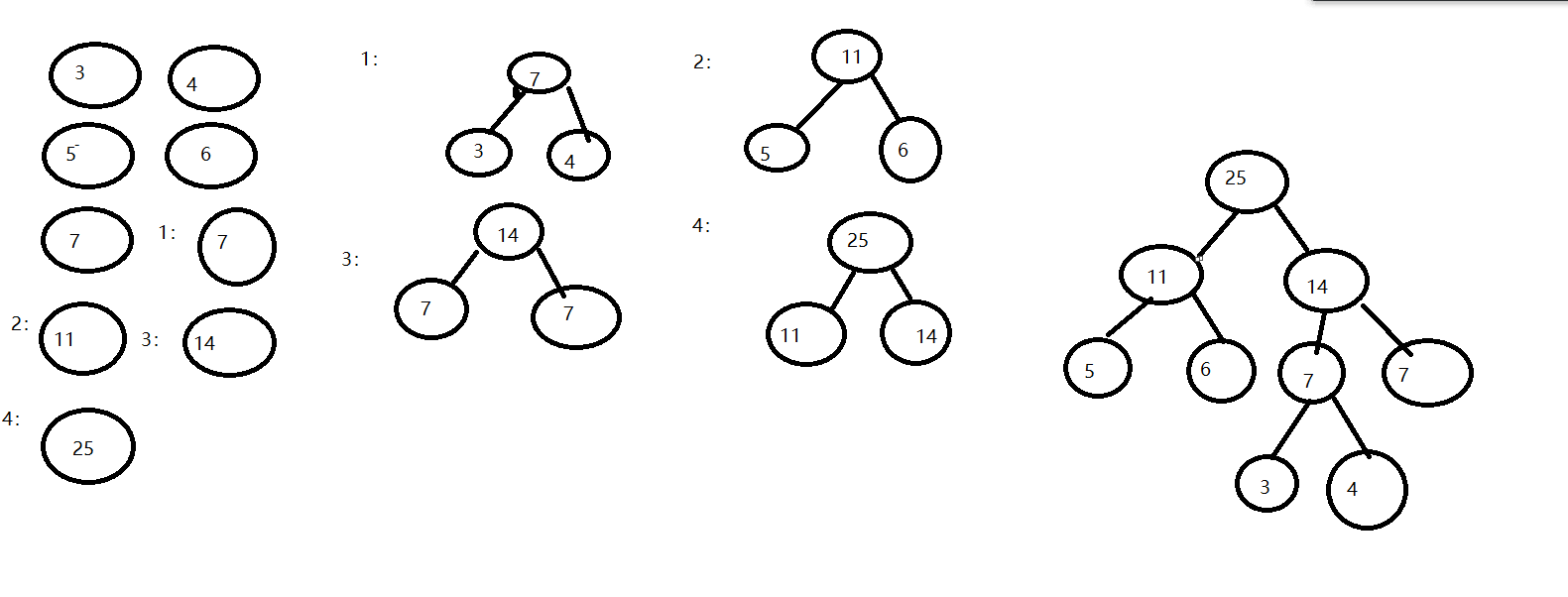
储存结构:
typedef s truct
{
char data;//节点值
float weight;// 权重
int parent;//双亲节点
int lchild;//左孩子节点
int rchild;//右孩子节点
}HTNode;
建哈曼夫树代码:
#include<iostream>
#define MAX 3000
using namespace std;
typedef struct
{
float weight;
int parent;
}HTNode;
void CreateHT(HTNode ht[], int n);
int main()
{
HTNode ht[MAX];
int i, n;
int wpl = 0;
cin >> n;
for (i = 0; i < n; i++)
{
cin >> ht[i].weight;
}
CreateHT(ht, n);
for (i = n; i < 2 * n - 1; i++)
{
wpl += ht[i].weight;
}
cout << wpl;
}
void CreateHT(HTNode ht[], int n)
{
int i, k;
int lnode, rnode;
float min1, min2;
for (i = 0; i < 2 * n - 1; i++)
{
ht[i].parent = -1;
}
for (i = n; i < 2 * n - 1; i++)
{
min1 = min2 = 9999999999;
lnode = rnode = -1;
for (k = 0; k <= i - 1; k++)
{
if (ht[k].parent == -1)
{
if (ht[k].weight < min1)
{
min2 = min1;
rnode = lnode;
min1 = ht[k].weight;
lnode = k;
}
else if (ht[k].weight < min2)
{
min2 = ht[k].weight;
rnode = k;
}
}
}
ht[lnode].parent = 1;
ht[rnode].parent = 1;
ht[i].weight = ht[lnode].weight + ht[rnode].weight;
}
}
- 并查集
定义:并查集是一种树型的数据结构,常用于处理一些不相交集合的合并及查询问题。
结构体定义:
typedef struct node
{
int data; //结点对应人的编号
int rank; //结点秩,大致为树的高度
int parent; //结点对应双亲下标
} UFSTree; //并查集树的结点类型
并查集操作
1:并查集的初始化:
void MakeSet(UFSLink t, int n)
{
int i;
for (i = 1;i <= n;i++)
{
t[i].data = i;
t[i].parent = i;
t[i].rank = 0;
}
}
2:查找集合归属:
int FindSet(UFSLink t, int x)
{
if (x != t[x].parent)
return FindSet(t, t[x].parent);
else return x;
}
3:合并集合:
void Union(UFSLink t, int x, int y)
{
x = FindSet(t, x);
y = FindSet(t, y);
if (t[x].rank > t[y].rank)
t[y].parent = x;
else
{
t[x].parent = y;
if (t[x].rank == t[y].rank)
t[y].rank++;
}
}
1.2对树的认识及学习体会
树的运用多建立在对递归算法的时候,所以在解题时方法是比较难思考的,且与栈与队列不同,并没有专门的头文件与专门的简便使用的特殊程序,于是对树的使用得一步步来自己书写,且树有着多样的遍历与创建方式,在面对题目时的可选方法越多,对正确方法的思索就越麻烦,而树的难点在于算法写完之后的查错是十分困难的,比单链队更复杂的结构导致面对程序出错时哪个步骤的出错是十分难查找的,需要不断的画图与推进才能发现错误。
但当对树的基本操作熟悉之后,对不同题目的解题的时候可以运用很多相同的函数来达成目的,树的操作也能简单不少。
2.阅读代码
2.1 题目及解题代码
题目:
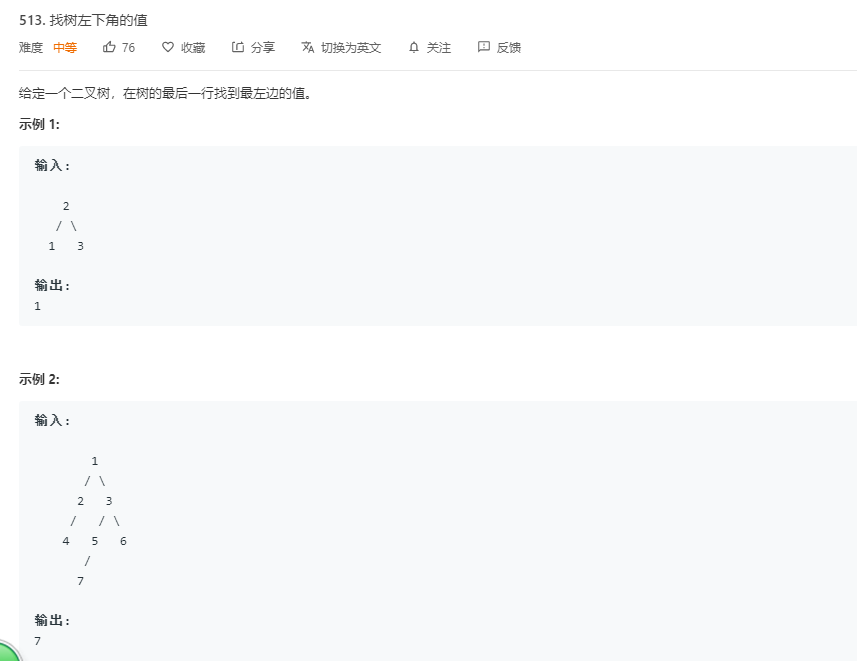
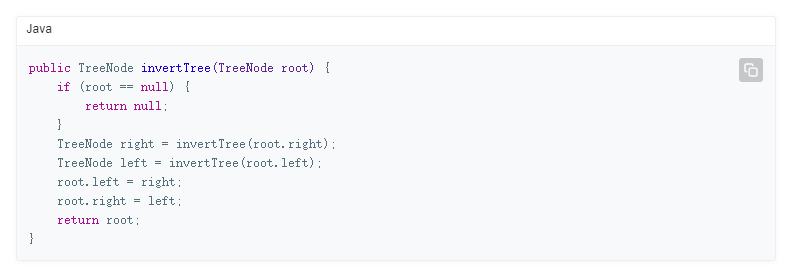
解题代码:

2.1.1该题的设计思路
图解:
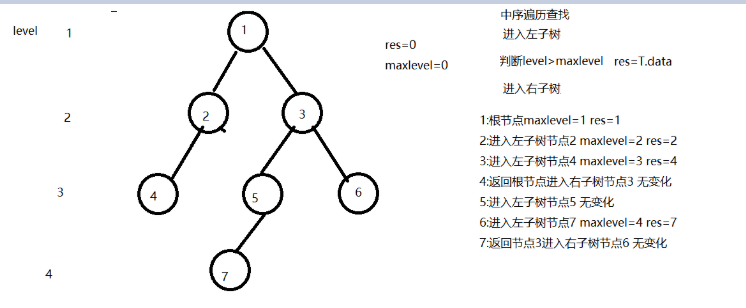
时间复杂度O(n);空间复杂度O(1);
2.1.2该题的伪代码
if 树为空
return 0
进入树的左节点;
if 该节点的深度>maxlevel
记录该结点的数值
进入树的右节点
2.1.3运行结果

2.1.4分析该题目解题优势及难点。
题目难点在于不是输出最左边的结点,而是输出最后一行最左边的结点,在判断时需要分析该节点是否为在最后一层,造成难点。
解题优势为不需要运用过多结构来记录数据,达成目的使用前序或中序来完成都可以,当时中序花费的时间最短,根据中序输出方式为最左边结点开始输出,与前序相比减少判断与记录数据的时间,代码也比较简单,只是对正常中序遍历的略微修改。
2.2 题目及解题代码
题目:

代码:

2.2.1该题的设计思路
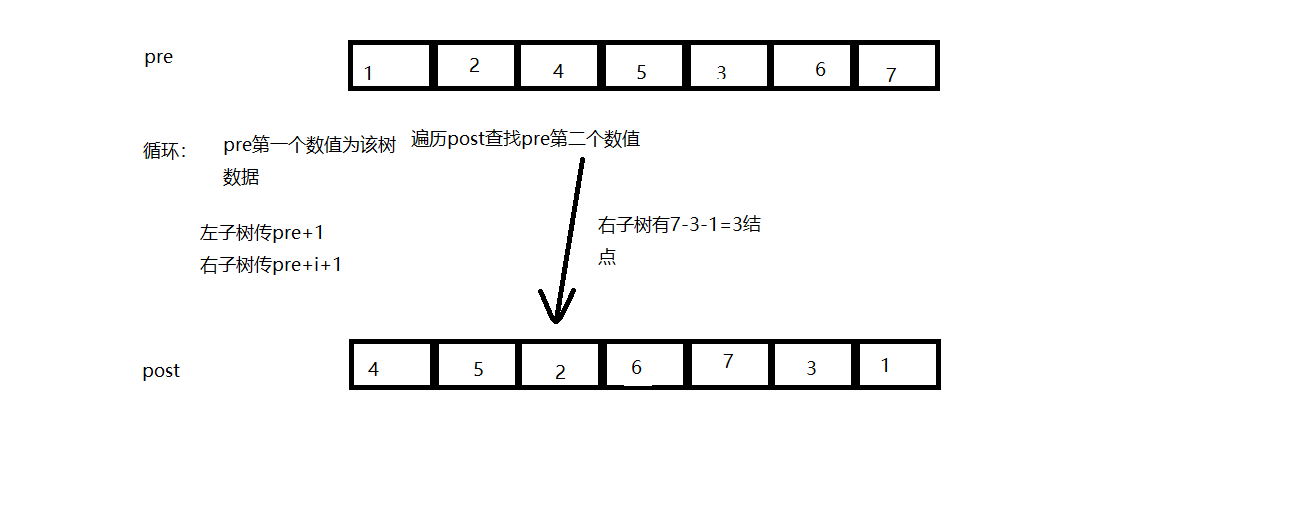
时间复杂度O(n2);空间复杂度O(n2);
2.2.2该题的伪代码
建立新树,左右结点为空
树数据为pre头位置数据
k为函数传值减1
if k==0
return 树T
遍历post查找*(pre+1)的值
i为post前进位置+1
树的左节点再次传函数,传值为pre+1,post,i
树的右节点再次传函数,传值为pre+i+1,post+i,k-i
2.2.3运行结果

2.2.4分析该题目解题优势及难点。
该题与已知两种遍历序列建树的解题方法相似,难点都在于对不同遍历序列的理解和如何分析哪些部分为左右子树,该题解题优势就是建树后再判断有无后序子树,无则直接返回树,有着继续左右子树建立,比在建立左右子树时判断是否为空减少了不少函数的建立。
2.3 题目及解题代码
题目:

代码:

2.3.1该题的设计思路
1:查找该节点左右子树,如果找到要找的树p与q,则返回树p与q,没找到则返回空树;
2:如果该节点只有一边返回p或q的值,这p,q都在该结点的一边的子树上或者已经找过其中一个树,则节点移到该子树节点在进行查找并返回找到的子树结果
3:如果该节点两边都有返回p或q树,则该节点是树p,q的最近祖宗返回该树。
时间复杂度O(n)空间复杂度O(n)
2.3.2该题的伪代码
if 结点T==p或结点T==q或结点T==NULL then
return 结点T
查找结点T左子树寻找树p,q
查到结点T右子树寻找树p,q
if T->left不为空&&T->right不为空判断该树为最近祖宗 then
返回结点T
if T->left不为空 then
返回结点T->left'
else
返回结点T->right;
2.3.3运行结果
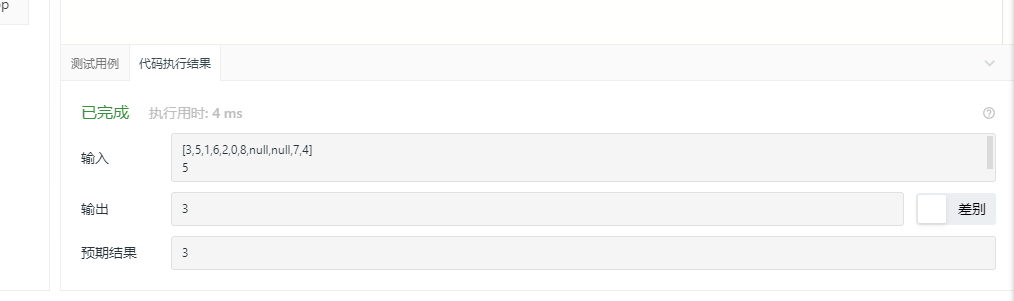
2.3.4分析该题目解题优势及难点。
该题难点在于解题方法的寻找,不好好分析树的结构则有可能往复杂的方式寻找,比如创建父子树来方便判断,而代码量就比较繁琐,这也是该解题方法的优势之处,通过判断结点左右子树是否分别存在一个要查找的结点来确定最近祖宗,代码写的也很简单与方便理解。
2.4 题目及解题代码
题目:
解题代码:
2.4.1该题的设计思路
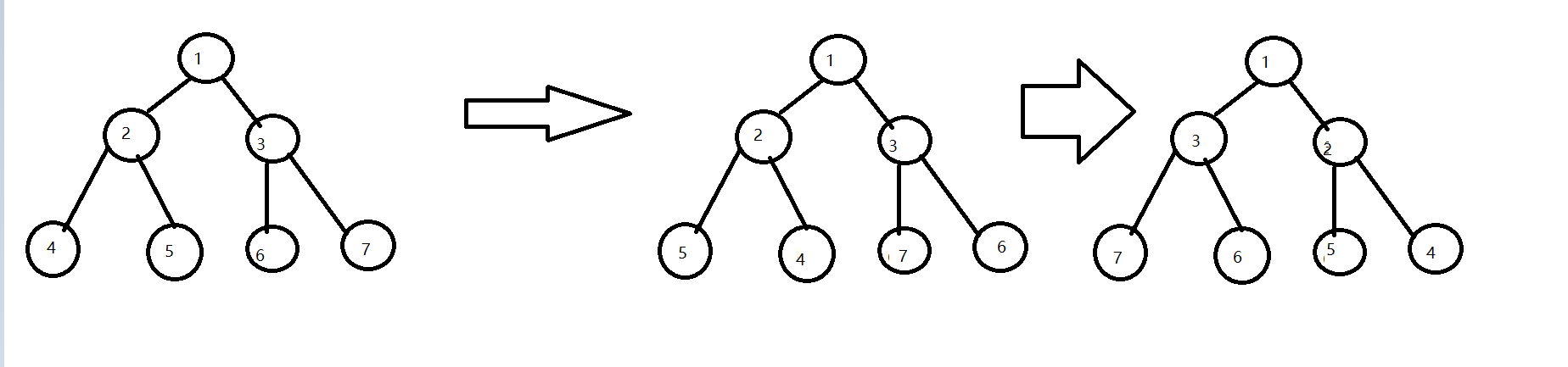
从叶子结点返回树,从下往上开始反转结点
时间复杂度O(n)空间复杂度O(n)
2.4.2该题的伪代码
遍历树直到叶子结点
返回该节点分别为right与left
返回上一节点使其左节点设为right右节点设为left
返回当前节点
2.4.3运行结果
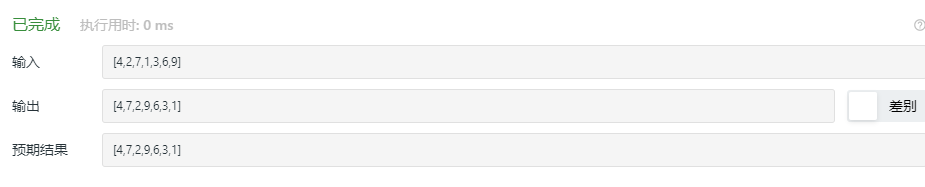
2.4.4分析该题目解题优势及难点
题目难度不高,重点在于解题方法的多样性,可以从根节点开始向下翻转或从叶子节点向上翻转都比较容易,解题优势在于从下往上翻转不必在于翻转后向下遍历时函数需要如何该改变,对代码的理解更方便简单。




