DS博客作业02--栈和队列
0.PTA得分截图

1.本周学习总结
1.1总结栈和队列内容
-
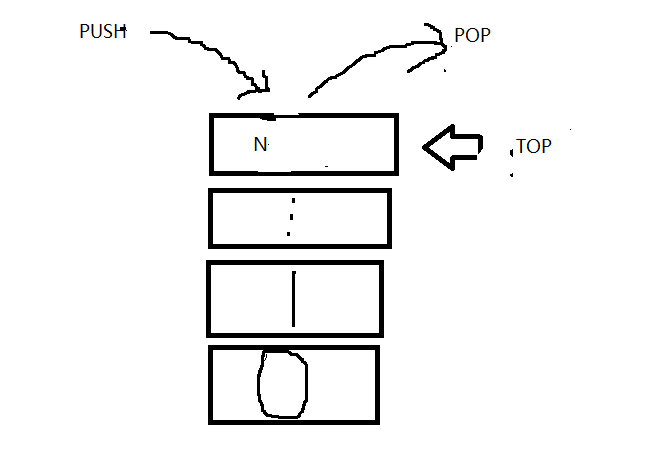
栈:一种操作受限的线性表,只允许在栈顶进行插入与删除操作,为进栈与出栈。
图解:
-
栈的存储结构:
1.栈的顺序储存结构
typedef struct
{
ElemType *base;//栈底
ElemType *top;//栈顶
int stackSize;//栈的当前可使用的最大容量
}sqStack;
2.栈的链式储存结构
typedef char ElemType;
typedef struct linknode
{
ElemType data;
struct linknode *next;
}LinkStNode;LinkStNode *s;
- 栈的操作
1.栈的初始化
顺序栈:
Stack CreateStack(int MaxSize)
{
Stack p = (Stack)malloc(sizeof(struct ST));
p->top = -1;
p->MaxSize = MaxSize;
return p;
}
链栈:
void InitStack(LinkStNode*&s)//初始化栈
{
s=(LinkStNode*)malloc(sizeof(LinkStNode));
s->next=NULL;
}
2.进栈操作:
顺序栈:
Status Push(SqStack *s, ElemType e) {
if (s->top == MAXSIZE - 1) { //栈满
return ERROR;
}
s->top ++;
s->data[s->top] = e;
return OK;
}
链栈:
void Push(LinkStNode*&s,ElemType e)
{
LinkStNode *p;
p=(LinkStNode*)malloc(sizeof(LinkStNode));
p->data=e;
p->next=s->next;
s->next=p;
}
图解:

出栈:
顺序栈:
Status Pop(SqStack *s, SElemType *e) {
if (s->top == -1) { //空栈
return ERROR;
}
*e = s->data[s->top];
s->top --;
return TRUE;
}
链栈:
void Pop(LinkStNode *&s)
{
LinkStNode *p;
while(s->next!=NULL)
{
p=s->next;
s->next=p->next;
free(p);
}
}
图解:
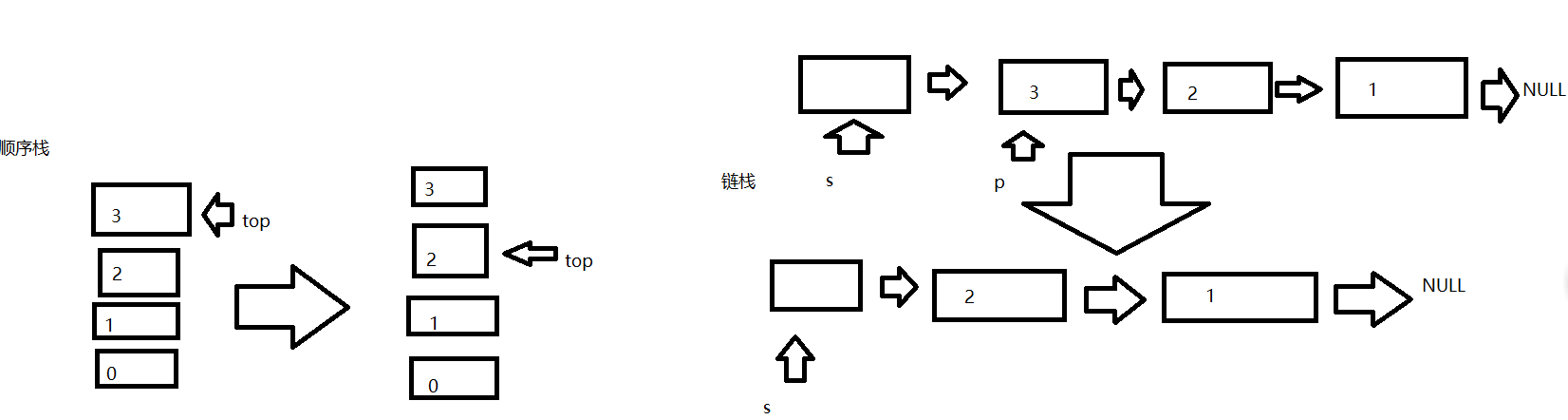
3.判断栈是否为空
顺序栈:
Status StackEmpty(SqStack S)
{
if(S.top == S.base)
return TRUE;
else
return FALSE;
}
链栈:
void StackEmpty(LinkStNode *s)
{
if(s->next==NULL)
{
cout<<"栈为空"<<endl;
}
else
cout<<"栈非空"<<endl;
}
- 栈的应用:
表达式转换
伪代码:
输入表达式;
初始化栈s;
int flag=1; /*判断正负号与输出前是否带空格*/
设定‘+’‘-’值为1‘*’‘/’号值为2‘(’值为0;
For i=0 to !str[i]
if 读入的为数字 then
if为第一个数字
输出数字
Flag=0
else
输出空格与数字
else if
if 数据为‘+’或‘-’且无数字输出
为正负号与后接数字一起输出
Continue;
End if
If 数据为‘(’且后接‘+’或‘-’
为正负号与后接数字一起输出
数据移动至’)’后
Continue;
End if
If 栈为空
数据入栈
Continue
End if
If读入数据为’(’
数据入栈s
End if
If读入数据为‘)’
数据出栈至’(’并输出(不输出’(’)
‘(’出栈
Continue
End if
If 读入数据的值大于栈顶数据的值
数据入栈
Continue
End if
If 读入数据小于或等于栈顶数据值
循环输出栈顶数据直到栈顶数据大于读入数据
读入数据入栈
End if
End if
Whie 栈不为空
输出栈内数据
出栈
End
代码:
#include<iostream>
#include<stack>
#include<string>
#include<map>
#define Max 25
using namespace std;
int main()
{
int i;
int flag = 1;
stack <char>s;
string str;
map<char, int>mp;
mp['+'] = 1;
mp['*'] = 2;
mp[ '-'] = 1;
mp[ '/'] = 2;
mp['('] = 0;
cin >> str;
for (i = 0; str[i]; i++)
{
if ((str[i] <= '9'&&str[i] >= '0') || str[i] == '.')
{
if (!flag)
{
cout << " ";
}
cout << str[i];
while (str[i + 1] == '.' || (str[i + 1] >= '0' && str[i + 1] <= '9'))
{
i++;
cout << str[i];
}
flag = 0;
}
else
{
if (flag&&mp[str[i]] == 1)
{
if (str[i] == '-')
{
cout << '-';
}
continue;
}
if (s.empty())
s.push(str[i]);
else {
if (str[i] == '('&&(str[i + 1] == '-'||str[i+1]=='+'))
{
if (str[i + 1] == '-') {
cout << ' ' << str[i + 1] << str[i + 2];
i = i + 3;
continue;
}
else
{
cout << ' ' << str[i + 2];
i = i + 3;
continue;
}
}
if (str[i] == '(')
{
s.push(str[i]);
continue;
}
if (str[i] == ')')
{
while (!s.empty()&&s.top() != '(')
{
cout <<' '<< s.top();
s.pop();
}
s.pop();
continue;
}
if (mp[str[i]] > mp[s.top()])
{
s.push(str[i]);
}
else
{
while ((!s.empty())&&mp[str[i]] <= mp[s.top()])
{
cout << ' ' << s.top();
s.pop();
}
s.push(str[i]);
}
}
}
}
while (!s.empty())
{
cout << ' ' << s.top();
s.pop();
}
}
-
队列:只允许在尾插入,头删除的结构。
图解:

-
队列的储存结构:
顺序队列
typedef struct{
int data[MAXQSIZE]; //容量
int front; //队头
int rear; //队尾
}SqQueue;
链队列
typedef int QElemType;
typedef struct QNode { //结点结构
QElemType data;
struct QNode *next;
}QNode;
typedef struct QNode * QueuePtr;
typedef struct {
QueuePtr rear; //指向尾位置
QueuePtr front; //作为头节点指向头位置前一个位置
}LinkQueue;
- 队列的操作:
1.初始化队列:
顺序队列
int InitQueue(SqQueue &Q) {
Q = new Queue; //为队列分配一个最大容量为MAXSIZE的数组空间
if (!Q->data)
exit( OVERFLOW); //存储分配失败
Q->front = Q->rear = 0; //头指针和尾指针置为零,队列为空
return OK;
}
链队列
void InitLinkQueue(LinkQueue* Q)
{
LinkQueueNode* pHead = (LinkQueueNode*)malloc(sizeof(LinkQueueNode));
assert(pHead);
Q->front = Q->rear = pHead; //队头和队尾指向头结点
Q->front->_next = NULL;
}
2入队列:
顺序循环队列
int EnQueue(SqQueue &Q, Person e)
{
if (((Q->rear + 1) % MAXQSIZE) == Q->front)return 0;
else
{
Q->rear = (Q->rear + 1) % MAXQSIZE;
Q->data[Q->rear] = e;
}
return 1;
}
链队列
void EnterLinkQueue(LinkQueue* LQ, DataType data)
{
LinkQueueNode* pNewNode = (LinkQueueNode*)malloc(sizeof(LinkQueueNode));
assert(pNewNode);
pNewNode->_data = data;
pNewNode->_next = NULL;
LQ->rear->_next = pNewNode;
LQ->rear = pNewNode;
}
图解:

3.出队列:
顺序循环队列
int DeQueue(SqQueue &Q, Person &e)//出队列
{
if (Q->rear == Q->front)return 0;
else
{
Q->front = (Q->front + 1) % MAXQSIZE;
e = Q->data[Q->front];
return 1;
\}
}
链队列
void DeleteLinkQueue(LinkQueue* LQ,DataType* data)
{
if (IsEmpty(LQ))
{
return false;
}
LinkQueueNode* pDel = LQ->front->_next;
*data = pDel->_data;
LQ->front->_next = pDel->_next;
if (LQ->rear = pDel)
{
LQ->rear = LQ->front;
}
free(pDel);
}
图解:
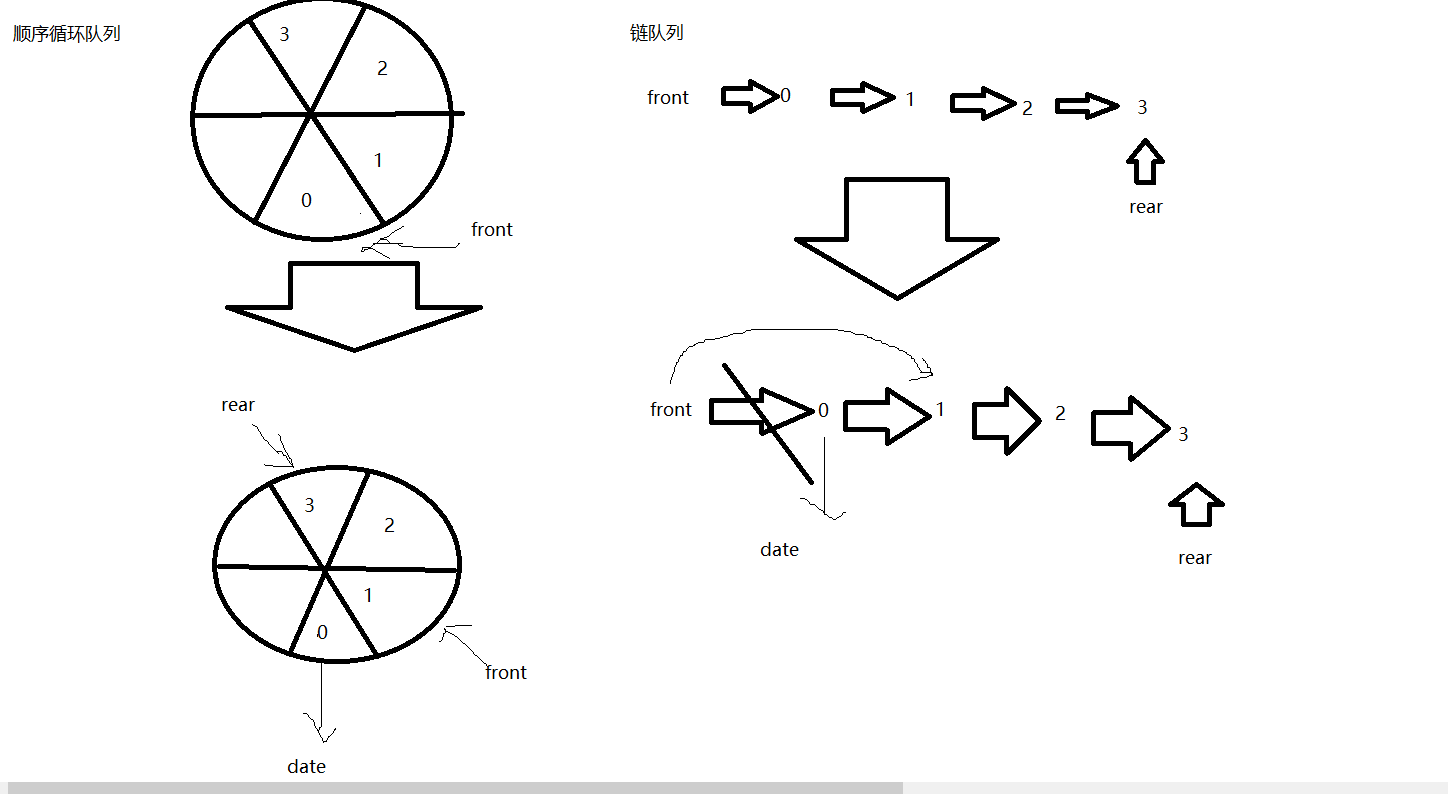
4.队空
顺序循环队列
int IsFull(SeqCirQueue* Q)
{
if ((Q->rear + 1) % MaxSize == Q->fornt)
{
return 1;
}
return 0;
}
链队列
int IsEmpty(SeqQueue* SQ)
{
if (SQ->fornt == SQ->rear)
{
return 1;
}
return 0;
}
- 队列的应用:
- 报数游戏
伪代码:
初始化队列s;
输入人数n与出队数字m;
if m>n
输出"error";
end if
for i=0 to i=n
i入队列s;
end
重置i=1;
while 队列s不为空
ifi%3==0 then
number取队列s头;
输出number;
队列s出队;
else
number取队列s头;
队列s出队;
number入队列s;
end if
i++;
end;
具体代码:
#include <iostream>
#include<queue>
using namespace std;
int main()
{
queue <int> s;
int i;
int number,flag=1;
int n, m;
cin >> n >> m;
if (n <= m)
{
cout << "error!";
return 0;
}
for (i = 1; i <= n; i++)
{
s.push(i);
}
i = 1;
while (1)
{
if (s.empty())
{
break;
}
number = s.front();
if (i%3==0)
{
if (flag)
{
cout << number;
flag = 0;
}
else
{
cout << " " << number;
}
s.pop();
}
else
{
s.pop();
s.push(number);
}
i++;
}
return 0;
}
1.2.谈谈你对栈和队列的认识及学习体会。
- 认识
栈和队列都是一种特殊的线性表,讲他们特殊化只是为了在处理特定类型问题的时候能够方便代码的写法,在理解代码的时候也能通过画图来方便掌握。 - 学习体会
栈和队列除了出数据的方式不一致,其他内容都有很多相似的地方,对他们的运用只需要记住一些操作方式的名词,多尝试几次就行。基础学习并不难,但多种方式的使用却需要需循渐进。
2.PTA实验作业
2.1 符号配对
2.1.1代码截图


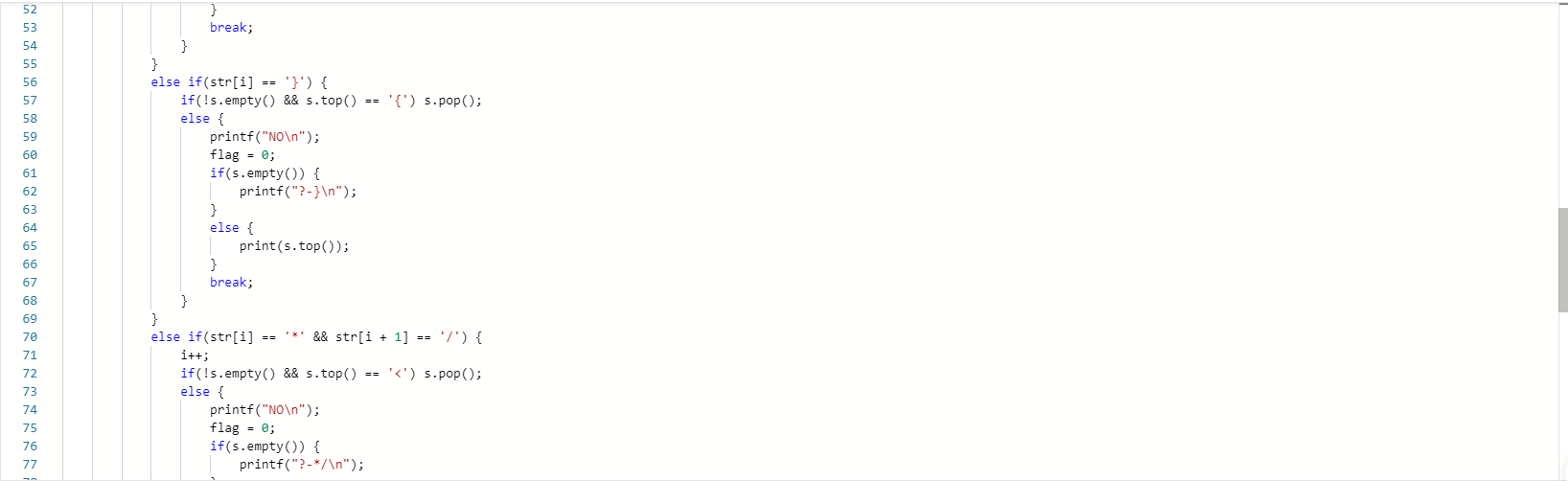

2.1.2本题PTA提交列表说明。
一开始的编译错误是提交的方式错了没选择c++,答案错误是最后一个测试点出错,发现之前代码在输出{缺失的情况,在某些情况会重复输出结果,后修改了输出方式才通过。
2.2银行排队问题之单队列多窗口服务
2.2.1代码截图



2.2.2本题PTA提交列表说明。
- 其中编程错误是有些在pta直接进行代码修改导致的错误。
- 部分正确为:一开始我只通过3个测试点,甚至认为pta给的示例数据是错的,后面认真审题才发现,当用户到达时间比窗口结束时间早的时候,他会选择序号最小的数字,而我一开始的写法则是选择最早结束的窗口。修改这之后便只剩下最后一个测试点没通过,之后我调试不出错误理由,就试了下网上的代码,并进行比较,之后在一次数据带入时发现第一次修改的代码依旧有点错误。
错误代码位置如下:

我if语句中的等号一开始是没有的,导致用户如果在窗口正好结束使用时进入,并不会被判定为最小序号窗口而直接选用,而是会进入比较窗口哪个早结束的语句中导致出错。
3.阅读代码
3.1题目及解题代码
题目:
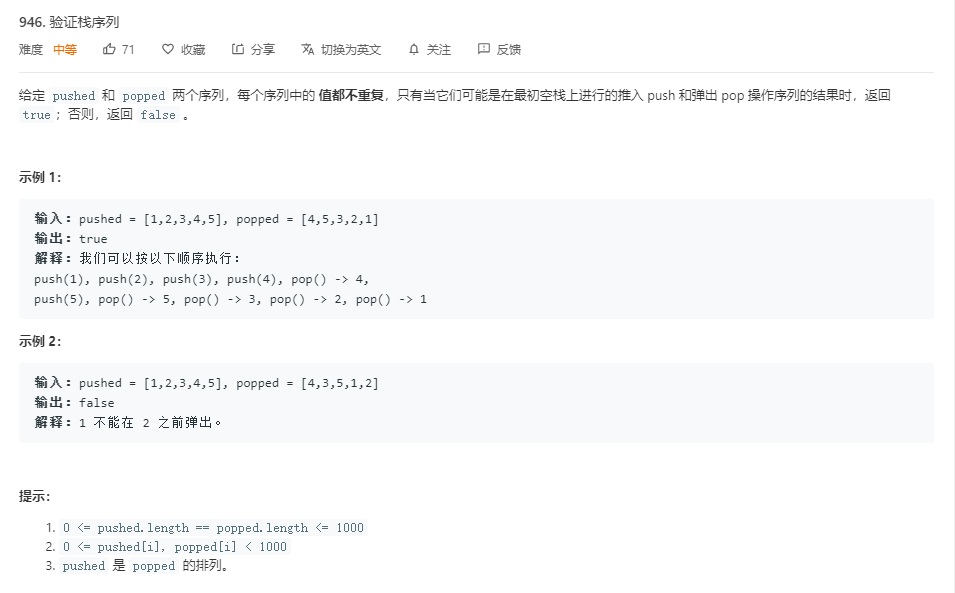
代码:
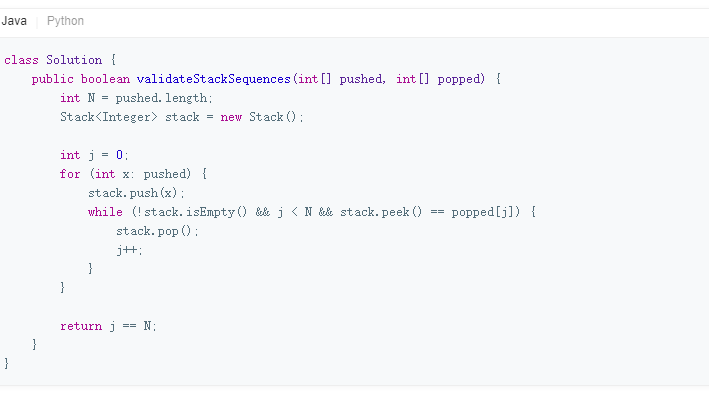
3.1.1 该题的设计思路
图解:
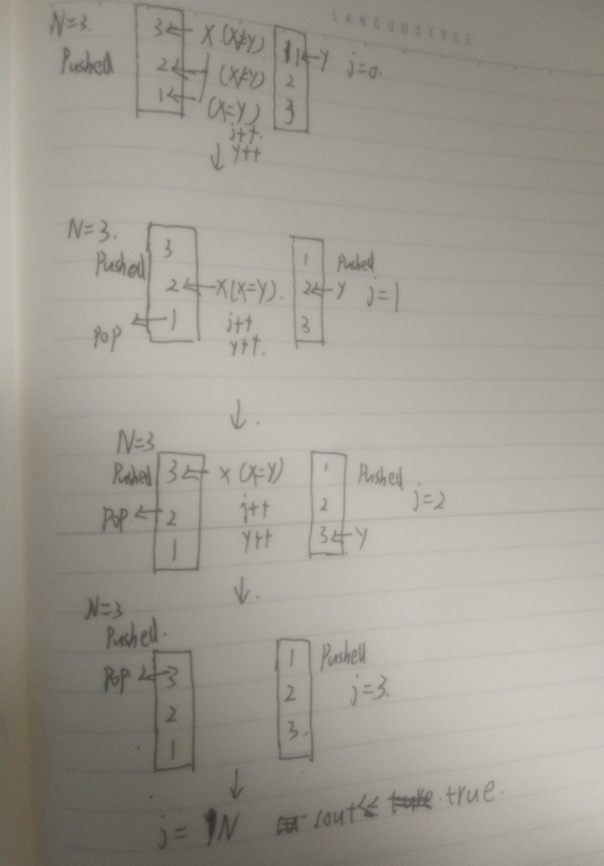
时间复杂度:O(N)
空间复杂度:O(N)
3.1.2伪代码
初始化栈s;
输入pushed内容至pushed数组
输入popped内容至popped数组
int数据j记录pupped数组位置
int数据m记录pushed数组元素个数
while pushed数组内容不为空
pushed数组数据入栈s
if 栈s顶等于popped数组元素 then
while 栈s不为空
if 栈s顶等于popped数组元素 then
s出栈;
j++;
else
break;
end if
if popped数组位置等于pushed数组个数
输出true;
else
输出false;
end if
3.1.3运行结果


3.1.4分析该题目解题优势及难点。
- 本题解题优势为对于数据的遍历较小,不需要多重循环来增加时间复杂度。
- 本题的难点在于题目对算法的要求表示的不明显,不依靠提示很难想到完成题目的流程。
3.2题目及解题代码
题目:
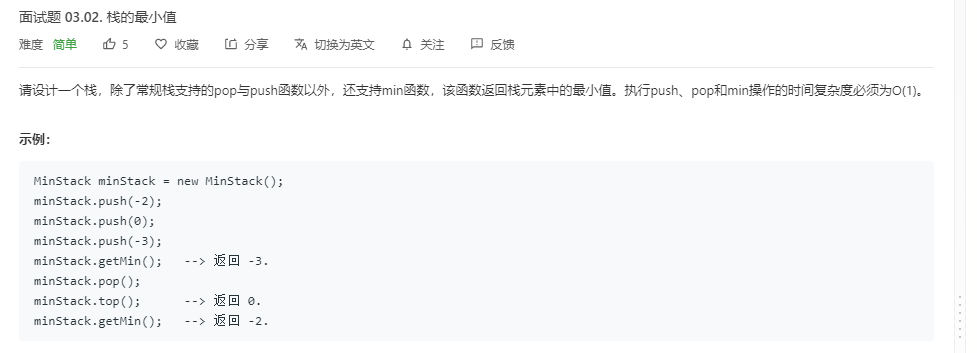
解题代码:
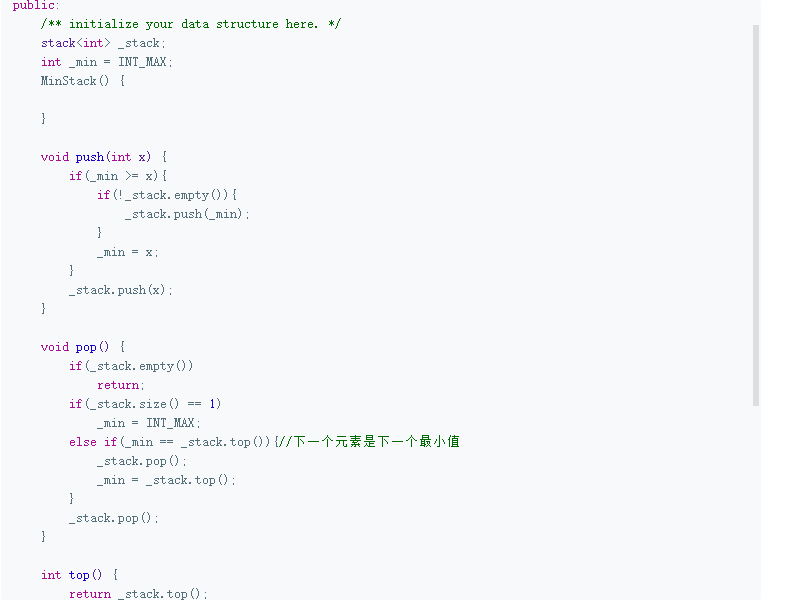
3.2.1 该题的设计思路
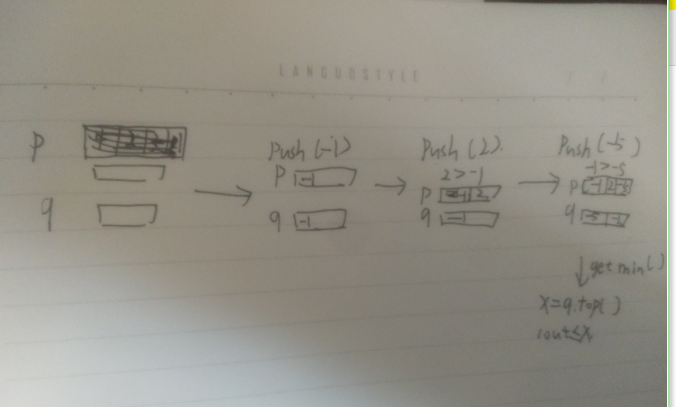
时间复杂度O(1)空间复杂度O(1)
3.2.2该题的伪代码
初始化栈p,q
if push(元素x)函数
if q为空 then
x入栈q;
else if x<栈q顶数据 then
x入栈q;
end if
x入栈p
if getmin()函数
x等于q栈顶元素
输出x;
end if
3.2.3运行结果

3.2.4分析该题目解题优势及难点。
- 该题解题优势在于设置新栈储存最小值,在每次入栈时对新入栈数据与最小值比较,判断是否更新最小值。
- 该题难度在于对时间复杂度与空间复杂度的要求限制





