C语言博客作业--数组
0.展示PTA总分



1.本章学习总结
1.1 学习内容总结
- 顺序查找法:从数组的第一个内容开始查找,直到找到要找值。
优点:写法简单易懂。
缺点:查找次数过多,面对大数据花费时间过长。 - 二分查找法:将数组排序后,从数组中间的数开始查找,当查找的数比中间的数大或者小的时候,取该数应处于的范围,再次取该范围中间的内容进行比较,直到找到正确的值。
- 数组的插入:先查找要插入的位置,后将该位置之后的元素全向后移动一位之后再将元素替换到该位置
#include<stdio.h>
int main()
{
输入要插入的数date;
输入要插入的数的位置i;
for j = n to j = i + 1;
a[j] = a[j - 1]; //将要插入数的位置之后的项的值赋予后面一项//
a[i] = date;
}
- 数组的删除
#include<stdio.h>
int main()
{
输入要删除的数据date;
for i = 0 to i < n;
for j = n to j >= i + 1;
查找要插入的数的位置i;
for j = i to j <n-1;
a[j] = a[j + 1]; //将要插入数的位置之后的项的值赋予前面一项,使该位置的的值被之后一位位置的值覆盖/
}
- 数组的排序方法:
1:选择排序法:依次查找最大的值位置,将他与被查找数组内容的第一个项给位置替换;
#include<stdio.h>
int main()
{
输入要排序的数组a[n];
for i = 0 to i < n;
{
for j = i to j < n;
{
int h = 0;
if (a[h] > a[j])
a[h] = a[j] //查找i位置之后的最小项//
}
temp = a[i];
a[i] = a[h];
a[h] = temp; //替换最小项与i位置//
}
}
2:冒泡排序法:多次查看数组,当出现前一个项比后一个项大时将该两项替换,是每次循环都能是最大的一个数移动到最末端,直到全部排序。
#include<stdio.h>
int main()
{
输入要排序的数组a[n];
for i = 0 to i < n-1;
{
for j = 0 to j < n-i-1;
{
if(a[j]>a[j+1])
temp = a[j];
a[j] = a[j+1];
a[j+!] = temp; //当出现前一项比后一项大时,替换两项位置//
}
}
}
- 数据枚举用法
调查电视节目受欢迎程度
#include<stdio.h>
#define N 9
int main()
{
int n;
int a[N];
int i, j;
for (i = 0; i < N; i++)
{
a[i] = 0;
}
scanf("%d", &n);
for (i = 1; i <= n; i++)
{
scanf("%d", &j);
if (j<9)
{
a[j]++;
}
}
for (i = 1; i < N; i++)
{
printf("%4d%4d\n", i, a[i]);
}
}
- 哈希数组用法
有重复的数据I
#include<stdio.h>
#define N 100001
int check(int n);
int main()
{
int n;
scanf("%d", &n);
if (check(n) == 1)
{
printf("YES");
}
else
{
printf("NO");
}
return 0;
}
int check(int n)
{
int static num[100001];
int i;
int x;
for (i = 1; i <= n; i++)
{
scanf("%d", &x);
if (num[x] == 1)
{
return 1;
}
else
{
num[x]=1;
}
}
return 0;
}
1.2 本章学习体会
- 数组多用在储存大数据,当面对多个数据需要保存是不需要写多个变量一一保存,节省代码量,且对数据进行排序,删除等操作也十分简便。
- 两周代码量:2500
2.PTA实验作业
2.1 7-5 有重复的数据I
2.1.1 伪代码
#include<stdio.h>
#define N 100001
int check(int n);
int main()
{
输入要输入的数字个数n;
if (check(n) == 1) //判段输入的数是否有重复数据//
{
printf("YES");
}
else
{
printf("NO");
}
return 0;
}
int check(int n)
{
int static num[100001];
int i;
for i=0 to i<=n
{
输入数字x;
if (num[x] == 1) //如果该数字作为下标对应的数组的值为1,则该数字以存在过//
{
return 1;
}
else
{
num[x] = 1; //如果该数字还未出现过,则将该数字作为下标对应的数组的值赋值为1,表示该数字存在过//
}
}
return 0;
}
2.1.2 代码截图
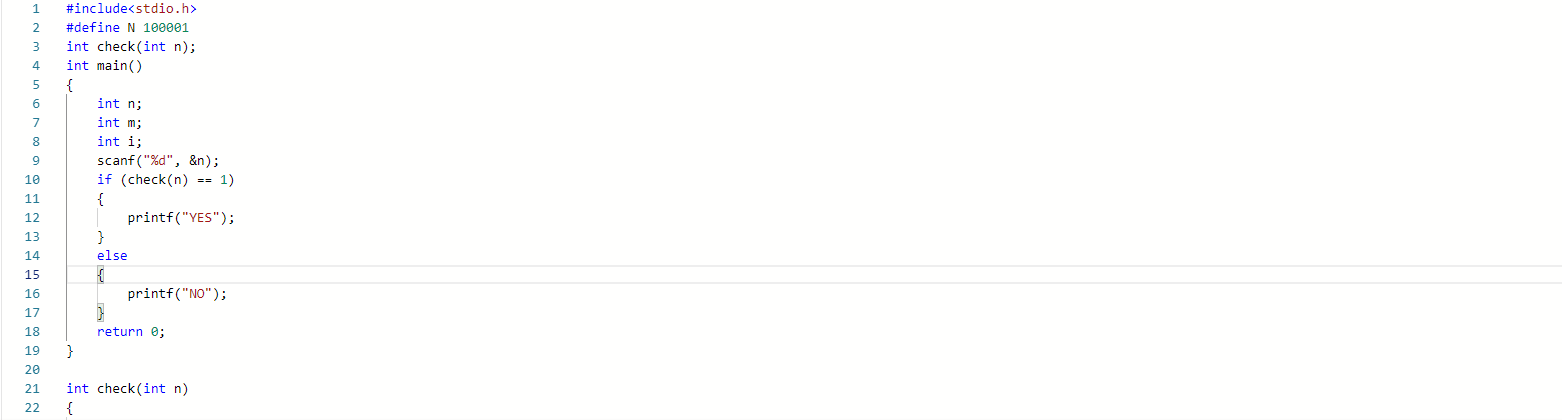

2.1.3 造测试数据
| 输入数字个数 | 输入数字 | 结果 |
|---|---|---|
| 5 | 1 2 3 1 4 | YES |
| 10 | 10 1 7 5 6 -3 9 7 6 1 13 | YES |
| 5 | 1 3 5 7 9 | NO |
2.1.4 PTA提交列表及说明
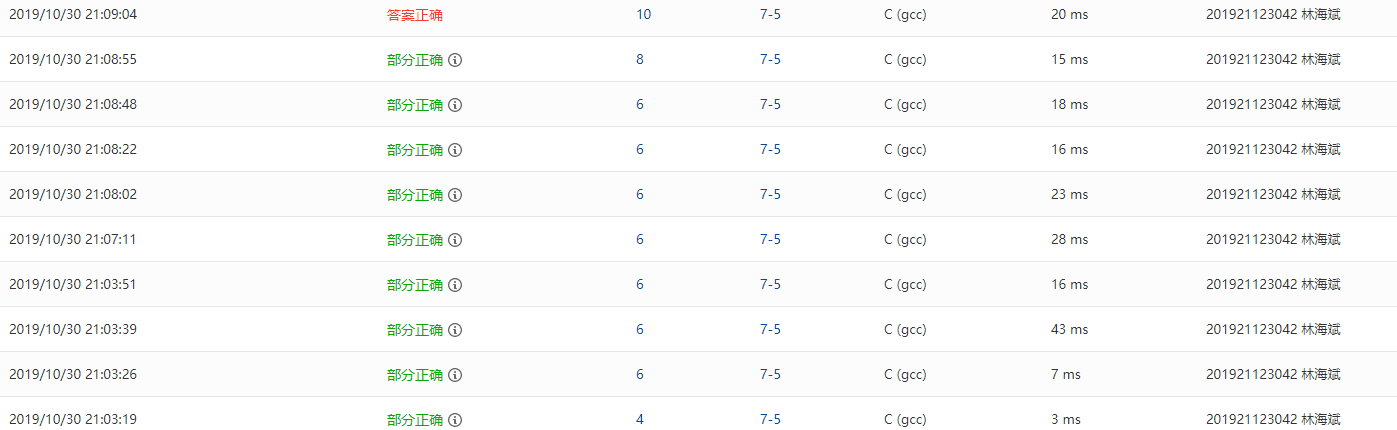
原来是用两层单循环进行数据查重,由于数组的长度设定太小,调整之后分数增加一些,但最后两个测试点依旧是错的。
最后就仿照超星平台的做法改了代码。
2.2切分表达式——写个tokenizer吧
2.2.1 伪代码
#include<stdio.h>
#include<string.h>
#define H 80
int main()
{
输入字符串a[H]:
for i=0 to a[i]!='\0';
{
if (a[i] >= '0'&&a[i] <= '9')//当输入为数字时直接输出//
{
printf("%c", a[i]);
if (a[i + 1] == '.')//判断该数是否为小数//
{
i++;
printf("%c", a[i]);
}
while (a[++i] >= '0'&&a[i] <= '9')
{
printf("%c", a[i]); //输出全部数字后换行//
}
i = i - 1;
printf("\n");
}
if (a[i] == '*' || a[i] == '/' || a[i] == '(' || a[i] == ')'||a[i]=='=')
{
printf("%c\n", a[i]); //当遇到某些符号时直接输出并换行//
}
if (a[i] == '-' || a[i] == '+')
{
if (a[i - 1] == '(' || i == 0)
{
printf("%c", a[i]); //判断该‘-’号或‘+’号是作为运算符号还是作为数的前标判断正负//
while (a[++i] >= '0'&&a[i] <= '9')
{
printf("%c", a[i]);
if (a[i + 1] == '.')
{
i++;
printf("%c", a[i]);
}
}
i = i - 1;
printf("\n");
}
else
{
printf("%c\n", a[i]);
}
}
}
}
2.2.2 代码截图
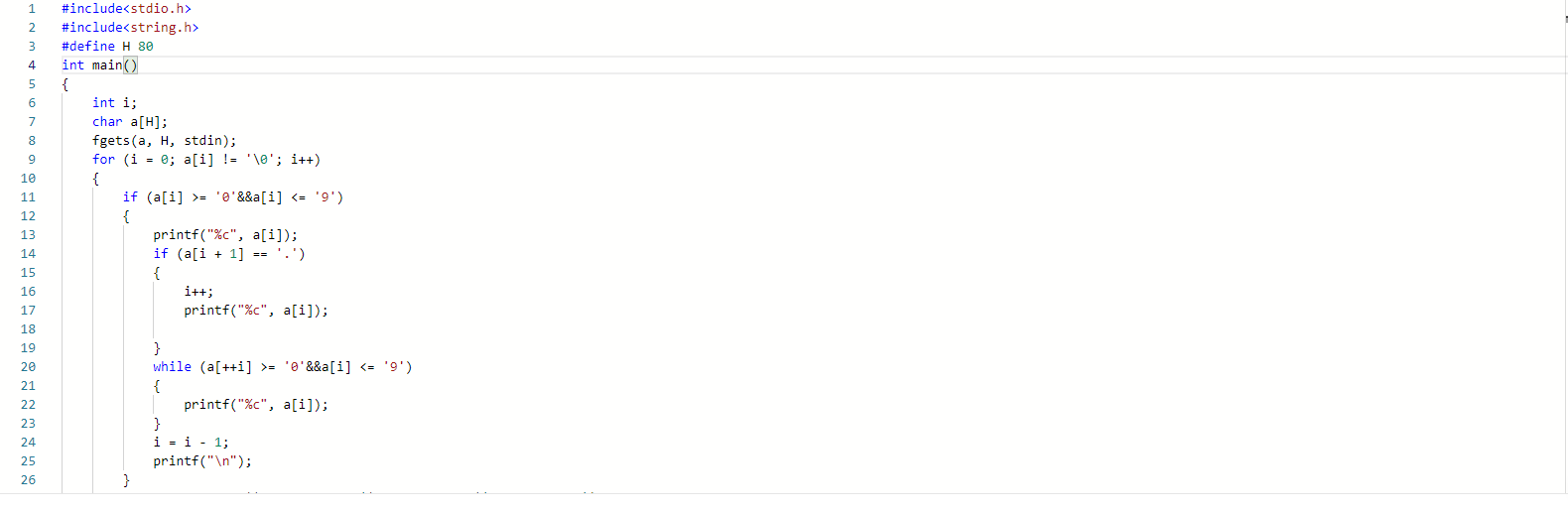

2.2.3造测试数据
| 输入 | 输出 |
|---|---|
| 32*((2-2)+5)/(-15) | 32 * ( ( 2 - 2 ) + 5 ) / ( -15 ) |
| -0.735/2(-0.89) | -0.73 * 5 / 2 * ( —-0.89 ) |
2.2.4 PTA提交列表及说明
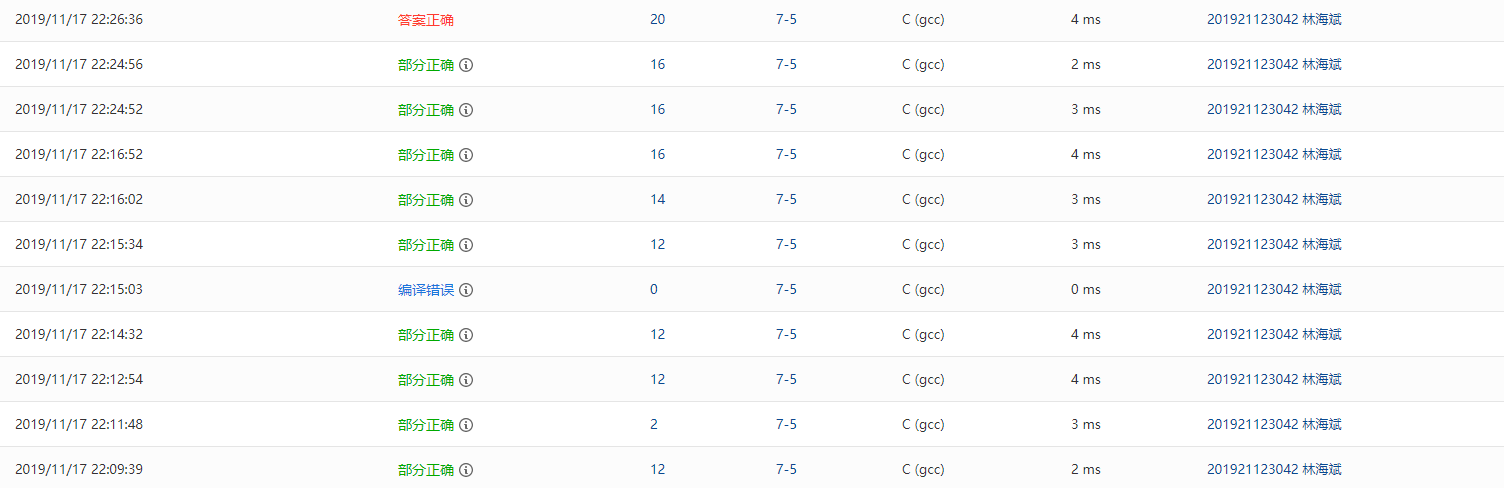
编程错误是改的时候写错就交了
一开始答案错误包括没计算小数,当正号是作为数字的符号的情况没判断,当负号再输入开头是没判断,以及符号作为数字符号,且数字为小数的情况,只能输出整数部分又改了几次。
2.3螺旋方阵
2.3.1伪代码
#include<stdio.h>;
#define M 10
int main()
{
int flag = 1;//判断该从哪个方向进行赋值//
int i=0,j=0;
int count ;
int N;
static int a[M][M];
scanf("%d", &N);
count = N;
a[0][0] = 1;
while (flag<=2*N-1) //根据输入的几节方针判断循环的次数//
{
if (flag%4==1) //以4次循环为一次重复当进行一次循环的时候,将数组列下标递增直到n,前后赋值的数都为前一个数的加1//
{
while (j<count-1)//由于循环的一开始作为头的第一个数已经被赋值则循环次数减1//
{
j++;
a[i][j] = a[i][j - 1] + 1;
}
flag++;
}
if (flag%4==2)//第二次循环则行下标递增,赋予的值依旧递增//
{
while (i<count-1)
{
i++;
a[i][j] = a[i - 1][j] + 1;
}
flag++;
}
if (flag%4==3)//当第3次循环时列下标递减,赋予的值递增,最后由于下一次循环头和尾都依旧被赋值,将递减的次数减1//
{
while (j > N-count)
{
j--;
a[i][j] = a[i][j + 1] + 1;
}
flag++;
count = count - 1;
}
if (flag%4==0)
{
while (i > N - count)
{
i--;
a[i][j] = a[i + 1][j] + 1;
}
flag++;
}
}
for i =0 to i<n;
for j=0 to j< n;
输出数组;
}
2.3.2 代码截图



2.3.3测试数据


2.3.4 PTA提交列表及说明

一开始并不会做这题目,只能根据最外圈的数字找规律,后自己写了几个不同大小的螺旋方阵判断了要拐角的次数,又发现自己写的最外圈的代码只要根据拐角次数就可以完成程序,个人认为这题还是蛮难看出代码的。
3.阅读代码

该程序的要求是确认该数组是否为山脉数组,该代码是查找整个数组是否存在一个项比他的下一个项的值大,如果存在,则说明这个数组的值存在一个顶点,这个顶点不一定是这个数组最大的一个数,而是他比左右两边的项的值都大,使数组不满足单调递增或单调递减的项,存在这个项这说明该数组是个山脉数组。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号