浅谈哈希表
哈希表
哈希表（Hash table，也叫散列表），是根据关键码值(Key value)而直接进行访问的数据结构。
也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做哈希函数，存放记录的数组叫做哈希表。
给定表M，存在函数f(key)，对任意给定的关键字值key，代入函数后若能得到包含该关键字的记录在表中的地址，则称表M为哈希(Hash）表，函数f(key)为哈希(Hash) 函数。
哈希表的构建方法
哈希函数是重心！
哈希函数
哈希函数是根据关键字/元素设计的，有很多种函数，其一就是根据数组的大小求模运算
（关键字）%（数组大小）
例如：20048157%17（结果肯定在0~16之间）
由于需要将元素/数据均匀分布至设计的哈希表中，故数组的大小一般设计为质数。
解决冲突
1、链表式解决法
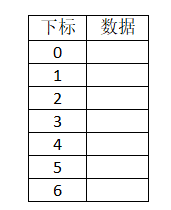数组关键字/元素/数据： 15 22 24 16
数组大小：7
哈希函数： 下标 = 关键字 mod 7
哈希函数后存放至哈希表中的结果如下：
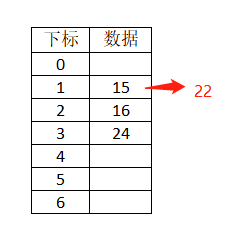
2、开放地址(把其他下标VDE地址均对外开放)
a、线性探测法
如果遇到冲突，就往下一个位置寻找空位。
如果遇到冲突，新位置 = 原始位置 + i（i是指发生冲突的次数）去寻找空位
例如：
数据关键字： 15 2 38 28 4 12
数组大小：13
哈希函数：下标 = 关键字 mod 13
哈希函数后存放至哈希表中的结果如下：
解释：首先15 mod 13，其结果为2，下标为2的位置正好空着，将该关键字放入该位置，下一个关键字 2 mod 38 其结果也为2，
在数组中不能发现下标为2的位置已经被占据，故放到下一位置，也即下标为3的位置，以此类推。
注：12 mod 13结果为12，但是38占了下标为12这个位置，故应该将12存放至下一位置，也即存放至下标为0的位置。
b、平方探测法
如果遇到冲突，新位置 = 原始位置 + i^2（i是指发生冲突的次数）去寻找空位
数据关键字： 15 2 28 19 10
数组大小： 13
哈希函数：下标 = 关键字 mod 13
哈希函数后存放至哈希表中的结果如下：
较线性探测法，避免了数据扎堆的弊端！
c、双哈希
要设置第二个哈希函数，例如：hash2（key）= R - （key mod R）
R要取比数组尺寸小的质数。
例如： 取R=7， hash2（key）= 7 - （key mod 7）
也就是说，二次哈希的结果在1~7之间，不会等于0，因为加0等于没加！
如果遇到冲突，新位置 = 原始位置 + i * hash2（key）
数据关键字： 15 2 18 28
数组大小： 13
哈希函数：下标 = 关键字 mod 13
哈希函数：7 - （关键字 mod 7）
如果遇到冲突，新位置 = 原始位置 + i * hash2（key）
哈希函数后存放至哈希表中的结果如下：
注意：此处容易犯错，容易直接将关键字安排在哈希函数2得到的结果上，应该是原位置 + i * 哈希函数2得到的结果！
哈希表满了怎么办？
再次哈希
* 当哈希表数据存储量超70%，那么就自动新建一个新的哈希表
* 新表的尺寸应该为旧表尺寸的2倍以上，选择一个质数作为新表的尺寸
* 把之前的数据再次通过新表尺寸进行哈希计算搬到新表里！
哈希表的优劣：
优势：
查找性能高，条件允许情况下比搜索二叉树还高！
搜索二叉树查找速度：O（log N）
发挥稳定时，搜索速度可达：O(1)
劣势：
表越满，越容易发生冲突，性能越差
