数学建模方法-遗传算法(理论篇)

一、引言

　　哈喽大家好，今天要给大家讲的是“遗传算法”。跟粒子群算法、蚁群算法一样，遗传算法也是属于启发式算法，它基于达尔文的进化论，模拟进化论中的“自然选择，物竞天择、适者生存”，通过N代的遗传、变异、交叉、复制，进化出问题的最优解。

二、浅谈生物学

2.1  达尔文教你进化论

　　学过初中生物的应该都知道达尔文的进化论。总结起来其实就是“物竞天择、适者生存”。这是什么意思呢？通俗讲，就是在弱肉强食的时代，唯有强者才能生存下来。记住这句话，这是遗传算法的核心。

2.2  遗传学所告诉我们的

　　好，达尔文告诉我们要生存下去就要适应环境，但是如何它没告诉我们存活下来的生物是如何不被淘汰的。遗传学告诉了我们答案。我们知道，细胞是所有生物的基石。对于每个细胞，都有一套相同的染色体，而染色体，则是由DNA所聚合而成，其中DNA又是由基因组成的。每个基因都编码了一个独特的性状，比如头发或眼皮的颜色。如下图：

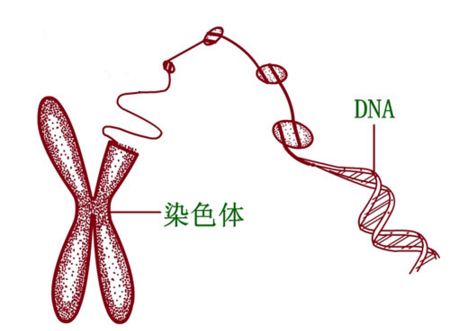
　　我们假设在某个地区O，生活着两类生物，其中携带基因a的生物种群P能够适应当前的自然环境，携带基因b的生物种群Q不能够适应当前的自然环境。因此，随着岁月的流逝，那些不能适应当前自然环境的生物一个个死去，而能够适应当前自然环境的生物不断的繁衍。很多年很多年过去后，这个地区O留下来的都是携带基因a的生物种群P。

　　好了，生物学知识暂且讲到这里，足够我们接下来解释我们的遗传算法了。

三、遗传算法

3.1  遗传算法的定义

　　我们把种群P当成问题的最优解，把除P外的种群当成普通解。那么进化就是普通解不断被淘汰而最后留下的只有最优解的过程。这就是遗传算法的思想。我们先给出遗传算法的流程如下，具体在后面解释：

　　1. 种群初始化
　　2. 计算每个种群的适应度值
　　3. 选择(Selection)
　　4. 交叉(Crossover)
　　5. 变异(Mutation)
　　6. 重复2-5步直至达到进化次数

　　现在，我们来逐步理解一下整个流程。

3.2 遗传算法的具体步骤

　　讲步骤的时候可不能少了例子，这次我们利用遗传算法来解决一个著名的问题——背包问题。背包问题是这样子的：大家知道荒野求生的贝爷么，不知道的百度hh，是一个站在食物链最顶层的男人。贝爷决定去一个荒岛开始它一个月的野外生活。但是它只有一个只能放35kg的背包。现在，它有不同的野外求生必需物品，每类物品都有其对应的生存点数（具体在下表给出）。那么，问题就是，如何在有限的背包重量下，最大化贝爷的生存点数。

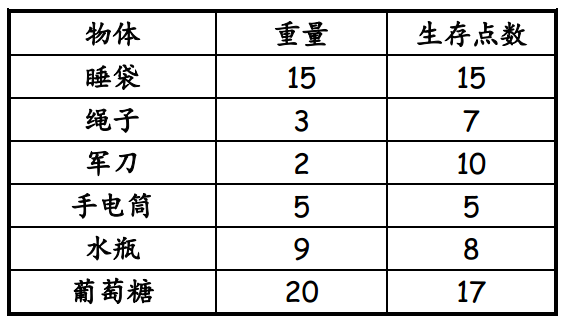
　　(1) 初始化

　　首先我们要先我们要进化的种群，每个种群的个体都有一套自己的染色体。染色体则由基因组成。因此，一般的，我们的染色体可表达为二进制数串。在“背包问题”中，1代表基因存在，0表示基因缺失。在特定位置上的基因代表了上方表格中物体，如表中第一行是睡袋，那么对应的染色体上的左边第一个基因位置就是描述睡袋的。如图：　　

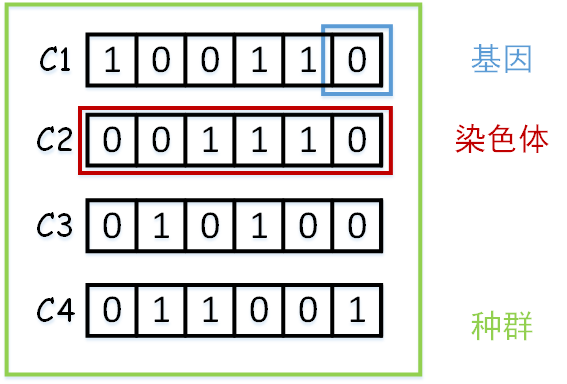
　　我们假定一开始只有4个个体，每个个体的染色体分别为C1-C4。那么这四个个体构成我们的一个种群。

　　(2) 对每个个体计算其适应度值

　　适应度值，fitness value。在前面几篇文章都出现过，是用于确定个体好坏的一个评价准则。在这个背包问题中，生存点数高就是个体好，因此这个个体的生存点数就是个体的适应度值。

　　对于C1染色体[100110]，其fitness value为：

$fitVal(C_{1}) = 1 \times 15 + 0 \times 7 + 0 \times 10 + 1 \times 5 + 1 \times 8 + 0 \times 17 = 28$

　　对于C2染色体[001110]，其fitness value为：

$fitVal(C_{2}) = 0 \times 15 + 0 \times 7 + 1 \times 10 + 1 \times 5 + 1 \times 8 + 0 \times 17 = 23$

　　对于C3染色体[010100]，其fitness value为：

$fitVal(C_{3}) = 0 \times 15 + 1 \times 7 + 0 \times 10 + 1 \times 5 + 0 \times 8 + 0 \times 17 = 12$

　　对于C4染色体[011001]，其fitness value为：

$fitVal(C_{4}) = 0 \times 15 + 1 \times 7 + 1 \times 10 + 0 \times 5 + 0 \times 8 + 1 \times 17 = 34$

　　显然，含有染色体C4的个体生存点数更高，适应性最强。

　　(3) 选择(selection)

　　接下来我们就是要选择要进行“交配”的染色体了，我们的目的是为了产生优良的下一代，因此选择“交配”的染色体自然也是要优良的。因此我们应该选择生存点数较高的C4染色体和C1染色体，对吧。这样想没错，但是这样的话在几代后染色体之间的相互差异就减少，失去多样性了。因此，我们一般会往里面假如一些随机性。让选择也具有一些随机性。那怎么加入呢？一般是采用轮盘赌选择法。在前面的文章也出现了轮盘赌选择法，但是那时我没有解释。现在来解释下：

　　假设有一个轮盘，我们把它分割成n份(n表示总体中染色体的个数)，每条染色体在轮盘上的占用面积跟它的适应值成正比。以前面的例子来看，应如下图：

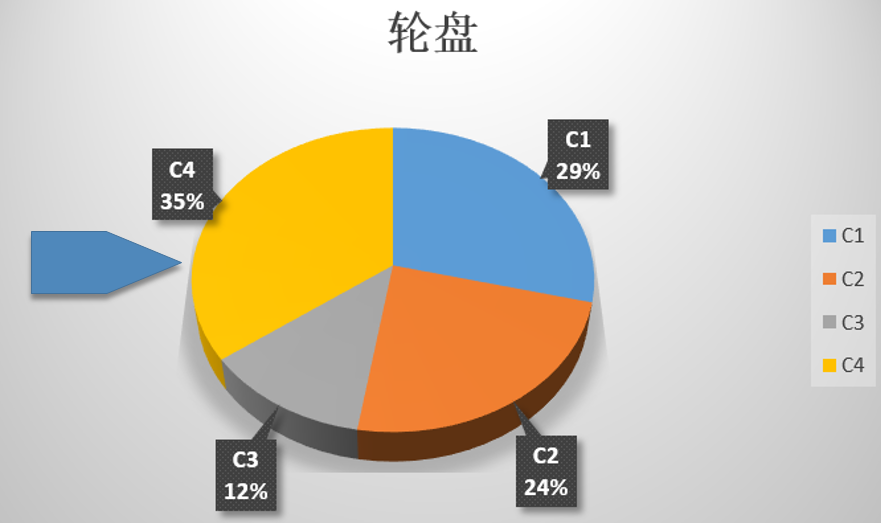
　　现在，将这个轮盘进行旋转，当停下来的时候，指针指中的那片区域所代表的染色体即为第一个亲本，重复操作得到第二个亲本。选中这两个亲本进行“交配”产生下一代。

　　(4) 交叉(crossover)

　　好了我们已经选择可以产生后代的亲本染色体了，接下来就是要“交配”了。诶诶怎么交配，其实这里的交配指的是染色体交叉互换，其中根据交叉点的个数可分为单点交叉和多点交叉。

　　单点交叉：交叉最基本的形式，随机选择一个交叉点，将交叉点前后的染色体部分进行染色体间的交叉对调从而产生新后代，如下图：

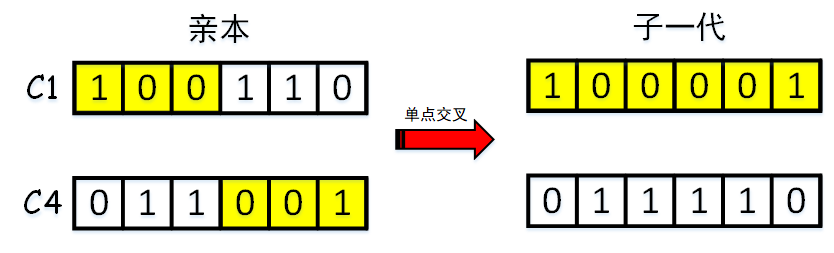
 　　多点交叉：选择两个交叉点，将交叉点之间的染色体部分进行对调从而产生后代，如下图：

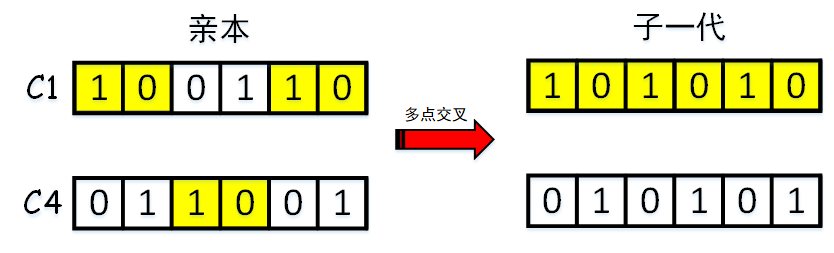
  　　(5) 变异(mutation)

　　在生物学中，在后代的生长过程中，它们体内的基因会发生一些变化，使得它们与父母不同，这个过程我们称为变异。变异是导致子一代的性状与亲一代不一样的原因。也就是说，正是因为变异，才导致种群存在多样性。

　　一般的，我们定义变异为染色体上发生的随机变化。如下图：

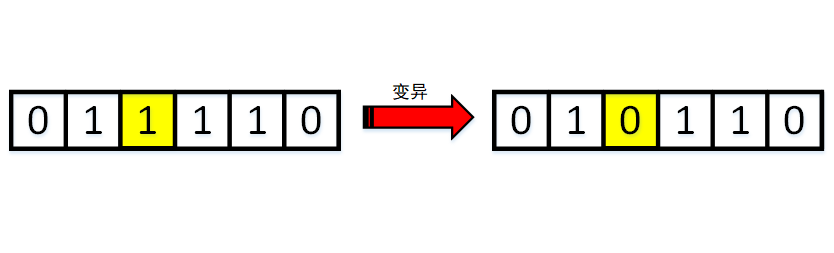
　　变异完成后，我们就得到了新的个体，完成一次进化。整个过程如下图（图来源：http://www.jade-cheng.com/au/coalhmm/optimization/）：

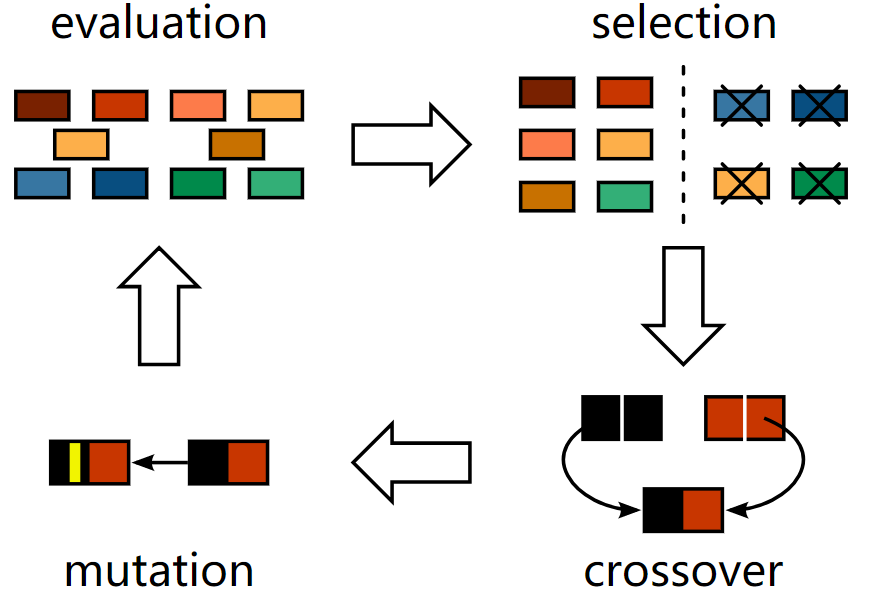
　　这样就算完成了一次进化，接着我们由要用适应度函数去对这些新的后代进行判定，如果后代的适应度值够大，则将其替代掉总体中那些适应度值较低的染色体（保证种群的个数不变）。接着不断重复选择-交叉-变异这几个步骤，直至达到进化次数。