1 2 3 4

20172310 2017-2018《程序设计与数据结构》（下）第九周学习总结

20172310 2017-2018《程序设计与数据结构》（下）第九周学习总结

教材学习内容总结

这一章又要学习一个新的体系了——图

无向图、有向图和网络

接下来的例子都是使用这两个图

一些共同的基础概念：

  • 顶点：结点，一般用名字和标签来表示，如A、B等。

  • 边：节点之间的连接，用结点对来表示，如A、B顶点间的一条边（A，B）。

  • 邻接：如果图中的两个顶点之间有一条连通边，则称这两个顶点是邻接的，如图中AB邻接，A、D不邻接。

  • 自循环 ：连通一个顶点及其自身的边称为自循环或环, 例如，边(A,A) 表示的是连接A到自身的一个环。

  • 路径： 无向图中是指图中的一系列边，每条边连通两个顶点。例如，图1，ABD就是一条从A到D的路径。有向图中的路径是图中连通两个顶点的有向边序列。

无向图中的路径是双向的。例如，ABD确实是从A到D的路径，但由于这些边并没有方向，因此反过来，DBA又是从D到A的路径。

  • 路径的长度：是该路径中边的条数(或者是顶点数减去1)。如，从A到D的路径长度是2。注意， 这里对路径长度的定义等同于讨论树时用到的路径长度定义，因为， 树也是图的一种。

  • 环路：是一种首顶点和末顶点相同且没有重边的路径。在图1中，我们称路径ABCA是一条环路。没有环路的图称为无环的。

  • 连通：在无向图中，如果其中的任意两个顶点之间都存在一条路径，则认为这个无向图是连通的(connected)，连通有向图的定义听起来和连通无向图的定义一样。如果有向图中的任意两个顶点之间都存在一条路径， 则认为该有向图是连通的。但是记住，对有向图和无向图的路径定义是不同的。

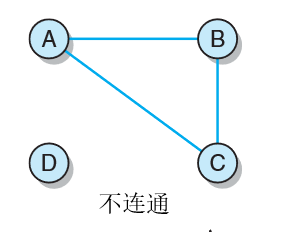
无向图：

  • 定义：无向图(undirected graph)是一种边为无序结点对的图。记作(A, B)的边就意味着A与B之间有一条从两个 方向都可以游历的连接 ，(A,B) 和记作(B,A) 的含义是完全样的。

  • 如果无向图拥有最大数目的连通顶点的边，则认为这个无向图是完全的。也就是说，对于第一个顶点，需要(n一1)条边将其与其他顶点连通。对于第2个顶点，只需(n-2)条边(除去与第一个顶点相连的边)。第三个顶点需要 (n-3)条边。 所以，对有n个顶点的无向图，要使该图为完全的，要求有n(n- 1)/2条边。注意，这里假设其中没有边是自循环的。

  • 无向树(undirected tree)是一种连通的无环无向图，其中一个元素被指定为树根。

有向图

  • 有向图(directed graph)有时也称为双向图(digraph),它是一种边为有序顶点对的图。这意味着边(A,B) 和边(B, A)在有向图中是不同的有向边。

  • 如果有向图中没有环路，且有一条从A到B的边，则可以把顶点A安排在顶点B之前。这种排列得到的顶点次序称为拓扑序(lopological order)

  • 有向树是种指定了个元素作为树根的有向图，还有如下属性:

    • 不存在其他顶点到树根的连接。

    • 每个非树根元素恰好有一个连接。

    • 树根到每个其他顶点都有一条路径。

网络

  • 网络(network),或称为加权图(weighted graph),是一种每 条边都带有权重或代价的图。网络可以是无向的，也可以是有向的，满足有向图或无向图的性质。通常，我们用一个三元组来表示每条边。，这个三元组中包括起始顶点、 终止项点和权重。记住，对无向网络来说，起始顶点与终止顶点可以互换。但对有向图来说，必须包含每个有向连接的三元组。

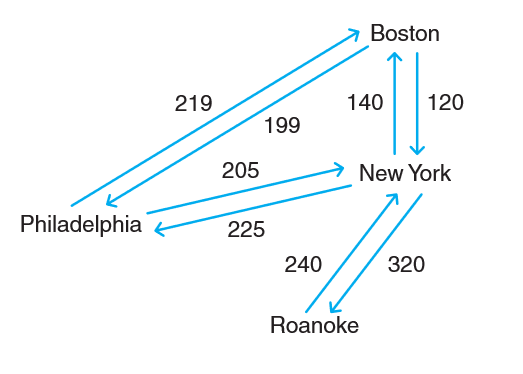
（这是一个网络，该网络描绘了在美国城市之间的连通性和飞机票价。这个加权图(或网络)可以用于确定从个城市到另一个城市的最便宜行程。）

  • 加权图中的路径权重是该路径中各条边权重的和。

图的常用算法

在这里我们学习的算法包括:各种遍历算法(这些遍历类似于探讨过的树遍历)，寻找最短路径的算法，寻找网络中最低代价路径的算法，回答一些简单图相关问题(例如，图是否是连通的，图中两个顶点间的最短路径是什么，等等)的算法。

遍历

  • 图的遍历分成两类（注意，图中不存在根结点，因此图的遍历可以从其中的任顶点开始）:
    • 广度优先遍历(breadth-first traversal),类似于树的层次遍历。

课本中用一个队列和一个无序列表来构造图的广度优先遍历。我们将使用队列(traversalQueue)来管理遍历，使用无序列表(resultList) 来构造出结果。
用一个实例来说明：


(1)往traversalQucue中添加9，并且把它标记为visited.
(2)从traversalQucuc中取出9.
(3)往resultList中添加9.
(4)往traversalQucue中添加6、7和8，网时把它们逐 标记为visited.
(5)从traversalQueuc中取出6。
(6)往resultList中添加6。
(7)往raversalQucue中添加3、4,同时把这两个顶点标记为vsited.
(8)从traversalQueue中取出7,并将它添加到resutList中。
(9)往traversalQueue中添加5,并且把它标记为visited.
(10)从traversalQueure中取出8，并将它添加到resutList中(这时不再往traversal.Qucue中添加任何新的顶点，因为顶点8再也没有尚未访问过的邻居了).
(11)从traversalQueuc中取出3，并将它添加到resultList中。
(12)往traversalQueue中添加1,并且把它标记为visited.
(13)从traversalQueue中取出4,并将它添加到resultList中。
(14)往traversalQueue中添加2，并且把它标记为visited.
(15)从traversalQueue中取出5,并将它添加到resultList中(由于再也没有未访问过的邻居，因此不需再往traversalQueue中添加顶点)。
(16)从traversalQueue中取出1,并将它添加到resultList中(由于再也没有未访问过的邻居，因此不需再往traversalQueue中添加顶点)。
(17)从traversalQucue中取出2，并将它添加到resultList中。
这样，resultList 就以广度优先次序存放了从顶点9开始的如下顶点: 9、6、7、8、3、4、5、1和2。

  • 深度优先遍历(depth-first traversal),类似于树的前序遍历。

图的深度优先遍历构造使用了同样的逻辑，只不过在深度优先遍历中用traversalStack代替了traversalQueue但是， 算法中还有一处不同：在顶点尚未添加到resultList之前，我们并不想标记该项点为visited.

测试连通性

  • 关键思想：不论哪个为起始顶点，当且仅当广度优先遍历中的顶点数目等于图中的顶点数目时，该图才是连通的。

最小生成树

  • 生成树(spanningtree)是一棵含有图中所有顶点和部分边(但可能不是所有边)的树。

  • 最小生成树(minimum spanningtree, MST)是加权图的最小生成树，它是一棵生成树， 其边的权重总和小于或等于同一个图中其他任何一棵生成树的权重总和。

  • 算法：任意选取个起始顶点(不管是哪一个)， 并将它添加到最小生成树中。然后，将所有含该起始顶点的边按照权重次序添加到minheap (最小堆)中。（如果处理的是有向网络，则只会添加那些以这个特定顶点为起点的边。）接着从minheap中取出最小边，并将这条边和那个新顶点添加到最小生成树中。下一步，我们往minbeap中添加所有含该新顶点的另一顶点尚不在最小生成树中的边。继续这过程，直到最小生成树含有原始图中的所有顶点(或minheap为空)时结束。

判定最短路径

  • 判定图的“最短”路径有两种情况。
    • 第一种， 判定起始顶点与目标顶点之间的字面意义上的最短路径，也就是两个顶点之间的最小边数。可以将广度优先遍历算法转变成寻找最短路径的算法，只需在遍历期间再对每个顶点存储另两个信息即可:从起始顶点到本顶点的路径长度，以及路径中作为本项点前驱的那个顶点。接着要修改循环，使得当抵达目标顶点时循环将终止。最短路径的路径长度就是从起始顶点到目标顶点前驱的路径长度再加1;如果要输出这条最短路径上的顶点，只需沿着前驱链回溯即可。
    • 判定最短路径的第二种情况是，寻找加权图的最便宜路径。用一个minheap或优先队列来存储顶点，基于总权重(从起始顶点到本顶点的权重和)来衡量顶点对，这样我们总是能优先沿着最便宜的路径来游历图。对每个顶点都必须存储该顶点的标签，(迄今为止)从起始顶点到本顶点的最便宜路径的权重，路径上本顶点的前驱。在minheap中将存储顶点、对每条已经遇到但尚未游历的候选路径来权衡顶点对。从minheap取出顶点的时候，会权衡取自minheap 的顶点对:如果遇到一个顶点的权重小于目前本顶点中已存储的权重，则会更新路径的代价。

图的实现策略

  • 邻接列表：对图结点来说，由于每个结点可以有多达n-1条边与其他结点相连，因此最好用种类似于链表的动态结点来存储每个结点带有的边。这种链表称为邻接列表(adjacency is)。对网络或加权图而言，每条边会存储成一个含权重的三元组。对无向图而言，边(A,B)会同时出现在顶点A和顶点B的邻接列表中。

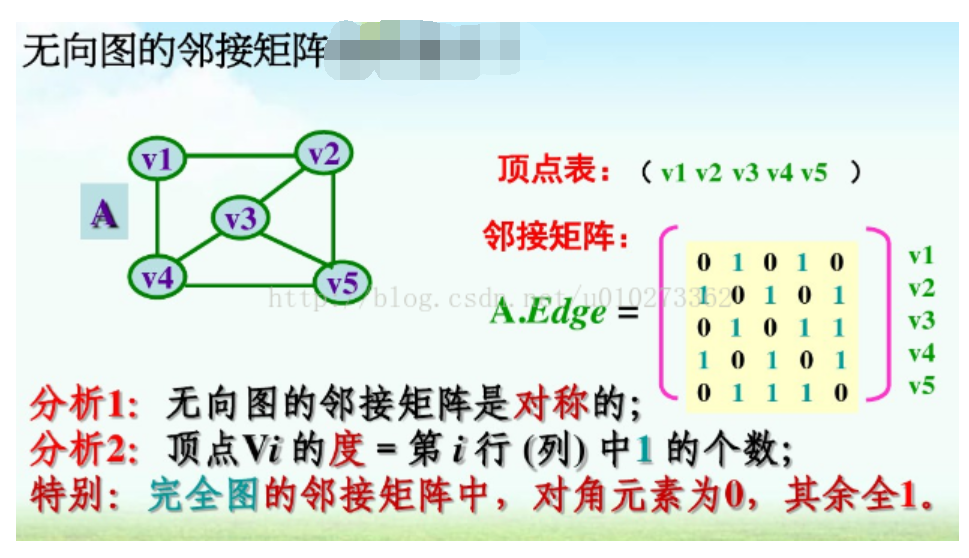
  • 邻接矩阵：邻接矩阵(adjacency matrix) 是一个二维数组。在邻接矩阵中，这个二维数组中的每个单元都表示了图中两个顶点的交接情况。对矩阵中的任何单元(row, colum)而言，当且仅当图中存在(Vrow,Vcolum)时,这个单元才为true。由于无向图中的边是双向的，因此，如果(A, B)是图中的一条边，那么(B,A)同样也是图中的一条边。

、
（注意，这个矩阵是对称的，即该矩阵对角线的一侧是另一 侧的镜像。 其原因就在于它所表示的是个无向图。 对无向图来说，没有必要表示整个矩阵，只需给出矩阵对角线的一侧(或另一侧)即可。）

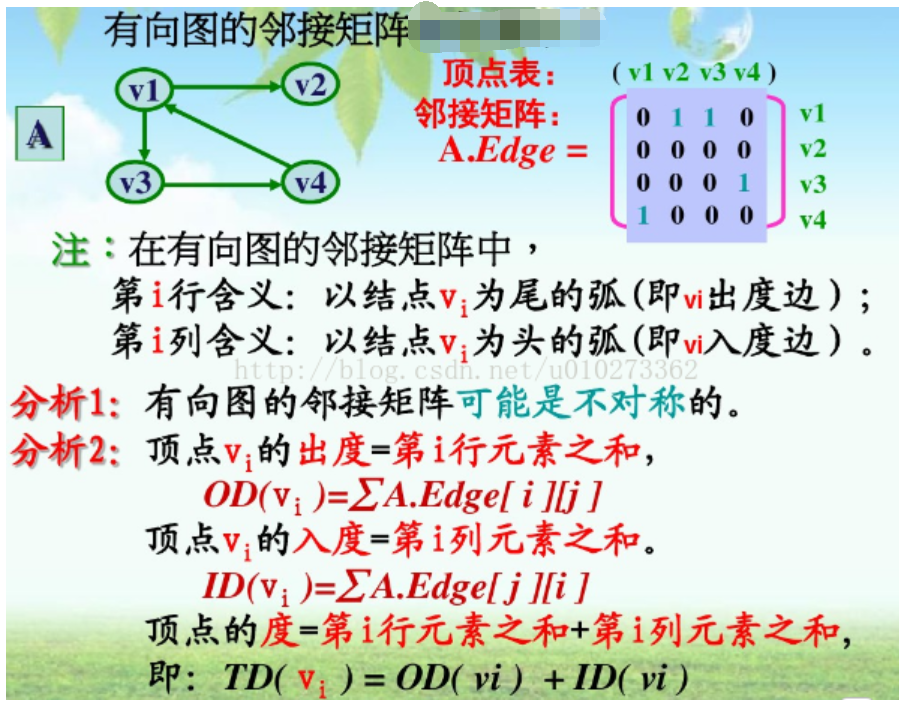
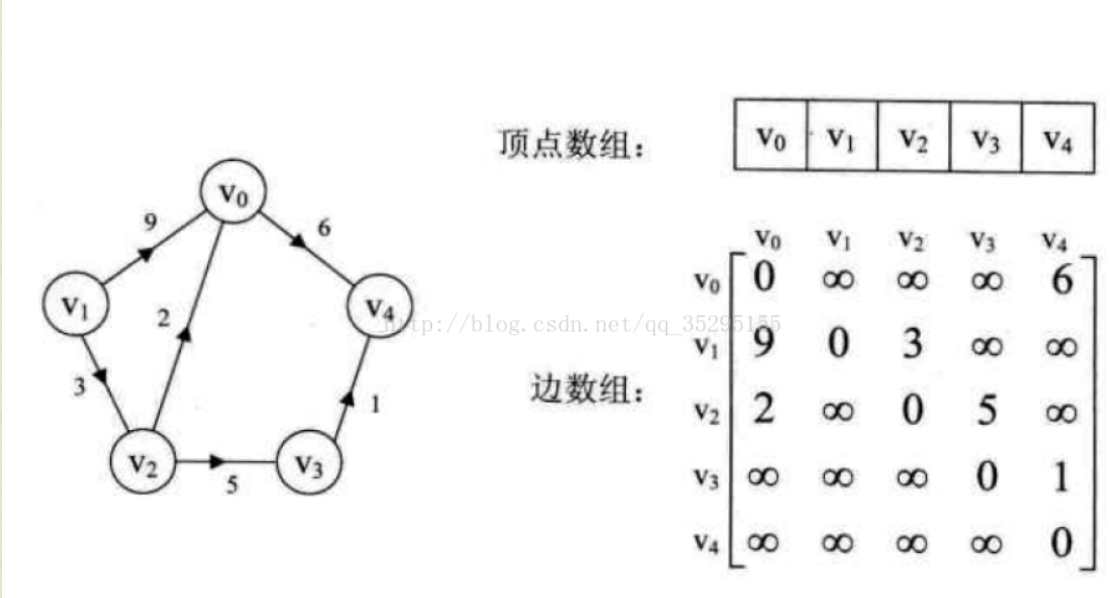
用邻接矩阵实现无向图

点击查看代码实现

教材学习中的问题和解决过程

  • 问题1：教材中讲述遍历的时候只详细介绍了广度优先遍历，和给出了深度优先遍历的代码，那深度优先遍历的情况是怎样的呢？而且遍历都是以无向图来说明的，但是如果有向图又该是什么样的情况呢？

  • 问题1解决方案：

  • 广度优先遍历在上面的教材总结中已经详细的介绍过一下流程

  • 深度优先遍历的情况

有向图的遍历其实就是看图是否是连通的，看网上的这幅图

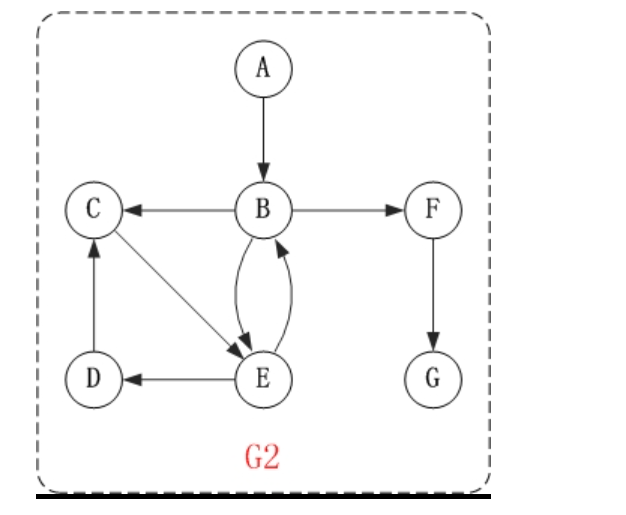
他的深度优先遍历情况就应该是：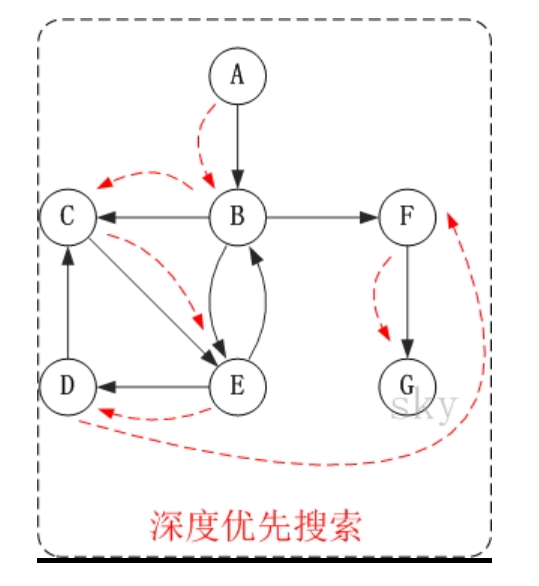

第1步：访问A。
第2步：访问B。
在访问了A之后，接下来应该访问的是A的出边的另一个顶点，即顶点B。
第3步：访问C。
在访问了B之后，接下来应该访问的是B的出边的另一个顶点，即顶点C,E,F。在本文实现的图中，顶点ABCDEFG按照顺序存储，因此先访问C。
第4步：访问E。
接下来访问C的出边的另一个顶点，即顶点E。
第5步：访问D。
接下来访问E的出边的另一个顶点，即顶点B,D。顶点B已经被访问过，因此访问顶点D。
第6步：访问F。
接下应该回溯"访问A的出边的另一个顶点F"。
第7步：访问G。
因此访问顺序是：A -> B -> C -> E -> D -> F -> G

他的广度优先遍历情况就应该是：

第1步：访问A。
第2步：访问B。
第3步：依次访问C,E,F。
在访问了B之后，接下来访问B的出边的另一个顶点，即C,E,F。前面已经说过，在本文实现中，顶点ABCDEFG按照顺序存储的，因此会先访问C，再依次访问E,F。
第4步：依次访问D,G。
在访问完C,E,F之后，再依次访问它们的出边的另一个顶点。还是按照C,E,F的顺序访问，C的已经全部访问过了，那么就只剩下E,F；先访问E的邻接点D，再访问F的邻接点G。
因此访问顺序是：A -> B -> C -> E -> F -> D -> G

大家也可以參考一下这篇资料图的遍历之 深度优先搜索和广度优先搜索

代码调试中的问题和解决过程

  • 问题1：编写pp15.1即用邻接列表实现无向图最难的在我看来是遍历的书写。

  • 问题1解决方案：之前我找百度，看见里面的写法很多都是直接调用了Java类库中的ArrayList类，我也找同学帮助看了看他们编写的思路，也有用了类库的那样他们的遍历方法可以继续使用原来的不用重新编写，但是我觉得那个本质上使用的只是数组套数组，并没有链表的影子。我还看到了另一种写法，就是使用自己当初编写的指针类，像是这样的。

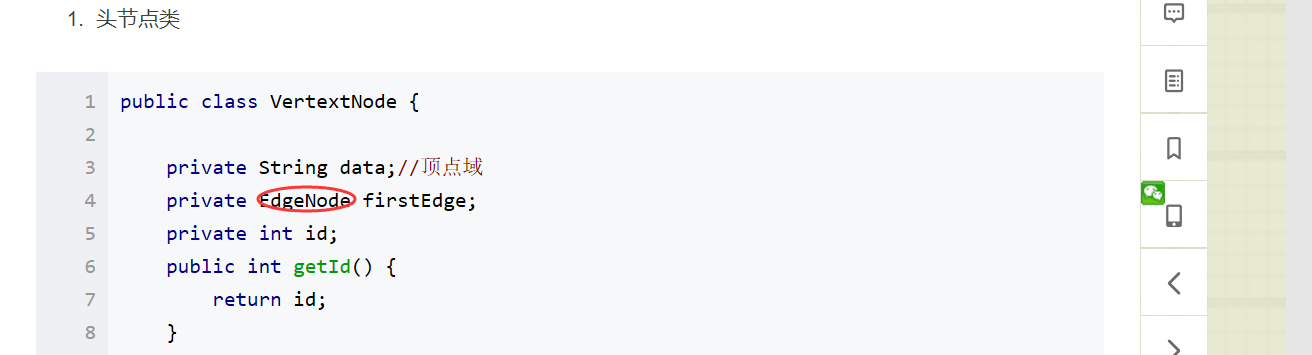
所以我想直接使用我们当初编写的LinearNode类，这样就像我们之前学习到的哈希函数的编写方法，但是这时的遍历方法就要改写。
对原来的代码进行了改写代码链接

  • 问题2：

  • 问题2解决方案：最近的的调试总是出现这样的问题，看样子是要解决一下了

（我之前还以为是当初的那个代码写的有问题，现在才发现看样子是有哪里出问题了，不然以后都调试不了了）

其实我的编写思路是和馨雨同学一样的，和她一样在写添加边的过程中出现了越界的问题，我思考了很久都没有想出是为什么（我觉得自己的思路没有问题TAT），然后就去参考了一些同学们的写法，最后屈服了，换了一种写法。

代码托管

上周考试错题总结

  • 错题1及原因，理解情况

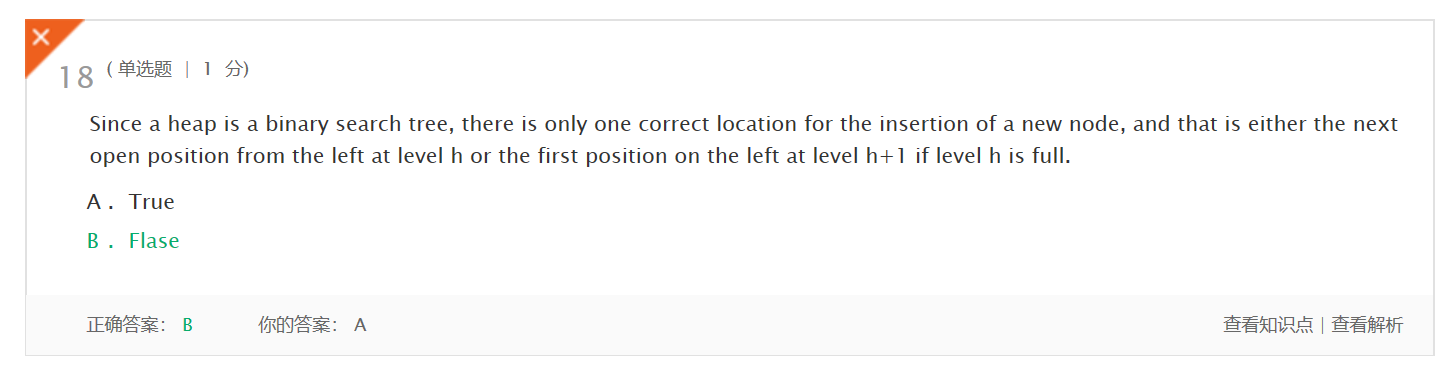
“因为堆是二叉搜索树，所以只有一个正确的位置用于插入新节点，并且如果级别h已满，该位置可以是从级别h左侧的下一个打开位置或在级别h+1左侧的第一个打开位置。”
这道题会错是因为自己只注意到了后面的讲述是对的，没看到最关键的前提 堆是一棵完全树，才有后面的内容。

结对及互评

点评：

  • 本周结对学习情况

  • 博客和代码中值得学习的或问题：

    • 教材和代码问题的总结很好。那些算法我都只是进行了粗略的理解，不像队友一样认真的总结了，值得学习。
    • 代码问题遇到了也都相应的进行了解决，而不是像我解决不了这个问题，就只好换一个写法，要多像队友讨教编写的思维，多多地练习。

点评过的同学博客和代码

其他（感悟、思考等，可选）

又是紧张的一周学习，其实这周的作业是上次作业都还没完成的情况下就发布了的，但还是时间紧张呀。这周其实课本
上给出的代码不算多，所以代码作业就看起来挺多的。时光匆匆，貌似我们这一本课本也学习完了（其实还是没有吃透(つД`)），
马上又要开始魔鬼般的实验作业了，希望我不会给我的小伙伴们拖后腿了。

学习进度条

|| | 代码行数（新增/累积）| 博客量（新增/累积）|学习时间（新增/累积）|重要成长|
| -------- | :----------------😐:----------------😐:---------------: |:-----😐
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 10/10 | |
| 第二周 | 326/326 | 1/2 | 18/28 | |
| 第三周 | 784/1110 | 1/3 | 25/53 | |
| 第四周 | 2529/3638 | 2/5 | 37/90 | |
| 第五周 | 1254/4892 | 2/7 | 20/110 | |
| 第六周 | 1403/6295 | 2/9 | 32/142 | |
| 第七周 | 1361/7656 | 1/10 | 35/177 | |
| 第八周 | 2750/10406 | 2/12 | 32/209 | |
| 第九周 | 2444/12850 | 1/13 | 23/232 | |

  • 计划学习时间:25小时

  • 实际学习时间:23小时

参考资料

posted @ 2018-11-18 16:54  qx2017  阅读(195)  评论(2)  编辑  收藏  举报
页尾