1 2 3 4

20172310 2017-2018《程序设计与数据结构》（下）第六周学习总结

20172310 2017-2018《程序设计与数据结构》（下）第六周学习总结

教材学习内容总结

非线性集合与数据结构，树的使用和实现。

概述（树的一些基本概念）

  • 树(tree)是一种非线性结构,其中元素被组织成了一个层次结构。
  • 树由一个包含结点(node)和边(edge)的集构成。元素被存储在这些结点中,边将一个结点和另一个结点连接起来。
  • 每一结点都位于该树层次结构中的某一特定层上。树的根(root)就是那个位于该树顶层的唯一结点。
  • 位于树中较低层的结点是上一层结点的孩子( children)。
  • 一个结点只有一个双亲,但是一个结点可以有多个孩子。同一双亲的两个结点称为兄弟( sibling)。根结点是树中唯一一个没有双亲的结点。没有任何孩子的结点称为叶子(leaf)。一个至少有一个孩子的非根结点称为一个内部结点( internal node)。
  • 树的类比是上下倒置的。
  • 根是树结构的进入点。我们可以沿着一条通过该树的路径从双亲到达孩子。
  • 假如A在从根开始的路径中位于另一结点B之上,则A就是B 的祖先( ancestor)。根是树中所有结点的最终祖先。沿着起始自某一特定结点的路径可以到达的结点是该结点的子孙( descendant)。
  • 结点的层也就是从根结点到该结点的路径长度。通过计算从根到该结点所必须越过的边数目,就可以确定其路径长度( path length)。根是位于层0的。
  • 树的高度( height)是指从根到叶子之间最远路径的长度。

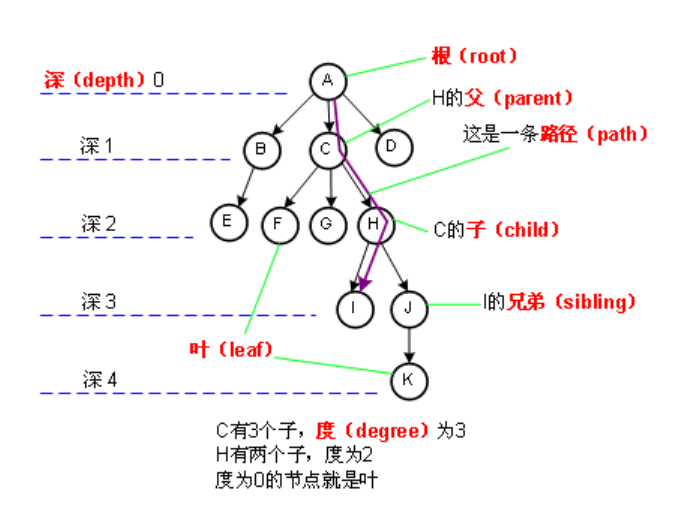
树的分类

  • n元树：：

    • 树中任一结点可以具有的最大孩子数目，这个值有时候也称为该树的度( order)。对结点所含有的孩子数目无限制的树称为广义树( general tree)。我们将每一结点限制为不超过n个孩子的树称为一棵n元树( n-ary tree)。
    • 结点最多具有两个孩子的树称为二叉树( binary tree)。

      平均二叉树的高度要比N小得多。分析表明，这个平均高度为O(√N)，而对于二叉查找树(binary search tree)，其高度的平均值是O(log N)。

  • 平衡树：

    • 如果树的所有叶子都位于同一层或者至少是彼此相差不超过一个层,就称之为是平衡的。

  • 完全树和满树：

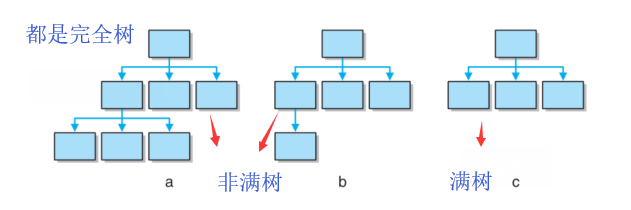
    • 在树是平衡树的基础上，底层所有叶子都位于树的左边,则认为该树是完全的。如果一棵n元树的所有叶子都位于同一层且每个结点要么是一片叶子要么正好具有n个孩子,则称此树是满的。

实现树的策略

  • 树的数组实现之计算策略
    ：一种可能的计算策略是将元素n的左孩子置于位置(2×n+1),将右孩子置于位置(2×(n+1)）（特别是对二叉树的实现）
    但有些缺陷：如果我们存储的树不是完全的或只是相对完全的,则该数组会为不包含数据的树位置分配空间,这就浪费了大量的存储空间。

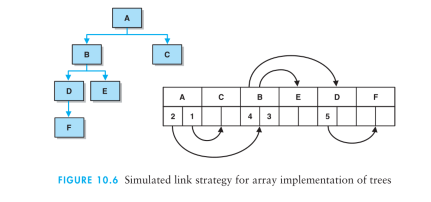
  • 树的数组实现之模拟链接策略
    ：第二个可能策略模拟了操作系统管理内存的方式。允许连续分配数组位置而不用考虑该树的完全性，该数组的每一元素都是一个结点类,每一结点存储的将是每一孩子(可能还有其双亲)的数组索引,而不是作为指向其孩子(可能还有其双亲)指针的对象引用变量。
    缺陷：增加了删除树中元素的成本,因为它要么需要对剩余元素进行移位以维
    持连续状态,要么需要保留一个空闲列表。

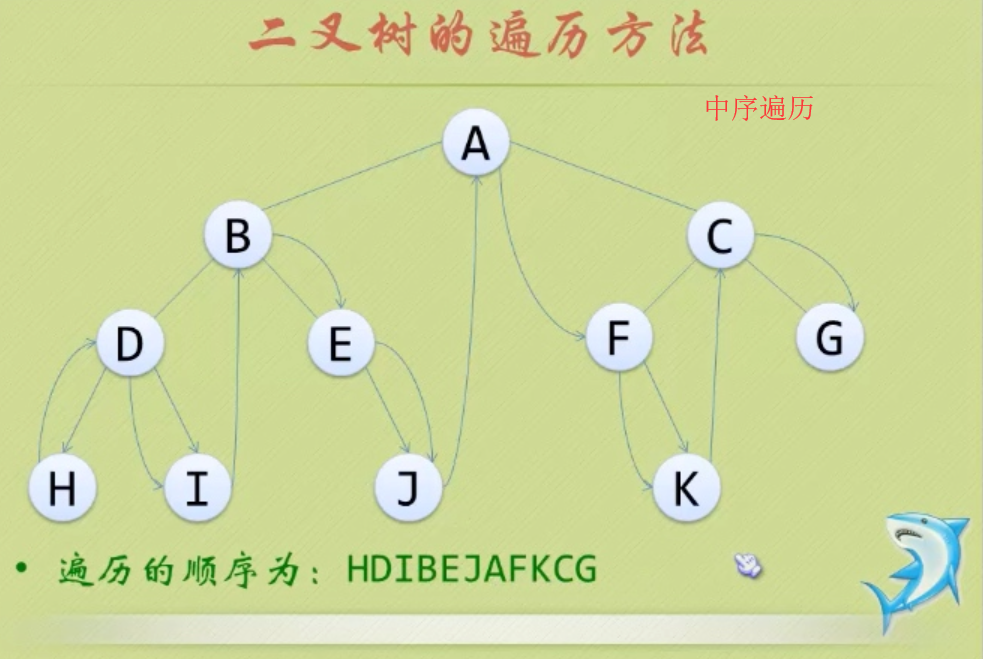
树的遍历

遍历一棵树有4种基本方法:




二叉树

  • 二叉树性质

    • 性质1：在二叉树的第i层上至多有2^i-1个结点（i>=1）。
    • 性质2：深度为k的二叉树至多有2^k-1个结点（k>=1）。
    • 性质3：对任何一颗二叉树T，如果其叶结点数为n0,度为2的 结点 数为n2，则n0 = n2+1。

  • 两种特殊的二叉树(1)

    • 满二叉树( Full Binary Tree ) :每层都“充满”了结点。深度为k，结点总数2k-1，每层结点数2i-1

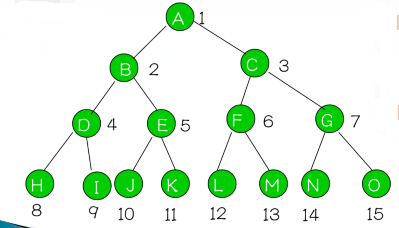
    • 完全二叉树( Complete Binary Tree )：树中所含的n个结点和满二叉树中编号为1至n的结点一一对应。（满二叉树去掉最下层最右边若干结点）

  • 完全二叉树的性质

    • 性质1：具有n个结点的完全二叉树深度为[log2n]+1 ([log2n]表示不 大于log2n的最大整数)。
    • 性质2：如果对一颗有n个结点的完全二叉树（其深度为[log2n]+1） 的结点按层序编号（从第1层到第[log2n]+1层，每层从左到右），对任意一个结点i(1<=i<=n)有：

  • 对二叉树的一些操作：

教材学习中的问题和解决过程

  • 问题1：树的高度和深度的区别？老师上课时重复提到了这两个概念，计算中很容易混淆这两个概念，那这两个概念到底是什么呢？
  • 问题1解决方案：

高度的定义课本给出的是指从根到叶子之间最远路径的长度。还有的说法是从结点x向下到某个叶结点最长简单路径中边的条数

就像是拿楼房来说，假如一个人提问：楼房的高度有多高？我们会从底层开始往上数，假如楼有6层，则我们会说，这个楼有6层楼那么高。
课本上的例子A到F有四层，但是却说他的高度为3。

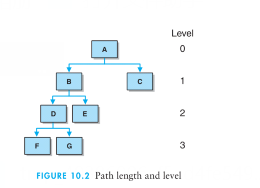
我在网上看了一些别的例子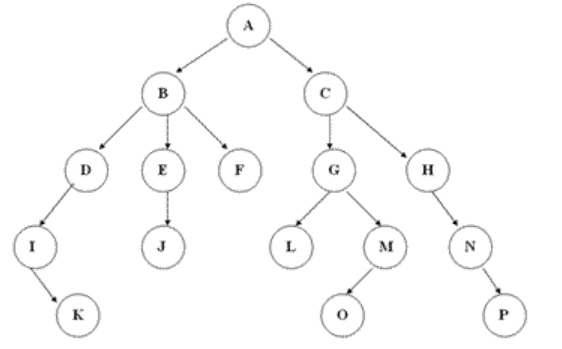
人家给出的A到K的高度却为5。

所以我理解其实高度这个主要是由于其根是1层还是0层产生了不同，但很多时候按习惯来说一般都是以1开始。

深度是从根节点往下，深度是从根节点开始（其深度为1）自顶向下逐层累加的。

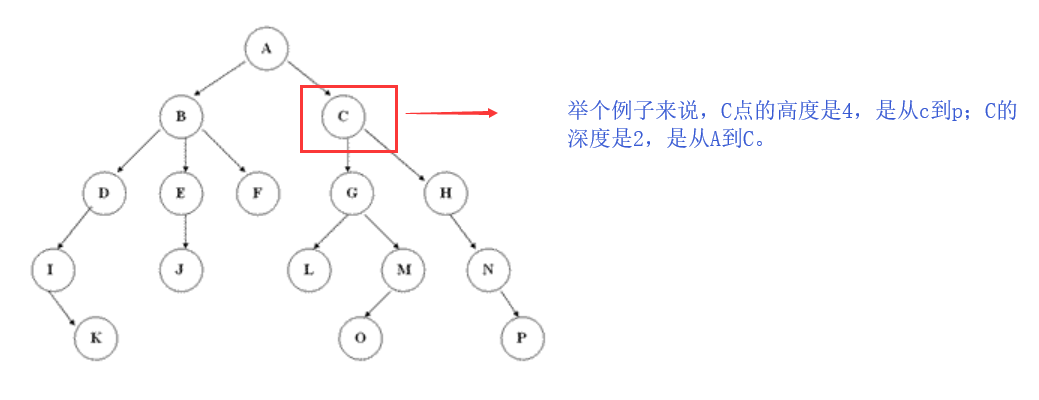
总的来说对于整棵树来说，最深的叶结点的深度就是树的深度；树根的高度就是树的高度。这样树的高度和深度是相等的。
对于树中相同深度的每个结点来说，它们的高度不一定相同，这取决于每个结点下面的叶结点的深度。

  • 问题2：书中代码的理解
  public int evaluateNode(BinaryTreeNode root)
    {
        int result, operand1, operand2;
        ExpressionTreeOp temp;

        if (root==null)
            result = 0;
        else
        {
            temp = (ExpressionTreeOp)root.getElement();

            if (temp.isOperator())//判断temp是否是一个操作符，如果是一个操作数，进入循环，递归
            {
                operand1 = evaluateNode(root.getLeft());
                operand2 = evaluateNode(root.getRight());
                result = computeTerm(temp.getOperator(), operand1, operand2);
            }
            else//如果是操作符，则返回值
                result = temp.getValue();
        }

        return result;
    }
  • 问题2的解决方案：isOperator()方法是写在ExpressionTreeOp类中
 public boolean isOperator() 
    {
        return (termType == 1);
    }

相应的解释就在代码后加入了自己的理解。

代码调试中的问题和解决过程

  • 问题1：
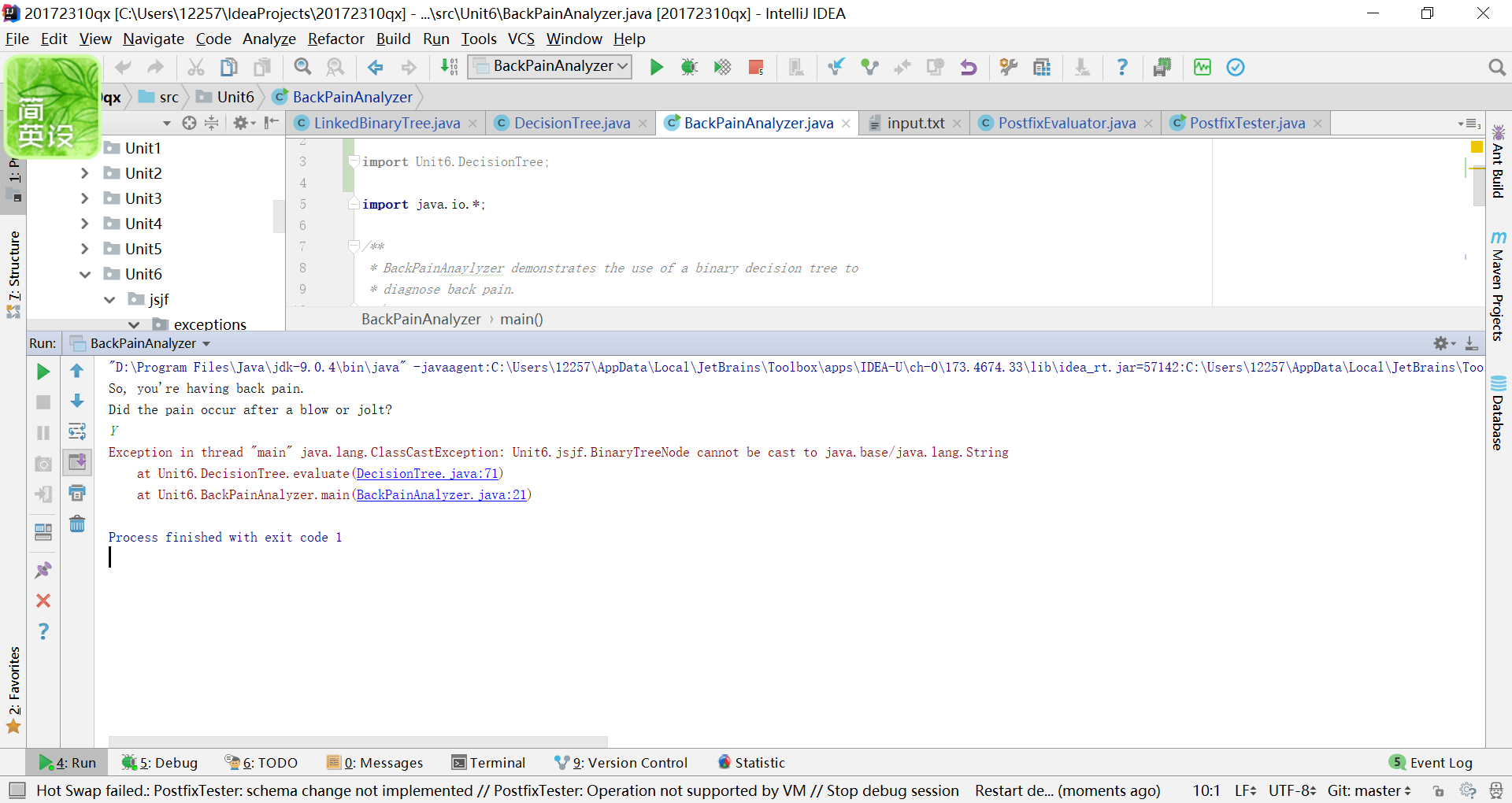
    给出的信息是在循环出出现了错误，但是循环的代码并没用问题。就跟在打印二叉树的表达树时，也出现了错误

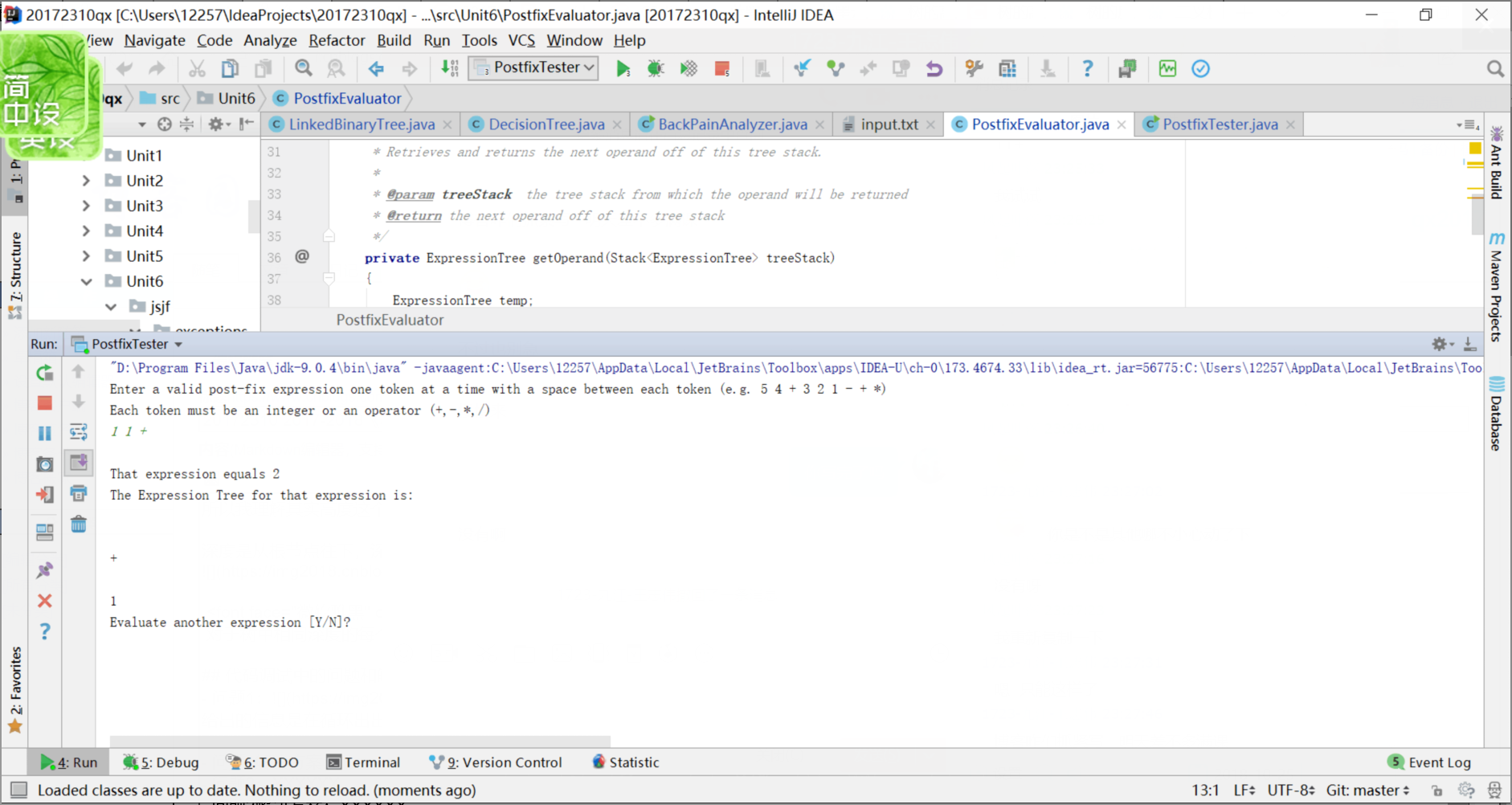
是最根本的LinkedBinaryTree.java文件中的方法发生了错误，于是进行了调试

发现GetRight和GetLeft的返回值是错误的，继续发现原来是没有编写成功height()方法。

  • 问题1解决方案：于是就进行了如下的更改。

最后得出了正确的显示

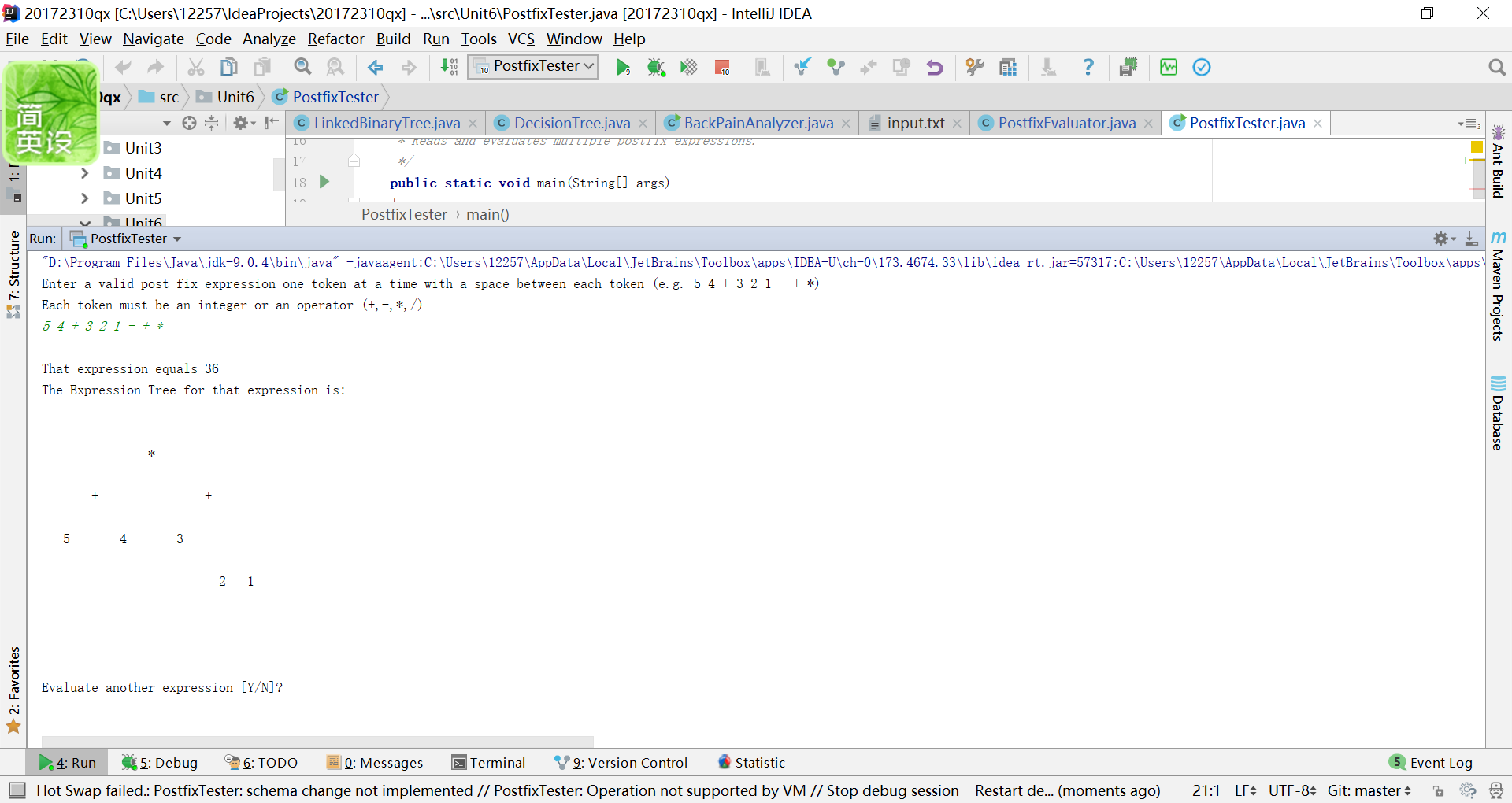
代码托管

上周考试错题总结

上周已总结。

结对及互评

点评：

  • 本周结对学习情况
  • 博客和代码中值得学习的或问题：
  • 教材中的问题总结的很详细，第一个问题，因为课本上都是用的二叉树为例子，但是

那么当一个节点只有一个孩子的时候，此时没有左右孩子之分。

我觉得就算没有两个或以上的孩子，但也能根据位置来确定相对的左右。图的画法好像有点错。此外，结果好像也有点问题，如果它不是左孩子，那么会先访问该节点，所以我认为答案是D、H、B、E、A、F、C、G。

格式好像有点问题。

  • 对课本教材的代码理解很好。

点评过的同学博客和代码

其他（感悟、思考等，可选）

第十章内容真的是又多又难呀，树是新接触的概念，其中有很多的细小的知识和概念要去理解，在总结和记忆这些小知识点上花的时间还是很多的。此外，这章的代码其实很难理解，我们上个学期学了迭代，但说句实话，内容都有些忘了，而且这章不仅使用了迭代，而且代码的逻辑，代码为什么这样写都有些难以理解，书上的代码有些都因为时间限制，就先囫囵吞枣了一番，之后才慢慢理解了。

学习进度条

|| | 代码行数（新增/累积）| 博客量（新增/累积）|学习时间（新增/累积）|重要成长|
| -------- | :----------------😐:----------------😐:---------------: |:-----😐
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 10/10 | |
| 第二周 | 326/326 | 1/2 | 18/28 | |
| 第三周 | 784/1110 | 1/3 | 25/53 | |
| 第四周 | 2529/3638 | 2/5 | 37/90 | |
| 第五周 | 1254/4892 | 2/7 | 20/110 | |
| 第六周 | 1403/6295 | 2/9 | 32/142 | |

  • 计划学习时间:30小时

  • 实际学习时间:32小时

  • 改进情况：
    这周因为学习内容较多，所以时间也较长，但还是要提高一下学习的效率。

参考资料

posted @ 2018-10-25 20:43  qx2017  阅读(345)  评论(1)  编辑  收藏  举报
页尾