1 2 3 4

20172310 《程序设计与数据结构》（下）第一周学习总结

20172310 《程序设计与数据结构》（下）第一周学习总结

教材第一、二章学习内容总结

  • 第一章 概述

    • 软件质量：
      1、软件工程是一门关于高质量软件开发的技术和理论的学科
      2、高质量软件的特征

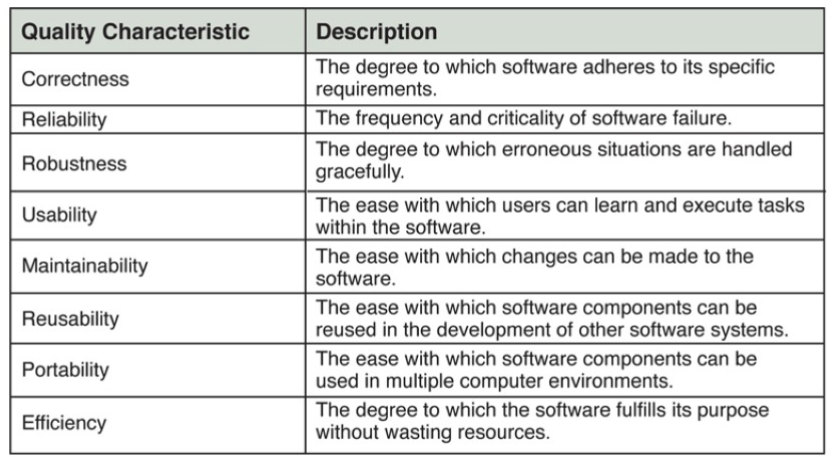
    • 数据结构：

  • 第二章 算法分析
    算法分析是计算机科学的基础。算法的效率是决定一个程序运行速度的主要因素。

    • 增长函数和大O记法：
      1、增长函数：表示与该问题大小相对应的时间或者空间的使用，表示问题（n）大小与我们希望最优化的值之间的关系。该函数表示了该算法的事件复杂度或空间复杂度。
      2、渐进复杂度：称为算法的阶次。如书，第二个洗盘子的算法具有阶次为n2的时间复杂度，记为O（n2），这种记法称为O()或者大O记法。渐进复杂度这一特性基于该表达式的主项。算法的阶次是忽略该算法的的增长函数中的常量和其他次要项，只保留主项而得出的。其中，与问题大小无关、执行时间恒定的增长函数具有O（1）的复杂度

3、算法的阶次为增长函数提供了一个上界。
- 增长函数的比较：
1、渐进复杂度为线性

注：其中里面3.16、2.15、3.3的算法为，√10≈3.162277660168379、³√10≈2.1544、log2(10)=lg(10)/lg(2)=1/lg(2)=3.321928
所以说，更快的CPU，并不能影响主项，只会给增长函数增加常量，仍需要重视算法分析，如果算法的运行效率低，那么从长远来看，再快的CPU也无济于事。
2、n值较小和n 值较大时各种增长函数的比较

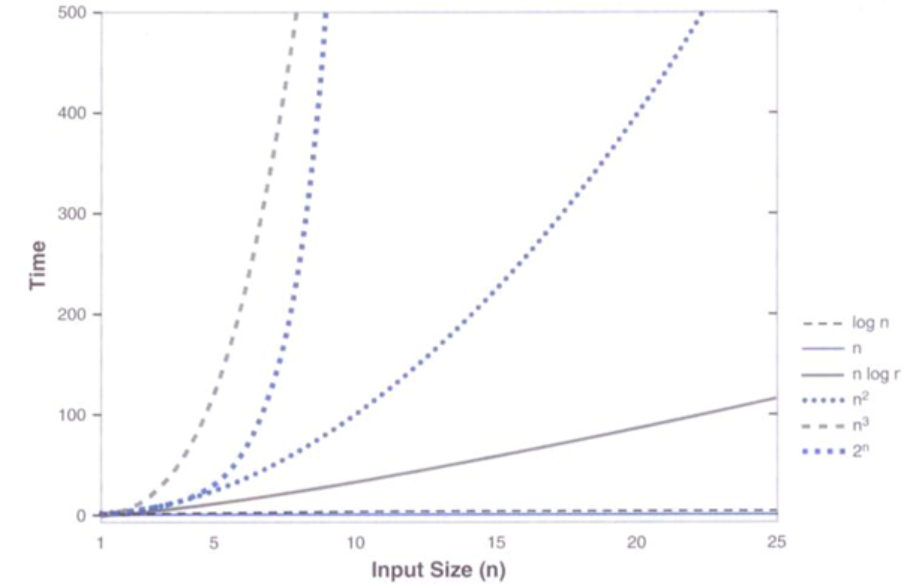
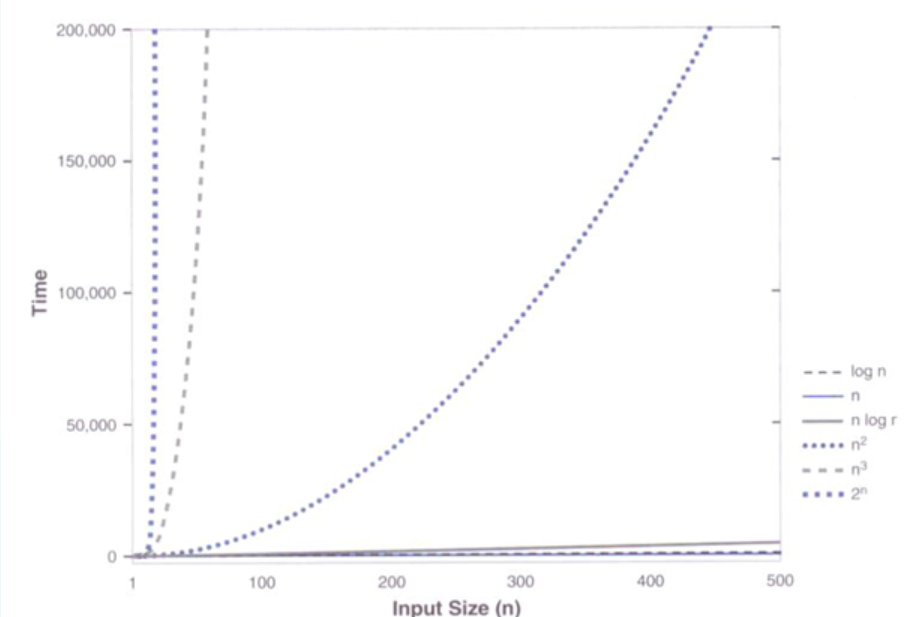
- 时间复杂度分析

1、循环运行的复杂度分析
要确定某个算法的阶次，常常需要确定某个特定语句或某个语句集运行的次数。要确定该循环的阶数n，然后要运行的次数乘以它，n表示问题的大小。

for(int count = 0;count<n;count++)
{
//*复杂度为O(1)的步骤系列
}

count = 1;
while(count < n)
{
count *=2;
//复杂度为O(1)的步骤系列
}

2、嵌套循环的复杂度分析
分析嵌套循环的复杂度是，必须jiang 内层循环的复杂度乘以外层循环都考虑进来。

for(int count = 0;count < n;count++)
{
   for(int count2 = 0;count2<n;count2++)
    {
        //复杂度为O(1)的步骤系列
    }
}

内层循环的复杂度根据上述的算法得到复杂度为O（n），再与外层循环次数相乘，得到嵌套循环的复杂度为O（n^2）。

3、方法调用的复杂度分析
考虑清楚调用方法的复杂度，在进行接下来的分析
如果调用多个方法或多次方法，最后可忽略常量和非主要项。

教材学习中的问题和解决过程

  • 问题1：高质量软件的几个特征中有几个性质比较难以区分，需要好好理解。

  • 问题1解决方案：

    • 可靠性和健壮性：可靠性是指可靠的软件很少发生故障，即使发生了故障，也可以将该故障的影响降到最低。健壮性而是指一个系统能够处理各种各样的问题的或反馈错误信息的能力
    • 可重用和可移植性：可重用是软件组件可以应用在另一个软件系统中，不需要从零开始。设计可移植性则是指Java的源代码被编译成了字节码，这是一种低级语言，他不是任何特定CPU的机器语言。字节码运行在Java虚拟上（JVM）。JVM是一种解释并执行字节码的软件。

  • 问题2：循环运行的复杂度分析中，课本上给出的两个例子的复杂度的分析

for(int count = 0;count<n;count++)
{
//*复杂度为O(1)的步骤系列
}

count = 1;
while(count < n)
{
count *=2;
//复杂度为O(1)的步骤系列
}
  • 问题2解决方案：要解决这个问题最重要的是不要混淆循环体的复杂度和循环运行的复杂度。这里两个循环体的复杂度其实是一样的，循环设计会跳过某个数，只要所跳过的部分是线性部分，循环体的复杂度仍是O（1）。
    其实课本上各处的复杂度分析的基础都是要先弄懂简单循环复杂度的分析，然后再慢慢地有里向外分析就好。

课后习题

  • EX 2.1：下列增长函数的阶次是多少？解题关键是忽略常量和非主要项
    a.10n^2+100n+1000
    解：阶次为：n^2。
    b.10n^3-7
    解：阶次为：n^3
    c.2n+100n3
    解：阶次为：n^3
    d.n^2 ·log(n)
    解：阶次：n^2 ·log(n)
  • EX 2.4：请确定下面代码段的增长函数和阶次
for(int count = 0 ; count < n ; count++)
    for(int count2 = 0 ; count2 < n ; count2 = count2 + 2)
        {
            System.out.println(count,count2);
        }
}

解：内层循环复杂度为O（n/2），外层循环需要进行的次数是n，故增长函数为F(n)=(n2)/2，阶次为n2

  • EX 2.5：请确定下面代码段的增长函数和阶次
for(int count = 0 ; count < n ; count++)
    for(int count2 = 1 ; count2 < n ; count2 = count2 * 2)
        {
            System.out.println(count,count2);
        }
}

解：内层循环进行的次数是O（log₂n），外层循环需要进行的次数是n，故增长函数为F(n)=n·log₂n，所以阶次为n·log2n。

结对及互评

点评的同学博客和代码

  • 本周结对学习情况
    • 20172309
    • 结对学习内容
      • 教材一二章学习

点评：

  • 博客中值得学习的或问题：
    • 教材内容总结详细，简洁明了地总结出重点内容，而不是照搬教材。
    • 教材问题的提出很有用，解答也很正确。

其他（感悟、思考等，可选）

这个学期的Java课又要开始了，我只想说，革命尚未成功，同志仍需努力，Java的学习道路还有很长，这个学期要更加努力啦٩(๑>◡<๑)۶

学习进度条

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 5000行 30篇 400小时
第一周 0/0 1/1 10/10

参考资料

posted @ 2018-09-09 22:55  qx2017  阅读(217)  评论(2)  编辑  收藏  举报
页尾