自适应滤波之RLS算法（含MATLAB+Python代码）

前言
LMS算法的主要优点在于它的计算简单，然而为此付出的代价是缓慢的收敛速度，特别是当自相关矩阵\(\pmb{\varGamma}_M\)的特征值具有较大范围时。从另一个观点来看，LMS算法只有单一的可调参数，即步长参数\(\Delta\)用于控制收敛速度。因为出于稳定的目的，步长是有限制的，所以应对与较小特征值方式的收敛速度较慢。为了较快的收敛，就需要设计出包含额外参数的更加复杂的算法。接下来即是将要介绍的RLS算法。
RLS算法
定义在\(n\)时刻的长度为\(M\)的滤波器系数向量为：

\[\begin{align} \pmb{h}_M(n) = \begin{bmatrix} h(0,n)\\ h(1,n)\\ h(2,n)\\ \vdots\\ h(M-1,n) \end{bmatrix} \end{align} \]

同样地，在\(n\)时刻的输入信号向量表示为：

\[\begin{align} \pmb{X}_M(n) = \begin{bmatrix} x(n)\\ x(n-1)\\ x(n-2)\\ \vdots\\ x(n-M+1) \end{bmatrix} \end{align} \]

当\(n<0\)时，\(x(n)=0\)。

递归最小二乘方问题现在可以描述为如下：假如我们观察到的向量为\(\pmb{X}_M(l),l=0,1\\,\cdots,n\)，此时将误差定义为期望序列\(d(l)\)和估计\(\hat{d(l,n)}\)之间的差值：

\[\begin{align} e_M(l,n) &= d(l) - \hat{d}(l,n) \nonumber \\ &=d(l) - \pmb{h}_M^t(n) \pmb{X}_M(l) \end{align} \]

而我们希望的是确定使误差幅度平方的加权和:

\[\begin{align} \xi_M = \sum_{l=0}^n w^{n-l}|e_M(l,n|^2 \end{align} \]

达到最小时的滤波器系数向量\(\pmb{h}_M(n)\)，其中\(w\)是范围为\(0<w<1\)的加权因子。使用加权因子的目的是加重最近数据点的权值，这样使得滤波器系数能够适应时变的数据统计特性，这可以通过对过去的数据使用指数加权因实现。

\(\xi_M\)关于滤波器系数向量\(\pmb{h}_M(n)\)的最小化可以产生出线性方程组（证明过程附在后面）

\[\begin{align} \pmb{R}_M(n)\pmb{h}_M(n) = \pmb{D}_M(n) \end{align} \]

其中，\(\pmb{R}_M(n)\)是信号自相关矩阵，定义为

\[\begin{align} \pmb{R}_M(n) = \sum_{l=0}^{n}w^{n-l}\pmb{X}_M^*(l)\pmb{X}_M^t(l) \end{align} \]

\(\pmb{D}_M(n)\)是互相关向量

\[\begin{align} \pmb{D}_M(n) = \sum_{i=0}^nw^{n-l}\pmb{X}_M^*(l)d(l) \end{align} \]

方程式（1.5）的解为

\[\begin{align} \pmb{h}_M(n) = \pmb{R}_M^{-1}(n) \pmb{D}_M(n) \end{align} \]

相比LMS中的自相关矩阵，\(\pmb{R}_M(n)\)不是Herimitian矩阵，而\(\pmb{\varGamma}_M\)是。对于小的\(n\)值，\(\pmb{R}_M(n)\)可能是病态的，因而它的逆是不可求的。在这种情况下，习惯在初始化时要将\(\pmb{R}_M(n)\)加上矩阵\(\delta\pmb{I}_M\)，其中，\(\pmb{I}_M\)是单位阵，\(\delta\)是小的正常数。给过去的数据加上指数加权，\(\delta\pmb{I}_M\)增加的影响就会随着时间消失。

首先\(\pmb{R}_M(n)\)的递归更新方程可以写为

\[\begin{align} \pmb{R}_M(n) = w\pmb{R}_M(n-1) + \pmb{X}_M^*(n)\pmb{X}_M^t(n) \end{align} \]

因为我们需要\(\pmb{R}_M(n)\)的逆，所以运用矩阵求逆定理，可以得到

\[\begin{align} \pmb{R}_M^{-1}(n) = \frac{1}{w} \left[\pmb{R}_M^{-1}(n-1)- \frac{\pmb{R}_M^{-1}(n-1)\pmb{X}_M^*(n)\pmb{X}_M^t(n)\pmb{R}_M^{-1}(n-1)} {w +\pmb{X}_M^t(n)\pmb{R}_M^{-1}(n-1)\pmb{X}_M^*(n) }\right] \end{align} \]

这样，\(\pmb{R}_M^{-1}(n)\)就可以递归的计算。

为了方便起见，定义\(\pmb{P}_M(n)=\pmb{R}_M^{-1}(n)\)，则式（8）可以重写为：

\[\begin{align} \pmb{h}_M(n) = \pmb{P}_M(n)\pmb{D}_M(n) \end{align} \]

还可以定义一个\(M\)维的向量\(\pmb{K}_M(n)\)，称其为卡尔曼增益向量，其形式为

\[\begin{align} \pmb{K}_M(n) &=\frac{\pmb{P}_M(n-1)\pmb{X}^*_M(n)}{w + \pmb{X}_M^t(n)\pmb{P}_M(n-1)\pmb{X}_M^*(n)} \nonumber \\ &= \frac{1}{w + \mu_M(n)}\pmb{P}_M(n-1)\pmb{X}^*_M(n) \end{align} \]

其中，\(\mu_M(n)\)是一个标量，定义为

\[\begin{align} \mu_M(n) = \pmb{X}_M^t(n)\pmb{P}_M(n-1)\pmb{X}_M^*(n) \end{align} \]

利用这些定义，式（10）就变为

\[\begin{align} \pmb{P}_M(n) = \frac{1}{w}\left[\pmb{P}_M(n-1)-\pmb{K}_M(n)\pmb{X}^t_M(n)\pmb{P}_M(n-1) \right] \end{align} \]

此时，我们在上式（1.14）右乘\(\pmb{X}_M^*(n)\)，就可以得到比较惊喜的结果

\[\begin{align} \pmb{P}_M(n)\pmb{X}_M^*(n) &= {\frac{1}{w}\left[\pmb{P}_M(n-1)\pmb{X}_M^*(n) - \pmb{K}_M(n)\pmb{X}^t_M(n)\pmb{P}_M(n-1)\pmb{X}_M^*(n) \right]} \nonumber\\ &=\frac{1}{w}\left\{[w + \mu_M(n)]\pmb{K}_M(n) -\pmb{K}_M(n)\mu_M(n) \right\}\nonumber\\ &= \pmb{K}_M(n) \end{align} \]

因此，卡尔曼增益向量也可以定义为\(\pmb{P}_M(n)\pmb{X}_M^*(n)\)。

将向量\(\pmb{D}_M(n)\)的递归更新方程可以写为

\[\begin{align} \pmb{D}_M(n) = w \pmb{D}_M(n-1) + d(n)\pmb{X}_M^*(n) \end{align} \]

现在将\(\pmb{D}_M(n)\)的更新方程(16)和 \(\pmb{P}_M(n)\)的更新方程(10)带入式(11)中，可以得到

\[\begin{align} \pmb{h}_M(n) &= \frac{1}{w}\left[\pmb{P}_M(n-1)-\pmb{K}_M(n)\pmb{X}^t_M(n)\pmb{P}_M(n-1) \right]\left[w \pmb{D}_M(n-1) + d(n)\pmb{X}_M^*(n)\right] \nonumber\\ &=\pmb{P}_M(n-1)\pmb{D}_M(n-1) + \frac{1}{w} d(n)\pmb{P}_M(n-1)\pmb{X}_M^*(n)\nonumber \\ & ~~~ -\pmb{K}_M(n)\pmb{X}^t_M(n)\pmb{P}_M(n-1)\pmb{D}_M(n-1) - \frac{1}{w}d(n)\pmb{K}_M(n)\pmb{X}^t_M(n)\pmb{P}_M(n-1)\pmb{X}_M^*(n)\nonumber\\ &= \pmb{h}_M(n-1)-\pmb{K}_M(n)\pmb{X}^t_M(n)\pmb{h}_M(n-1)+ \nonumber \\ & ~~~ d(n){\frac{1}{w} \left[\pmb{P}_M(n-1)\pmb{X}_M^*(n) - \pmb{K}_M(n)\pmb{X}^t_M(n)\pmb{P}_M(n-1)\pmb{X}_M^*(n)\right]} \nonumber\\ &=\pmb{h}_M(n-1) - \pmb{K}_M(n)\pmb{X}^t_M(n)\pmb{h}_M(n-1) + d(n)\pmb{K}_M(n) \nonumber \\ &=\pmb{h}_M(n-1) + \pmb{K}_M(n) \left[d(n) - \pmb{X}^t_M(n)\pmb{h}_M(n-1)\right] \end{align} \]

在上面的式子最后一项中，\(\pmb{X}^t_M(n)\pmb{h}_M(n-1)\)是自适应滤波在n时刻的输出，该值是基于n-1时刻的滤波器系数得到的。因为

\[\begin{align} \pmb{X}^t_M(n)\pmb{h}_M(n-1) = \hat{d}(n,n-1) \equiv \hat{d}(n) \end{align} \]

并且

\[\begin{align} e_M(n,n-1) = d(n) - \hat{d}(n,n-1) \equiv e_M(n) \end{align} \]

因此\(\pmb{h}_M(n)\)的更新方程可以表示为

\[\begin{align} \pmb{h}_M(n) = \pmb{h}_M(n-1) + \pmb{K}_M(n) e_M(n) \end{align} \]

或者等价于

\[\begin{align} \pmb{h}_M(n) = \pmb{h}_M(n-1) + \pmb{P}_M(n)\pmb{X}_M^*(n) e_M(n) \end{align} \]

附
证明：设

\[\begin{align} f(\pmb{x})&=|| \pmb{Ax}-\pmb{b}||_2^2=(\pmb{Ax}-\pmb{b})^T(\pmb{Ax}-\pmb{b})\nonumber\\ &=\pmb{x}^T\pmb{A}^T\pmb{A}\pmb{x}-\pmb{x}^T\pmb{A}^T\pmb{b}-\pmb{b}^T\pmb{A}\pmb{x}+\pmb{b} ^T\pmb{b}\end{align} \]

若\(\pmb{x}_0\)为\(\pmb{A}\pmb{x}=\pmb{b}\)的最小二乘解，则它应是\(f(\pmb{x})\)的极小点，从而

\[\frac{df}{d\pmb{x}}|_{\pmb{x}_{0}}=\pmb{0}. \]

对上式求导可得：

\[\frac{df}{d\pmb{x}}=2\pmb{A}^T\pmb{A}\pmb{x}-2\pmb{A}^T\pmb{b}. \]

最终得到方程组：

\[\pmb{A}^T\pmb{A}\pmb{x}=\pmb{A}^T\pmb{b}. \]

算法流程表

MATLAB代码

close all;clear all;clc;

%% 产生测试信号
fs = 1;
f0 = 0.02;
n = 1000;
t = (0:n-1)'/fs;
xs = cos(2*pi*f0*t);
SNR = 10;
ws = awgn(xs, SNR, 'measured');


%% main
w = 0.1;
delta = 2;
[d,error_vect,estimate_h] = RLS_func(w,xs,ws,delta);
figure
subplot(211)
plot(d)
grid on;ylabel('幅值');xlabel('时间');
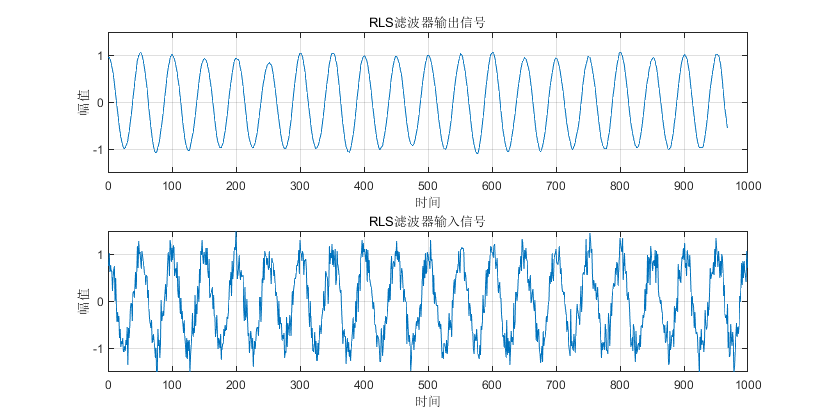
ylim([-1.5 1.5]);title('RLS滤波器输出信号');
subplot(212)
plot(ws)
grid on;ylabel('幅值');xlabel('时间');title('RLS滤波器输入信号');
ylim([-1.5 1.5]);


%% RLS函数
function [d,error_vect,estimate_h] = RLS_func(w,xs,ws,delta)
% 参数初始化
L = 32; %滤波器长度
n = 1000;
X_n = ws;
d_n = xs;
P_M = delta*eye(L,L);
estimate_h = zeros(L,1);
estimate_h(1,:) = 1;
error_vect = zeros(n-L,1);

    for i =1 : n-L
        x_vect = X_n(i:i+L-1);
        mu = x_vect.' * P_M * conj(x_vect);
        K = P_M * conj(x_vect) / (w + mu);
        P_M = (P_M - K * x_vect.' * P_M);
        estimate_d = x_vect.' * estimate_h;
        error = d_n(i) - estimate_d;
        error_vect(i,:) = error;
        estimate_h = estimate_h + K * error;
    end
    d = inf * ones(size(X_n));
    for i = 1:n-L
        x_vect = X_n(i:i+L-1);
        d(i)  = estimate_h.' * x_vect;
    end
end

简单实验结果：

Python实验代码

import numpy as np
import matplotlib.pyplot as plt


# 信号加噪
def awgn(x, snr):
    snr = 10 ** (snr / 10.0)
    xpower = np.sum(np.abs(x) ** 2) / len(x)
    npower = xpower / snr
    if type(x[0]) != np.complex128:
        return x + np.random.randn(len(x)) * np.sqrt(npower)
    else:
        return x + np.random.randn(len(x)) * np.sqrt(npower / 2) + 1j * np.random.randn(len(x)) * np.sqrt(npower / 2)


def RLS_func(w,xs,ws,delta,L):
    # L = 32    #滤波器长度
    n = 1000
    X_n = ws
    d_n = xs
    P_M = np.multiply(delta,np.identity(L))
    estimate_h = np.zeros(L)
    estimate_h[0] = 1
    error_vect = np.zeros(n-L)

    for i in range(0,n-L):
        x_vect = X_n[i:i+L]
        mu = np.dot(np.dot(np.transpose(x_vect),P_M),np.matrix.conjugate(x_vect))
        K = np.divide(np.dot(P_M,np.matrix.conjugate(x_vect)),(w+mu))
        P_M= np.subtract(P_M,np.dot(np.dot(K,np.transpose(x_vect)),P_M)) / w
        estimate_d =np.dot(np.transpose(x_vect),estimate_h)
        error = d_n[i] - estimate_d
        error_vect[i] = error
        estimate_h = estimate_h + np.dot(K,error)
    d = np.ones(X_n.shape) * np.nan
    for i in range(0,n-L):
        x_vect = X_n[i:i+L]
        d[i] = np.dot(np.transpose(estimate_h),x_vect)
    return d,error_vect,estimate_h

if __name__ == '__main__':

    snr = 10
    n = 1000
    fs = 1
    f0 = 0.02
    t = np.arange(n)/fs
    xs = np.cos(2*np.pi*f0*t)
    ws = awgn(xs, snr)

    L =20
    w = 0.1
    delta = 0.2
    xn = ws
    dn = xs
    d,error_vect,estimate_h = RLS_func(w,xs,ws,delta,L)

    plt.figure()
    plt.subplot(211)
    plt.plot(t, ws)
    plt.subplot(212)
    plt.plot(t, d)

    plt.figure()
    plt.plot(error_vect)
    plt.show()