基本子串结构
xtq 的 2023 年集训队论文《一类基础子串数据结构》提及。能够对子串问题减少一定思维量。相比于 sam 只能固定 endpos 向前扩展,基本子串能方便处理子串前后扩展。
这个东西有点科技了,我不是能有自信能解释清楚,这里指自己认为写的比较详细的博客供参考。crashed | 127_127_127
这里不讲详细内容,只做一些和补充,和自己的理解。
相信大家都了解过了基本概念,这里从基本子串的构建讲起。
求 代表元 $ rep $
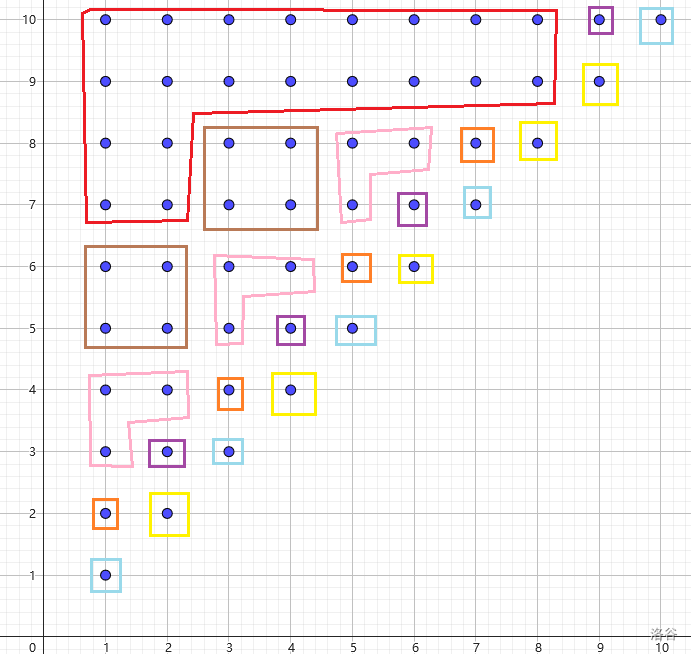
这里的每个行是 SAM 对应的节点,每个列是反 SAM 对应的节点(不理解的非常推荐自己画翻转字符串后的图),想通颜色的对应节点在正反 SAM 中是同一个节点。例如, \((1,6),(2,6)\) 是同 SAM 里一个节点代表的多个子串, \((1,6),(1,5)\) 是同反 SAM 里一个节点代表的多个子串。 \((1,6),(3,8)\) 是完全相同的,在 SAM 是一个节点,所代表的一个相同的子串。在 parent 树上右下角是根节点。一个串的左边是 SAM 的儿子,上面是反 SAM 的儿子。因为 parent 树可能存在多个儿子,所以可能有多个格点对应同一节点。
考虑在格点图上画出 SAM 的 \(link\)。会很自然的发现代表元 \(rep\) 就是 SAM 和反 SAM 对应同时经过的节点。那么倍增求 \(rep\) 的方法已经呼之欲出了。满足 $ r-l+1=len_{正SAM} = len_{反SAM} $ 的子串 \(s_{[l,r]}\) 就是代表元。

如图,行是正 SAM 对应的节点,蓝色圆圈出来的点,就是 SAM 每个节点对应的最长串。同理,黄色五角星圈出来的就是反 SAM 对应的最长串。那么 \(rep\) 就是同时经过的节点,同时被圆和五角星圈出来的点。因为完全相同的块在 SAM 里只出现一次,所以对应的 \(rep\) 是唯一的。
其他点属于的等价类
不难发现,一个点在 DAG 上只有一个出边的话,那么这个点的出现次数一定和指向的节点一致。否则一定不一致(到达的点,代表的子串一定包含自己这个串,如果能到达多个点,说明有不同串,包含这个子串)。
论文指出,由于 SAM 构建的特殊方式,我们可以从后往前合并其他节点。(格点图,同一个等价类一定是个阶梯状的图,所以一定连续,所以直接倒着合并即可)
O(n) 实现
维护一个类似双指针的结构在正反 SAM 上移动,即可 O(n) 求出所有 \(rep\)。
应用
127大神博客给出的例题都推荐做一下
这里再给出两个多校遇到的模板题:
字符串
hdu:7462
实现以下两种操作:
操作1,给定 \(l,r\) ,询问有多少本质不同的串 \(t\) ,满足 \(s[l,r]\) 是 \(t\) 的子串,且 \(occ(s[l,r]) = occ(t)\)
操作2,给定 \(l,r\) ,询问有多少本质不同的串 \(t\) ,满足 \(t\) 是 \(s[l,r]\) 的子串,且 \(occ(s[l,r])= occ(t)\)
询问在线
\(1 \leq |s| \leq 5 \times 10^5\)
构建基本子串结构,询问1,即同一等价类左上角的点数,一定是个矩形,找到询问区间的 \(rep\) 即可。询问2,即同一等价类右下角的点数,对每个等价类,做个前缀和,询问即前缀和减去左下角的点数即可。代码比较容易实现
这里给出样例对应的格点图。(用excel画的,有点丑)

code
#include <bits/stdc++.h>
#define ll long long
#define enl putchar('\n')
#define all(x) (x).begin(),(x).end()
#define debug(x) printf(" "#x":%d\n",x);
using namespace std;
const int MAXN = 5e5 + 5, LOG = 20;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 998244353;
typedef pair<int, int> pii;
char buf[1 << 21], * p1 = buf, * p2 = buf, obuf[1 << 21], * o = obuf, of[35];
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
inline ll qpow(ll a, ll n) { ll res = 1; while (n) { if (n & 1)res = res * a % mod; n >>= 1; a = a * a % mod; }return res; }
template <class T = int>inline T read() { T s = 0, f = 1; char c = gc(); for (; !isdigit(c); c = gc())if (c == '-')f = -1; for (; isdigit(c); c = gc())s = s * 10 + c - '0'; return s * f; }
inline void read(int* a, int n) { for (int i = 1; i <= n; ++i)a[i] = read(); }
inline int inal(char* s) { int n = 0; for (s[0] = gc(); !isalpha(s[0]); s[0] = gc()); for (; isalpha(s[n]); s[++n] = gc()); return s[n] = 0, n; }
inline void outd(int* a, int n) { for (int i = 1; i <= n; ++i)printf("%d ", a[i]); enl; }
int n, m, q;
struct SAM { //最多2n-1个点和3n-4条边
int len[MAXN << 1], link[MAXN << 1], ch[MAXN << 1][26]; //我们记 longest(v) 为其中最长的一个字符串,记 len(v) 为它的长度。
int cnt[MAXN << 1], pos[MAXN], rpos[MAXN << 1], dif[MAXN << 1], id[MAXN << 1];
int cur, lst, siz;
vector<int>e[MAXN << 1];
int fa[MAXN << 1][LOG];
SAM() { clear(); }
void clear() { //设置起始点S
memset(ch, 0, sizeof(int) * (siz + 1) * 26);
memset(cnt, 0, sizeof(int) * (siz + 1));
memset(id, 0, sizeof(int) * (siz + 1));
memset(rpos, 0, sizeof(int) * (siz + 1));
len[0] = 0;
link[0] = -1;
for (int i = 0; i <= siz; ++i)e[i].clear();
siz = 0; //siz设置成0实际上有一个点,方便标记
lst = cur = 0;
}
void extend(int c, int id) {
lst = cur, cur = ++siz;
len[cur] = len[lst] + 1;
cnt[cur] = 1;
for (; ~lst && !ch[lst][c]; lst = link[lst])ch[lst][c] = cur;
if (lst == -1) {
link[cur] = 0;
} else {
int q = ch[lst][c];
if (len[lst] + 1 == len[q]) {
link[cur] = q;
} else { //克隆的点是q(lst的c后继)
int clone = ++siz;
link[clone] = link[q];
len[clone] = len[lst] + 1;
link[cur] = link[q] = clone;
for (; ~lst && ch[lst][c] == q; lst = link[lst])ch[lst][c] = clone;
memcpy(ch[clone], ch[q], sizeof(ch[q]));
}
}
pos[id] = cur;
rpos[cur] = id;
}
void chk(int& x, int v) { if (!x) x = v; else if (v) x = min(x, v); }
void dfs(int x) {
for (int i = 1; i < LOG; ++i)
fa[x][i] = fa[fa[x][i - 1]][i - 1];
for (auto v : e[x]) {
dfs(v);
chk(rpos[x], rpos[v]);
}
}
void build() {
for (int i = 1; i <= siz; ++i) {
e[link[i]].push_back(i);
fa[i][0] = link[i];
dif[i] = len[i] - len[link[i]];
}
dfs(0);
}
void merge() {
for (int i = siz; i >= 1; --i)if (!id[i])
for (int c = 0; c < 26; ++c)if (ch[i][c]) {
id[i] = id[ch[i][c]];
break;
}
}
int FindR(int l, int r) {
int x = pos[r];
for (int i = LOG - 1; i >= 0; --i)
if (len[fa[x][i]] >= r - l + 1)
x = fa[x][i];
return x;
}
}sam, rsam;
char s[MAXN];
vector<int>row[MAXN], col[MAXN], spr[MAXN];
ll sum[MAXN << 1];
void work() {
int Ec = 0;
n = inal(s + 1);
for (int i = 1; i <= n; ++i)
sam.extend(s[i] - 'a', i);
reverse(s + 1, s + n + 1);
for (int i = 1; i <= n; ++i)
rsam.extend(s[i] - 'a', i);
sam.build(); rsam.build();
for (int i = 1; i <= sam.siz; ++i) {
int r = sam.rpos[i],
l = r - sam.len[i] + 1,
u = rsam.FindR(n - r + 1, n - l + 1);
if (r - l + 1 == rsam.len[u]) sam.id[i] = rsam.id[u] = ++Ec;
}
sam.merge(); rsam.merge();
for (int i = sam.siz; i >= 1; --i)
row[sam.id[i]].push_back(i);
for (int i = rsam.siz; i >= 1; --i)
col[rsam.id[i]].push_back(i);
// outd(sam.id, sam.siz);
// outd(rsam.id, rsam.siz);
for (int i = 1; i <= Ec; ++i) {
for (int j = row[i].size() - 1, pre = 0; j >= 0; --j) {
sum[row[i][j]] = sum[pre] + sam.dif[row[i][j]];
pre = row[i][j];
spr[i].push_back(sam.dif[pre]);
}
}
}
ll ans;
void ask() {
int op = read(), l = (read() + ans - 1) % n + 1, r = (read() + ans - 1) % n + 1;
if (l > r)swap(l, r);
int u = sam.FindR(l, r);
int dif = sam.len[u] - (r - l + 1) + 1;
int id = sam.id[u];
if (op == 1) {
ans = 1ll * dif * (sam.len[row[id][0]] - sam.len[u] + 1);
} else {
ans = sum[u];
ll stw = upper_bound(all(spr[id]), dif - 1) - spr[id].begin();
int rowid = row[id].size() - stw;
if (stw) {
ans -= sum[row[id][rowid]];
ans -= 1ll * (dif - 1) * (sam.len[u] - sam.len[row[id][rowid]]);
} else {
ans -= 1ll * (dif - 1) * (sam.len[u] - sam.len[row[id].back()] + 1);
}
}
printf("%lld\n", ans);
}
void solve() {
sam.clear(); rsam.clear();
for (int i = 1; i <= n; ++i)
row[i].clear(), col[i].clear(), spr[i].clear();
memset(sum, 0, sizeof(sum));
ans = 0;
work();
q = read();
while (q--)
ask();
}
signed main(signed argc, char const* argv[]) {
clock_t c1 = clock();
#ifdef LOCAL
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif
//=============================================================
int TxT = 1;
TxT = read();
while (TxT--)
solve();
//=============================================================
#ifdef LOCAL
end :
cerr << "Time Used:" << clock() - c1 << "ms" << endl;
#endif
return 0;
}
串串
hdu:7492
给定一个字符串 \(s\) ,每次可以选择删除两段的一个字符,代价是删除前字符串 \(t\) ,在原串 \(s\) 中出现的次数。求最小代价。
\(1 \leq |s| \leq 10^6\)
注意到,题目相当于格点图从左上角走到右下角的代价,而每步的代价就是这个等价类的 occ ,在每个等价类的周长上实现 dp 即可。因为左上角的 occ 一定小于等于右下的,所以转移考虑正上方,和正左方的点转移即可。用一个拓扑排序或者记忆化都可以维护 dp 的转移顺序。
code
因为是赛时写的代码,所以有点抽象。
#include <bits/stdc++.h>
#define ll long long
#define enl putchar('\n')
#define all(x) (x).begin(),(x).end()
#define debug(x) printf(" "#x":%d\n",x);
using namespace std;
const int MAXN = 1e6 + 5, LOG = 22;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 998244353;
typedef pair<int, int> pii;
char buf[1 << 21], * p1 = buf, * p2 = buf, obuf[1 << 21], * o = obuf, of[35];
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
inline ll qpow(ll a, ll n) { ll res = 1; while (n) { if (n & 1)res = res * a % mod; n >>= 1; a = a * a % mod; }return res; }
template <class T = int>inline T read() { T s = 0, f = 1; char c = gc(); for (; !isdigit(c); c = gc())if (c == '-')f = -1; for (; isdigit(c); c = gc())s = s * 10 + c - '0'; return s * f; }
inline void read(int* a, int n) { for (int i = 1; i <= n; ++i)a[i] = read(); }
inline int inal(char* s) { int n = 0; for (s[0] = gc(); !isalpha(s[0]); s[0] = gc()); for (; isalpha(s[n]); s[++n] = gc()); return s[n] = 0, n; }
inline void outd(int* a, int n) { for (int i = 1; i <= n; ++i)printf("%d ", a[i]); enl; }
int n, m, q;
int du[MAXN];
struct SAM { //最多2n-1个点和3n-4条边
int len[MAXN << 1], link[MAXN << 1], ch[MAXN << 1][26]; //我们记 longest(v) 为其中最长的一个字符串,记 len(v) 为它的长度。
int cnt[MAXN << 1], pos[MAXN], rpos[MAXN << 1], dif[MAXN << 1], id[MAXN << 1];
ll dp[MAXN << 1];
int cur, lst, siz;
vector<int>e[MAXN << 1];
int fa[MAXN << 1][LOG];
SAM() { clear(); }
void clear() { //设置起始点S
memset(ch, 0, sizeof(int) * (siz + 1) * 26);
memset(id, 0, sizeof(int) * (siz + 1));
memset(rpos, 0, sizeof(int) * (siz + 1));
memset(cnt, 0, sizeof(int) * (siz + 1));
for (int i = 0; i <= siz; i++)e[i].clear();
len[0] = 0;
link[0] = -1;
siz = 0; //siz设置成0实际上有一个点,方便标记
lst = cur = 0;
}
void extend(int c, int id) {
lst = cur, cur = ++siz;
len[cur] = len[lst] + 1;
cnt[cur] = 1;
for (; ~lst && !ch[lst][c]; lst = link[lst])ch[lst][c] = cur;
if (lst == -1) {
link[cur] = 0;
} else {
int q = ch[lst][c];
if (len[lst] + 1 == len[q]) {
link[cur] = q;
} else { //克隆的点是q(lst的c后继)
int clone = ++siz;
link[clone] = link[q];
len[clone] = len[lst] + 1;
link[cur] = link[q] = clone;
for (; ~lst && ch[lst][c] == q; lst = link[lst])ch[lst][c] = clone;
memcpy(ch[clone], ch[q], sizeof(ch[q]));
}
}
pos[id] = cur;
rpos[cur] = id;
}
void chk(int& x, int v) { if (!x) x = v; else if (v) x = min(x, v); }
void dfs(int x) {
for (int i = 1; i < LOG; ++i)
fa[x][i] = fa[fa[x][i - 1]][i - 1];
for (auto v : e[x]) {
dfs(v);
cnt[x] += cnt[v];
chk(rpos[x], rpos[v]);
}
}
void build() {
for (int i = 1; i <= siz; ++i) {
e[link[i]].push_back(i);
fa[i][0] = link[i];
dif[i] = len[i] - len[link[i]];
}
dfs(0);
}
void merge() {
for (int i = siz; i >= 1; --i)if (!id[i])
for (int c = 0; c < 26; ++c)if (ch[i][c]) {
id[i] = id[ch[i][c]];
break;
}
}
void dfs_du(int u) { for (auto v : e[u]) dfs_du(v), du[id[u]]++; }
void initdp() {
memset(dp, 0x3f, sizeof(ll) * (siz + 1));
}
int FindR(int l, int r) {
int x = pos[r];
for (signed i = LOG - 1; i >= 0; --i)
if (len[fa[x][i]] >= r - l + 1)
x = fa[x][i];
return x;
}
}sam, rsam;
char s[MAXN];
vector<int>row[MAXN], col[MAXN];
void work() {
int Ec = 0;
sam.clear(), rsam.clear();
n = inal(s + 1);
for (int i = 1; i <= n; ++i)
sam.extend(s[i] - 'a', i);
reverse(s + 1, s + n + 1);
for (int i = 1; i <= n; ++i)
rsam.extend(s[i] - 'a', i);
sam.build(); rsam.build();
for (int i = 1; i <= sam.siz; ++i) {
int r = sam.rpos[i],
l = r - sam.len[i] + 1,
u = rsam.FindR(n - r + 1, n - l + 1);
if (r - l + 1 == rsam.len[u]) sam.id[i] = rsam.id[u] = ++Ec;
}
sam.merge(); rsam.merge();
for (int i = sam.siz; i >= 1; --i)
row[sam.id[i]].push_back(i);
for (int i = rsam.siz; i >= 1; --i)
col[rsam.id[i]].push_back(i);
sam.dfs_du(0); rsam.dfs_du(0);
auto topsort = [&]() -> void {
queue<int>q;
sam.initdp(), rsam.initdp();
for (int i = 1; i <= Ec; ++i)
if (!du[i]) {
for (auto pos : row[i])sam.dp[pos] = n - sam.len[pos];
for (auto pos : col[i])rsam.dp[pos] = n - rsam.len[pos];
q.push(i);
}
ll ans = INF;
while (!q.empty()) {
int i = q.front(); q.pop();
int R = row[i].size(), C = col[i].size();
int j = R - 1;
ll rowval = sam.dp[row[i][j]], occ = sam.cnt[row[i][0]], colval;
for (int x = 0; x < C; ++x) {
colval = rsam.dp[col[i][x]];
while (sam.dif[row[i][j]] <= x) {
ll val = min(sam.dp[row[i][j]] + sam.dif[row[i][j]] * occ, colval + (j + 1) * occ);
int nxt = sam.link[row[i][j]];
if (!nxt) {
ans = min(ans, val);
} else {
sam.dp[nxt] = min(sam.dp[nxt], val);
du[sam.id[nxt]]--;
if (!du[sam.id[nxt]])
q.push(sam.id[nxt]);
}
--j;
rowval = sam.dp[row[i][j]];
}
ll val = min(rsam.dp[col[i][x]] + rsam.dif[col[i][x]] * occ, rowval + (x + 1) * occ);
int nxt = rsam.link[col[i][x]];
if (!nxt) {
ans = min(ans, val);
} else {
rsam.dp[nxt] = min(rsam.dp[nxt], val);
du[rsam.id[nxt]]--;
if (!du[rsam.id[nxt]])
q.push(rsam.id[nxt]);
}
}
while (j >= 0) {
ll val = min(sam.dp[row[i][j]] + sam.dif[row[i][j]] * occ, colval + (j + 1) * occ);
if (!sam.link[row[i][j]]) {
ans = min(ans, val);
} else {
int nxt = sam.link[row[i][j]];
sam.dp[nxt] = min(sam.dp[nxt], val);
du[sam.id[nxt]]--;
if (!du[sam.id[nxt]])
q.push(sam.id[nxt]);
}
--j;
}
}
printf("%lld\n", ans);
};
topsort();
for (int i = 1; i <= Ec; ++i)
col[i].clear(), row[i].clear();
memset(du + 1, 0, sizeof(int) * Ec);
}
void solve() {
work();
}
signed main(signed argc, char const* argv[]) {
clock_t c1 = clock();
#ifdef LOCAL
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif
//=============================================================
int TxT = 1;
TxT = read();
while (TxT--)
solve();
//=============================================================
#ifdef LOCAL
end :
cerr << "Time Used:" << clock() - c1 << "ms" << endl;
#endif
return 0;
}
parent 树的树链剖分
我们直接说结论。
树剖的每一条重链都会延伸到叶子,而所有叶子的 \(occ = 1\) 。也就是说,每一条链的链底的长度标号都是连续的。(在格点图中,最左上角的那一块,所有 \(occ = 1\) 的 SAM 节点都对应一条链)
我们重新对所有子串映射成新的点,\((这个点在反串的重链标号,长度)\)。不难看出,这个新编号,是双射的。这样我们就很好的用 $ O(n) $ 的空间刻画出,所有的子串,并且对应了正反 SAM 上的点。
-
对于反串 SAM 的一个结点和一条链,其代表的所有等价类在 \(xOy\) 平面上为一条竖线段。
-
对于正串 SAM 的一个结点,其代表的所有等价类在 \(xOy\) 平面上为一条斜线段。(但链不是)
反串的重链是同一条,长度不断增加,所以是竖线段。
正串的一个节点,长度不断增加的的同时,对应的反串所在的链增加(因为链是连续的),所以是斜线。(详细看127大神的图)
现在我们能看 [BJWC2018] Border 的四种求法
在 SAM 里找到右边界,反 SAM 找到左边界。然后逐渐增加简短长度,看看是否匹配即可。匹配即,反串 SAM 的竖线和正串 SAM 的斜线有交点。询问离线挂在正串 SAM 重链上。反串 SAM 的竖线构成 \(log\) 个竖线段。找交点就是把正串 SAM 的点逐个加入线段树,线段树上找靠右的最大即可。详细写法参开127的题解
p.s. 推荐学学 \(border\) 理论的解法。
和b4写法一致,只需要改几行代码就行。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号