【CF1481D】AB Graph 题解

原题链接

题意简介

给你一个有向图。图中任意两点间都可以直接往来(含有 n*(n-1) 条边，无重边和自环)。每条边上有一个字母 a 或 b。现要求你找出一条长度为 m 的路径(可重复经过)，使路径上的字母构成的字符串为回文串。

思路分析

跟 C 题类似的分类讨论寻找方案。

首先，如果存在同一字母路径构成的环，那么只需要让路径全程都在这个环上就行了。

如果不满足上一条，表明任意两点间的两条有向边的字母不同。那么就有了下面的情形。

1. m 是 4 的倍数。那么只需要找到一个出边中有两种字母的点(如下图点2)，制造出 abba 或 baab 的循环就行了。

   显然，n>2 时必然存在这样的点，不然必会形成同字母环，与“不满足第一条”相矛盾。

2. m 是奇数。那么随便找两个点走就行了，必然形成 ababa 或是 babab。

3. m 是 2 的倍数但不是 4 的倍数。找到一个出边有两种字母的点(还是那个点2)，然后从与之相连的另一个边开始(如点1)，先进行前面的循环，然后（进行中间循环）进入点2，再沿与进入点2的边字母相同的出边到达另一个点(点3)，然后在这两个点间进行后面的循环。

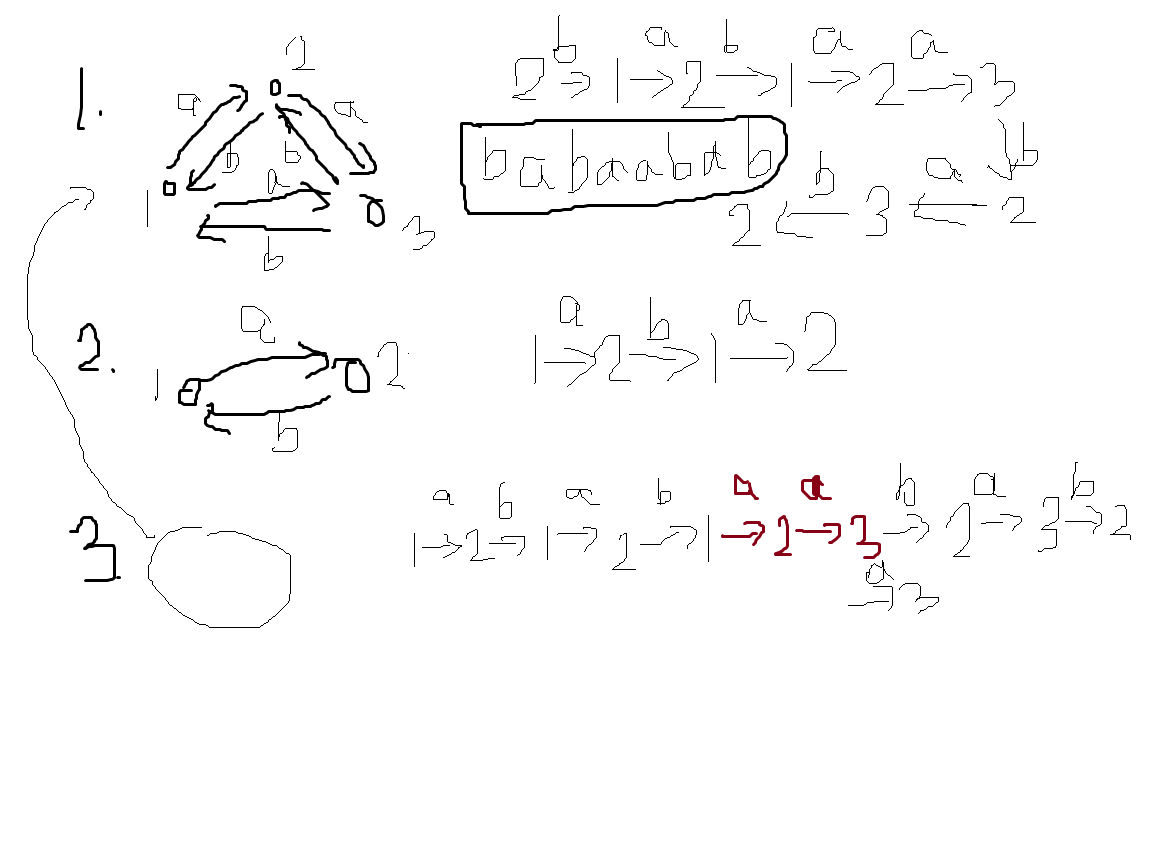
由上面的分析我们不难看出，唯一输出 No 的情形是 n=2 、没有同字母环且 m 是偶数的情形。

至于找环，我使用的是dfs序+栈的写法。

代码库

写得很丑，见谅。

#include <cstdio>
#include <cstring>
#define rep(i,a,b) for(int i=a;i<=b;i++)
inline int min(const int&a,const int&b){
    return a<b?a:b;
}
const int N=1005;
int t,n,m,dfn[N],st[N],top,cyc[N],cn; bool vis[N],isi=0;
char s[N][N];
void clear(){
    rep(i,1,n) vis[i]=0,dfn[i]=0;
    top=0; isi=0; cn=0;
}
void dfs(int u,const char j){
    //printf("(%d %c)\n",u,j);
    static int c=0;
    if(isi) return;
    dfn[u]=++c; st[++top]=u; vis[u]=1;
    rep(v,1,n){
        if(s[u][v]==j){
            if(!dfn[v]) dfs(v,j);
            else if(vis[v]){
                isi=1;
                while(st[top]!=v){
                    cyc[++cn]=st[top];
                    vis[st[top--]]=0;
                }
                cyc[++cn]=v;
                break;
            }
        }
    }
    top--; vis[u]=0;
}
int main(){
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&m);
        rep(i,1,n) scanf(" %s",s[i]+1);
        clear();
        rep(i,1,n){
            if(!dfn[i]) dfs(i,'a');
            if(isi) break;
        }
        if(isi){
            puts("YES");
            rep(i,1,m+1) printf("%d ",cyc[cn-(i-1)%cn]);
            puts(""); continue;
        }
        clear();
        rep(i,1,n){
            if(!dfn[i]) dfs(i,'b');
            if(isi) break;
        }
        if(isi){
            puts("YES");
            rep(i,1,m+1) printf("%d ",cyc[cn-(i-1)%cn]);
            puts(""); continue;
        }
        // 到这里表明没有找到环
        if(m&1){
            puts("YES");
            rep(i,1,m+1) printf("%d ",(i&1)+1); // 点1和点2之间转就行了
            puts(""); continue;
        }
        if(n==2){
            puts("NO"); continue;
        }
        int sp=0; // 找出特殊点
        rep(i,1,n){
            bool s1=0,s2=0;
            rep(j,1,n){
                if(s[i][j]=='a') s1=1;
                else if(s[i][j]=='b') s2=1;
            }
            if(s1&&s2){ sp=i; break; }
        }
        //printf("%d ",sp);
        puts("YES");
        if(m%4==0){
            rep(i,1,n){
                if(s[sp][i]=='a'){
                    rep(j,1,m/4) printf("%d %d ",sp,i);
                    break;
                }
            }
            printf("%d ",sp);
            rep(i,1,n){
                if(s[sp][i]=='b'){
                    rep(j,1,m/4) printf("%d %d ",i,sp);
                    break;
                }
            }
            puts("");
        }else{
            int p=0;
            rep(i,1,n){
                if(s[i][sp]=='a'){
                    p=i;
                    rep(j,1,(m-2)/4) printf("%d %d ",i,sp);
                    break;
                }
            }
            printf("%d ",p);
            rep(i,1,n){
                if(s[i][sp]=='b'){
                    rep(j,1,(m+2)/4) printf("%d %d ",sp,i);
                    break;
                }
            }
            puts("");
        }
    }
    return 0;
}