【滚动数组】【状压DP】NOI2001炮兵阵地

题目描述 司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成,地图的每一格可能是山地(用“H” 表示),也可能是平原(用“P”表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示: 如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。 输入输出格式 输入格式: 第一行包含两个由空格分割开的正整数,分别表示N和M; 接下来的N行,每一行含有连续的M个字符(‘P’或者‘H’),中间没有空格。按顺序表示地图中每一行的数据。N≤100;M≤10。 输出格式: 仅一行,包含一个整数K,表示最多能摆放的炮兵部队的数量。 输入输出样例 输入样例#1: 复制 5 4 PHPP PPHH PPPP PHPP PHHP 输出样例#1: 复制 6
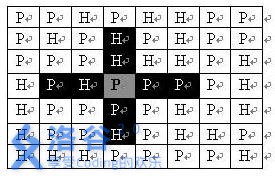
这道题依旧状压,区别就是这道题和前两行的状态都有关系
那么很容易想到dp[i][pr][l1]代表第i行,当前状态编号为pr,上一行为l1,
但是算一下会发现空间并不够,
这是就有一个高级的东西,叫滚动数组,因为当前行的状态只与前两行有关
所以我们用的时候把状态第一维%3,再算一下空间复杂度,就够了
这道题我卡了一上午
(situ[pr]&can[2])==0和situ[pr]&can[2]==0是不一样的
包括!(situ[pr]&can[2])和!situ[pr]&can[2]也是不一样的
得出教训
状压DP能多加括号就多加
还有一点,如果读入时候是字符串
处理时候要倒过来,因为字符的第一位其实是我们要的最高位
然后代码在此
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #define N 151 5 #define M 15 6 using namespace std;typedef long long ll; 7 int n,m,pp,ans=-1; 8 int can[N],dp[3][1<<11][1<<11],situ[1<<11],num[1<<11]; 9 char tt[M]; 10 void search(int id,int sit,int nn) 11 { 12 if(id>m){situ[++pp]=sit;num[pp]=nn;return;} 13 search(id+3,sit+(1<<id-1),nn+1); 14 search(id+1,sit,nn); 15 } 16 int main() 17 { 18 memset(dp,~0x3f,sizeof(dp)); 19 scanf("%d%d",&n,&m); 20 for(int i=1;i<=n;i++) 21 { 22 scanf("%s",tt+1); 23 for(int j=1;j<=m;j++) 24 if(tt[j]=='H') 25 can[i]|=1<<(m-j); 26 } 27 search(1,0,0); 28 for(int i=1;i<=pp;i++) 29 if((situ[i]&can[1])==0) 30 dp[1][i][0]=num[i]; 31 for(int l1=1;l1<=pp;l1++)//line 1 32 for(int pr=1;pr<=pp;pr++)//line 2 33 if((situ[pr]&can[2])==0 && (situ[pr]&situ[l1])==0 && (situ[l1]&can[1])==0) 34 dp[2][pr][l1]=max(num[pr]+dp[1][l1][0],dp[2][pr][l1]); 35 for(int i=3;i<=n;i++) 36 for(int pr=1;pr<=pp;pr++) 37 if((can[i]&situ[pr])==0) 38 for(int l1=1;l1<=pp;l1++) 39 if((situ[l1]&situ[pr])==0 && (situ[l1]&can[i-1])==0) 40 for(int l2=1;l2<=pp;l2++) 41 if((situ[l2]&situ[l1])==0 && (situ[l2]&situ[pr])==0 && (situ[l2]&can[i-2])==0) 42 dp[i%3][pr][l1]=max(dp[(i-1)%3][l1][l2]+num[pr],dp[i%3][pr][l1]); 43 for(int l1=1;l1<=pp;l1++)//line n-1 44 for(int pr=1;pr<=pp;pr++)//line n 45 ans=max(ans,dp[n%3][pr][l1]); 46 printf("%d\n",ans); 47 return 0; 48 }


