NOI2015程序自动分析【并查集+离散化】【做题报告】
这是一道国赛水题
题意:(来自洛谷)
题目描述
在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。
考虑一个约束满足问题的简化版本:假设x1,x2,x3...代表程序中出现的变量,给定n个形如xi=xj或xi≠xj的变量相等/不等的约束条件,请判定是否可以分别为每一个变量赋予恰当的值,使得上述所有约束条件同时被满足。例如,一个问题中的约束条件为:x1=x2,x2=x3,x3=x4,x4≠x1,这些约束条件显然是不可能同时被满足的,因此这个问题应判定为不可被满足。
现在给出一些约束满足问题,请分别对它们进行判定。
输入输出格式
输入格式:
从文件prog.in中读入数据。
输入文件的第1行包含1个正整数t,表示需要判定的问题个数。注意这些问题之间是相互独立的。
对于每个问题,包含若干行:
第1行包含1个正整数n,表示该问题中需要被满足的约束条件个数。接下来n行,每行包括3个整数i,j,e,描述1个相等/不等的约束条件,相邻整数之间用单个空格隔开。若e=1,则该约束条件为xi=xj;若�e=0,则该约束条件为xi≠xj;
输出格式:
输出到文件 prog.out 中。
输出文件包括t行。
输出文件的第 k行输出一个字符串“ YES” 或者“ NO”(不包含引号,字母全部大写),“ YES” 表示输入中的第k个问题判定为可以被满足,“ NO” 表示不可被满足。
输入输出样例
说明
【样例解释1】
在第一个问题中,约束条件为:x1=x2,x1≠x2。这两个约束条件互相矛盾,因此不可被同时满足。
在第二个问题中,约束条件为:x1=x2,x1=x2。这两个约束条件是等价的,可以被同时满足。
【样例说明2】
在第一个问题中,约束条件有三个:x1=x2,x2=x3,x3=x1。只需赋值使得x1=x1=x1,即可同时满足所有的约束条件。
在第二个问题中,约束条件有四个:x1=x2,x2=x3,x3=x4,x4≠x1。由前三个约束条件可以推出x1=x2=x3=x4,然而最后一个约束条件却要求x1≠x4,因此不可被满足。
【数据范围】
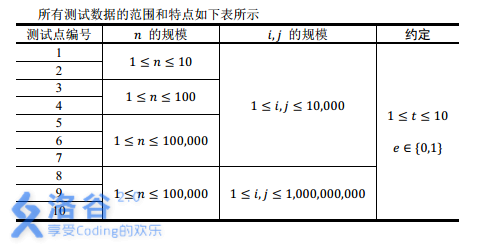
【时限2s,内存512M】
这道题思路还是很水的,还是带权并查集,val值1和0进行合并;然后路径压缩更新;,十分钟出代码
然后。。。
看数据范围可以知道需要离散化,这个在我上一个博客已经说了,就不再赘述
然后清一下数组,数组开大些,然后。。。
这是为什么呢
看这组数
8 11 0
8 13 0
11 13 0
按我的方式就会WA
所以我后桌大佬的思路就来了
先把所有的相等的进行合并
然后再判定不相等
最后。。

考前摸jx,暴力能AC;
考前摸jx,高一拿省一!
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 using namespace std; 5 int T,n,x,y; 6 bool ans=0; 7 int f[101111*2],opt[101111*2],val[101111*2]; 8 struct node{ 9 int val,hs,no; 10 }nd[101111*2]; 11 bool cmp1(node a,node b) 12 {return a.val<b.val;} 13 bool cmp2(node a,node b) 14 {return a.no<b.no;} 15 int find(int x) 16 { 17 if(f[x]==x)return x; 18 int ff=find(f[x]); 19 val[x]=(val[x]+val[f[x]])%2; 20 return f[x]=ff; 21 } 22 int main() 23 { 24 //freopen("testdata.in","r",stdin); 25 scanf("%d",&T); 26 while(T--) 27 { 28 memset(val,0,sizeof(val)); 29 ans=0; 30 scanf("%d",&n); 31 for(int i=1;i<=n;i++) 32 { 33 scanf("%d%d%d",&x,&y,&opt[i]); 34 nd[i].val=x; 35 nd[i+n].val=y; 36 nd[i].no=nd[i+n].no=i; 37 } 38 sort(nd+1,nd+2*n+1,cmp1); 39 int tt=0; 40 for(int i=1;i<=2*n;i++) 41 { 42 if(nd[i].val==nd[i-1].val)nd[i].hs=tt; 43 else nd[i].hs=++tt; 44 f[tt]=tt; 45 } 46 sort(nd+1,nd+2*n+1,cmp2); 47 int cnt=0; 48 for(int i=1;i<=2*n;i+=2) 49 { 50 cnt=i/2+1; 51 if(opt[cnt]==0)continue; 52 x=nd[i].hs,y=nd[i+1].hs; 53 int fx=find(x),fy=find(y); 54 if(fx==fy) 55 { 56 continue; 57 }else 58 { 59 val[fx]=(val[x]+val[y])%2; 60 f[fx]=fy; 61 } 62 } 63 for(int i=1;i<=2*n;i+=2) 64 { 65 cnt=i/2+1; 66 if(opt[cnt]==1)continue; 67 x=nd[i].hs,y=nd[i+1].hs; 68 int fx=find(x),fy=find(y); 69 if(fx==fy) 70 { 71 if(val[x]==val[y]) 72 { 73 ans=1; 74 break; 75 } 76 } 77 } 78 if(ans==1)printf("NO\n"); 79 else printf("YES\n"); 80 } 81 return 0; 82 }

