VIJOS P1144 /LNSYOJ148小胖守皇宫【做题报告】
这是一道树形DP;
题意
题目描述
huyichen世子事件后,xuzhenyi成了皇上特聘的御前一品侍卫。 皇宫以午门为起点,直到后宫嫔妃们的寝宫,呈一棵树的形状;某些宫殿间可以互相望见。大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。 可是xuzhenyi手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。 帮助xuzhenyi布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
输入格式
输入文件中数据表示一棵树,描述如下:
第1行 nn,表示树中结点的数目。
第2行至第n+1n+1行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号i(0<i≤n)i(0<i≤n),在该宫殿安置侍卫所需的经费kk,该边的儿子数mm,接下来mm个数,分别是这个节点的mm个儿子的标号r1,r2,...,rmr1,r2,...,rm。
对于一个n(0<n≤1500)n(0<n≤1500)个结点的树,结点标号在1到nn之间,且标号不重复。
输出格式
输出文件仅包含一个数,为所求的最少的经费。
样例一
input
6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0
output
25

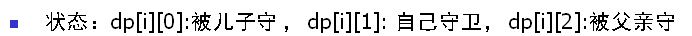
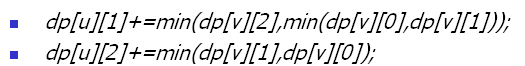
这两种状态比较简单比较好想

dp[u][0]就特别神奇
dp[u][0]需要加上这个min为了防止儿子选的全都是dp[u][0],这是非常巧妙的一个想法
注意叶节点更新,dp[u][0]为inf,dp[u][1]=val[u],dp[u][2]=0;
还有输出时候根节点是没有父亲的!!,两个进行比较就行,要不会WAWAWA
然后就A了

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #define N 1511 5 using namespace std; 6 int n,id,son,so,cnt=1,root,ww; 7 int head[N],val[N],indegree[N],dp[N][3];//0:son,1,mine,2,fa 8 struct star{int to,nxt;}edge[N*2]; 9 inline void add(int u,int v) 10 { 11 edge[cnt].nxt=head[u]; 12 edge[cnt].to=v; 13 head[u]=cnt++; 14 indegree[v]++; 15 } 16 void DP(int now,int fa) 17 { 18 int mi=0x7f7f7f7f-10; 19 for(int i=head[now];i!=-1;i=edge[i].nxt) 20 { 21 int to=edge[i].to; 22 if(to==fa)continue; 23 DP(to,now); 24 dp[now][1]+=min(min(dp[to][0],dp[to][1]),dp[to][2]); 25 dp[now][2]+=min(dp[to][1],dp[to][0]); 26 dp[now][0]+=min(dp[to][0],dp[to][1]); 27 mi=min(mi,dp[to][1]-min(dp[to][1],dp[to][0])); 28 } 29 dp[now][0]+=mi; 30 dp[now][1]+=val[now]; 31 } 32 int main() 33 { 34 //freopen("misaki.in","r",stdin); 35 memset(head,-1,sizeof(head)); 36 scanf("%d",&n); 37 for(int i=1;i<=n;i++) 38 { 39 scanf("%d%d%d",&id,&ww,&son);val[id]=ww; 40 for(int j=1;j<=son;j++) 41 { 42 scanf("%d",&so); 43 add(id,so); 44 add(so,id); 45 } 46 }//build 47 DP(1,-1); 48 printf("%d",min(dp[1][0],dp[1][1])); 49 return 0; 50 }


