实验1:决策树算法实验

实验一:决策树算法实验
| 20大数据三班 | 20大数据三班 |
| ---- | ---- | ---- |
|作业要求|作业链接|
| 学号 | 201613336 |
实验目的
- 理解决策树算法原理,掌握决策树算法框架
- 理解决策树学习算法的特征选择,树的生成和树的剪枝;
- 能根据不同的数据类型,选择不同的决策树算法;
- 针对特定应用场景及数据,能应用决策树算法解决实际问题。
实验内容
- 设计算法实现熵、经验条件熵、信息增益等方法。
- 实现ID3算法。
- 熟悉sklearn库中的决策树算法
- 针对iris数据集、应用skelearn决策树进行类别预测
- 针对iris数据集,利用自编决策树算法进行类别预测。
实验报告要求
- 对照实验内容,撰写实验过程,算法,及测试结果;
- 代码规范化、命名规则、注释;
- 分析核心算法的复杂度;
- 查阅文献、讨论ID3、C4.5算法的应用场景
- 查阅文献、分析决策树剪枝策略。
实验内容及结果
实验代码及截图
- 导入模块所使用的包
点击查看代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from _collections import _count_elements
import math
from math import log
import pprint
点击查看代码
def createDataSet():
dataSet = [[0, 0, 0, 0, 'no'], # 数据集
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况',u'类别'] # 分类属性
return dataSet, labels # 返回数据集和分类属性
点击查看代码
dataSet, features = createDataSet()
trainData = pd.DataFrame(dataSet,columns=features)
print(trainData)
4.采用ID3算法计算信息增益
点击查看代码
def calcShannonEnt(dataSet):
numEntires = len(dataSet) # 返回数据集的行数
labelCounts = {} # 保存每个标签(Label)出现次数的字典
for featVec in dataSet: # 对每组特征向量进行统计
currentLabel = featVec[-1] # 提取标签(Label)信息
if currentLabel not in labelCounts.keys(): # 如果标签(Label)没有放入统计次数的字典,添加进去
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1 # Label计数
shannonEnt = 0.0 # 经验熵(香农熵)
for key in labelCounts: # 计算香农熵
prob = float(labelCounts[key]) / numEntires # 选择该标签(Label)的概率
shannonEnt -= prob * log(prob, 2) # 利用公式计算
return shannonEnt # 返回经验熵(香农熵)
"""
函数说明:按照给定特征划分数据集
Parameters:
dataSet - 待划分的数据集
axis - 划分数据集的特征
value - 需要返回的特征的值
"""
def splitDataSet(dataSet, axis, value):
retDataSet = [] # 创建返回的数据集列表
for featVec in dataSet: # 遍历数据集
if featVec[axis] == value:
reducedFeatVec = featVec[:axis] # 去掉axis特征
reducedFeatVec.extend(featVec[axis + 1:]) # 将符合条件的添加到返回的数据集
retDataSet.append(reducedFeatVec)
return retDataSet # 返回划分后的数据集
"""
函数说明:选择最优特征
Parameters:
dataSet - 数据集
Returns:
bestFeature - 信息增益最大的(最优)特征的索引值
"""
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 # 特征数量
baseEntropy = calcShannonEnt(dataSet) # 计算数据集的香农熵
bestInfoGain = 0.0 # 信息增益
bestFeature = -1 # 最优特征的索引值
for i in range(numFeatures): # 遍历所有特征
# 获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
uniqueVals = set(featList) # 创建set集合{},元素不可重复
newEntropy = 0.0 # 经验条件熵
for value in uniqueVals: # 计算信息增益
subDataSet = splitDataSet(dataSet, i, value) # subDataSet划分后的子集
prob = len(subDataSet) / float(len(dataSet)) # 计算子集的概率
newEntropy += prob * calcShannonEnt(subDataSet) # 根据公式计算经验条件熵
infoGain = baseEntropy - newEntropy # 信息增益
# for j in range(numFeatures):
# print(j)
print("第%d个特征的增益为%.3f" % (i, infoGain)) # 打印每个特征的信息增益
# print(infoGain.dtype)
if (infoGain > bestInfoGain): # 计算信息增益
bestInfoGain = infoGain # 更新信息增益,找到最大的信息增益
bestFeature = i # 记录信息增益最大的特征的索引值
return bestFeature # 返回信息增益最大的特征的索引值
点击查看代码
from math import log
import operator
"""
函数说明:创建测试数据集
"""
def createDataSet():
dataSet = [[0, 0, 0, 0, 'no'], # 数据集
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels = ['年龄', '有工作', '有自己的房子', '信贷情况'] # 分类属性
return dataSet, labels # 返回数据集和分类属性
"""
函数说明:计算给定数据集的经验熵(香农熵)
Parameters:
dataSet - 数据集
Returns:
shannonEnt - 经验熵(香农熵)
"""
def calcShannonEnt(dataSet):
numEntires = len(dataSet) # 返回数据集的行数
labelCounts = {} # 保存每个标签(Label)出现次数的字典
for featVec in dataSet: # 对每组特征向量进行统计
currentLabel = featVec[-1] # 提取标签(Label)信息
if currentLabel not in labelCounts.keys(): # 如果标签(Label)没有放入统计次数的字典,添加进去
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1 # Label计数
shannonEnt = 0.0 # 经验熵(香农熵)
for key in labelCounts: # 计算香农熵
prob = float(labelCounts[key]) / numEntires # 选择该标签(Label)的概率
shannonEnt -= prob * log(prob, 2) # 利用公式计算
return shannonEnt # 返回经验熵(香农熵)
"""
函数说明:按照给定特征划分数据集
Parameters:
dataSet - 待划分的数据集
axis - 划分数据集的特征
value - 需要返回的特征的值
"""
def splitDataSet(dataSet, axis, value):
retDataSet = [] # 创建返回的数据集列表
for featVec in dataSet: # 遍历数据集
if featVec[axis] == value:
reducedFeatVec = featVec[:axis] # 去掉axis特征
reducedFeatVec.extend(featVec[axis + 1:]) # 将符合条件的添加到返回的数据集
retDataSet.append(reducedFeatVec)
return retDataSet # 返回划分后的数据集
"""
函数说明:选择最优特征
Parameters:
dataSet - 数据集
Returns:
bestFeature - 信息增益最大的(最优)特征的索引值
"""
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 # 特征数量
baseEntropy = calcShannonEnt(dataSet) # 计算数据集的香农熵
bestInfoGain = 0.0 # 信息增益
bestFeature = -1 # 最优特征的索引值
for i in range(numFeatures): # 遍历所有特征
# 获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
uniqueVals = set(featList) # 创建set集合{},元素不可重复
newEntropy = 0.0 # 经验条件熵
for value in uniqueVals: # 计算信息增益
subDataSet = splitDataSet(dataSet, i, value) # subDataSet划分后的子集
prob = len(subDataSet) / float(len(dataSet)) # 计算子集的概率
newEntropy += prob * calcShannonEnt(subDataSet) # 根据公式计算经验条件熵
infoGain = baseEntropy - newEntropy # 信息增益
print("第%d个特征的增益为%.3f" % (i, infoGain)) # 打印每个特征的信息增益
if (infoGain > bestInfoGain): # 计算信息增益
bestInfoGain = infoGain # 更新信息增益,找到最大的信息增益
bestFeature = i # 记录信息增益最大的特征的索引值
return bestFeature # 返回信息增益最大的特征的索引值
"""
函数说明:统计classList中出现此处最多的元素(类标签)
Parameters:
classList - 类标签列表
Returns:
sortedClassCount[0][0] - 出现此处最多的元素(类标签)
"""
def majorityCnt(classList):
classCount = {}
for vote in classList: # 统计classList中每个元素出现的次数
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) # 根据字典的值降序排序
return sortedClassCount[0][0] # 返回classList中出现次数最多的元素
"""
函数说明:递归构建决策树
Parameters:
dataSet - 训练数据集
labels - 分类属性标签
featLabels - 存储选择的最优特征标签
Returns:
myTree - 决策树
"""
def createTree(dataSet, labels, featLabels):
classList = [example[-1] for example in dataSet] # 取分类标签(是否放贷:yes or no)
if classList.count(classList[0]) == len(classList): # 如果类别完全相同则停止继续划分
return classList[0]
if len(dataSet[0]) == 1: # 遍历完所有特征时返回出现次数最多的类标签
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet) # 选择最优特征
bestFeatLabel = labels[bestFeat] # 最优特征的标签
featLabels.append(bestFeatLabel)
myTree = {bestFeatLabel: {}} # 根据最优特征的标签生成树
del (labels[bestFeat]) # 删除已经使用特征标签
featValues = [example[bestFeat] for example in dataSet] # 得到训练集中所有最优特征的属性值
uniqueVals = set(featValues) # 去掉重复的属性值
for value in uniqueVals:
subLabels = labels[:]
# 递归调用函数createTree(),遍历特征,创建决策树。
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, featLabels)
return myTree
"""
函数说明:使用决策树执行分类
Parameters:
inputTree - 已经生成的决策树
featLabels - 存储选择的最优特征标签
testVec - 测试数据列表,顺序对应最优特征标签
Returns:
classLabel - 分类结果
"""
def classify(inputTree, featLabels, testVec):
firstStr = next(iter(inputTree)) # 获取决策树结点
secondDict = inputTree[firstStr] # 下一个字典
featIndex = featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex] == key:
if type(secondDict[key]).__name__ == 'dict':
classLabel = classify(secondDict[key], featLabels, testVec)
else:
classLabel = secondDict[key]
return classLabel
'''
函数说明:获取决策树叶子结点的数目
Parameters:
myTree - 决策树
Returns:
numLeafs - 决策树的叶子结点的数目
'''
def getNumLeafs(myTree):
numLeafs = 0 # 初始化叶子
# python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性,
# 可以使用list(myTree.keys())[0]
firstStr = next(iter(myTree))
secondDict = myTree[firstStr] # 获取下一组字典
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict': # 测试该结点是否为字典,如果不是字典,代表此结点为叶子结点
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
"""
函数说明:获取决策树的层数
Parameters:
myTree - 决策树
Returns:
maxDepth - 决策树的层数
"""
def getTreeDepth(myTree):
maxDepth = 0 # 初始化决策树深度
# python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性,
# 可以使用list(myTree.keys())[0]
firstStr = next(iter(myTree))
secondDict = myTree[firstStr] # 获取下一个字典
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict': # 测试该结点是否为字典,如果不是字典,代表此结点为叶子结点
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
if thisDepth > maxDepth:
maxDepth = thisDepth # 更新层数
return maxDepth
'''
函数说明:绘制结点
Parameters:
nodeTxt - 结点名
centerPt - 文本位置
parentPt - 标注的箭头位置
nodeType - 结点格式
'''
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
arrow_args = dict(arrowstyle="<-") # 定义箭头格式
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14) # 设置中文字体
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', # 绘制结点
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args, fontproperties=font)
'''
函数说明:标注有向边属性值
Parameters:
cntrPt、parentPt - 用于计算标注位置
txtString - 标注的内容
'''
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0] # 计算标注位置
yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
"""
函数说明:绘制决策树
Parameters:
myTree - 决策树(字典)
parentPt - 标注的内容
nodeTxt - 结点名
"""
def plotTree(myTree, parentPt, nodeTxt):
decisionNode = dict(boxstyle="sawtooth", fc="0.8") # 设置结点格式
leafNode = dict(boxstyle="round4", fc="0.8") # 设置叶结点格式
numLeafs = getNumLeafs(myTree) # 获取决策树叶结点数目,决定了树的宽度
depth = getTreeDepth(myTree) # 获取决策树层数
firstStr = next(iter(myTree)) # 下个字典
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff) # 中心位置
plotMidText(cntrPt, parentPt, nodeTxt) # 标注有向边属性值
plotNode(firstStr, cntrPt, parentPt, decisionNode) # 绘制结点
secondDict = myTree[firstStr] # 下一个字典,也就是继续绘制子结点
plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD # y偏移
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict': # 测试该结点是否为字典,如果不是字典,代表此结点为叶子结点
plotTree(secondDict[key], cntrPt, str(key)) # 不是叶结点,递归调用继续绘制
else: # 如果是叶结点,绘制叶结点,并标注有向边属性值
plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD
"""
函数说明:创建绘制面板
Parameters:
inTree - 决策树(字典)
"""
def createPlot(inTree):
fig = plt.figure(1, facecolor='white') # 创建fig
fig.clf() # 清空fig
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # 去掉x、y轴
plotTree.totalW = float(getNumLeafs(inTree)) # 获取决策树叶结点数目
plotTree.totalD = float(getTreeDepth(inTree)) # 获取决策树层数
plotTree.xOff = -0.5 / plotTree.totalW;
plotTree.yOff = 1.0; # x偏移
plotTree(inTree, (0.5, 1.0), '') # 绘制决策树
plt.savefig("./BT.png")
plt.show()
if __name__ == '__main__':
dataSet, labels = createDataSet()
featLabels = []
myTree = createTree(dataSet, labels, featLabels)
print("决策树结构:{}".format(myTree))
testVec = [0, 1, 1, 1] # 测试数据
result = classify(myTree, featLabels, testVec)
if result == 'yes':
print('可贷')
if result == 'no':
print('不可贷')
createPlot(mytree)
- 预测结果

- 决策树结构可视化
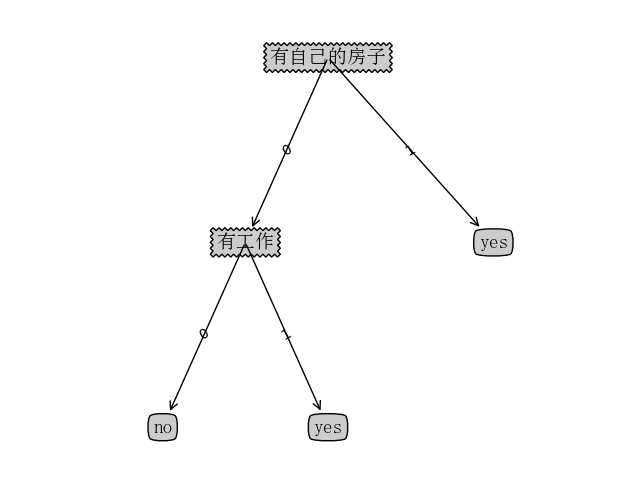
- 使用sklearn中决策树算法
点击查看代码
#author:qiao_px
#@Time 2022/10/19 17:06
#@File DT.py
import numpy as np
import random
from sklearn import tree
from graphviz import Source
import pandas as pd
import re
def origalData():
dataSet = [[0, 0, 0, 0, 'no'], # 数据集
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别'] # 分类属性
return dataSet, labels # 返回数据集和分类属性
if __name__ == '__main__':
dataset,labels = origalData()
datasetFrame = pd.DataFrame(dataset)
print("datasetFrame:{}".format(datasetFrame))
X_train = datasetFrame.iloc[:,:-1]
Y_train = datasetFrame.iloc[:,4:]
a = np.column_stack((Y_train,X_train))
clf = tree.DecisionTreeClassifier(criterion='gini',max_depth=4)
clf =clf.fit(X_train,Y_train)
graph = Source(tree.export_graphviz(clf,out_file=None))
graph.format='png'
graph.render('dtYesNo',view=True)
print('X_train:{}\nY_train:{}'.format(X_train,Y_train))
# print("dataset:{}\nlabels:{}".format(dataset,labels))
- 应用skearn中决策树算法gini结果
- 针对iris数据集,应用sklearn的决策树算法进行类别预测
点击查看代码
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data,columns=iris.feature_names)
df['label']=iris.target
df.columns = ['speal length','speal width','petal length','petal width','label']
data = np.array(df.iloc[:100,[0,1,-1]])
print('data:')
print(data)
if __name__ == '__main__':
iris = load_iris()
X,y = create_data()
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
#print(X_train,X_test,y_train,y_test)
clf = DecisionTreeClassifier(criterion='gini',max_depth=4)
print(clf.fit(X_train,y_train,))
print(clf.score(X_test,y_test))
graph = Source(tree.export_graphviz(clf, out_file=None))
graph.format = 'png'
graph.render('dt', view=True)
- 对鸢尾花数据进行预测

- 鸢尾花决策树的结构
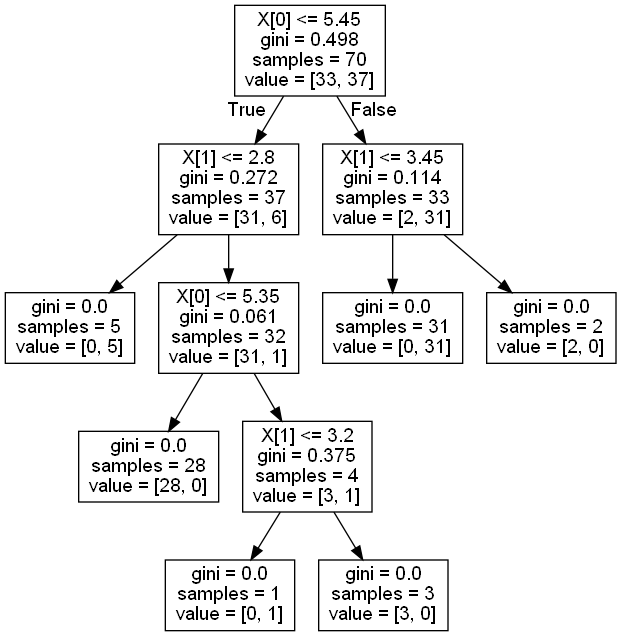
实验小结
- 讨论ID3,C4.5的算法的应用场景
ID3算法应用场景:
他的基础理论清晰,算法比较简单,学习能力较强,适合处理大规模的学习问题,是数据挖掘和知识发现领域中的一个很好的范例,为后来各学者提出优化算法奠定了理论基础,ID3算法特别在机器学、知识发现和数据挖掘等领域得到了极大地发展。
C4.5算法应用案例:
C4.5算法具有条例清晰,能处理连续型属性,防止过拟合,准确性较高和使用范围广等优点,是一个很有使用价值的决策树算法,可以用来分类也可以用来回归。C4.5算法在机器学习,知识发现,金融分析,遥感影响1分类,生产制造、分析生物学和数据挖掘等领域得到广泛应用。 - 分析决策树剪枝策略
- 如何进行决策树剪枝
先对数据集划分成训练集和验证集,训练集用来决定书生成过程中每个节点划分选择的属性,验证集在预剪枝中用于决定该节点是否有必要一句改属性进行展开,在后剪枝中用于判断该节点是否需要进行剪枝。先剪枝(pruning)的目的是为了避免决策树模型的过拟合。因为决策树算法在学习的过程中为了尽可能的正确的分类训练样本,不停地对结点进行划分,因此这会导致整棵树的分支过多,也就导致了过拟合。决策树的剪枝策略最基本的有两种:预剪枝(pre-pruning)和后剪枝(post-pruning): - 预剪枝(pre-pruning):预剪枝就是在构造决策树的过程中,先对每个结点在划分前进行估计,若果当前结点的划分不能带来决策树模型泛华性能的提升,则不对当前结点进行划分并且将当前结点标记为叶结点
预剪枝
- 如何进行决策树剪枝
通过提前停止树的构建而对树剪枝,一旦停止,节点就是树叶,该树叶持有子集元祖最频繁的类。
停止决策树生长最简单的方法有:
1.定义一个高度,当决策树达到该高度时就停止决策树的生长
2.达到某个节点的实例具有相同的特征向量,及时这些实例不属于同一类,也可以停止决策树的生长。这个方法对于处理
数据的数据冲突问题比较有效。
3.定义一个阈值,当达到某个节点的实例个数小于阈值时就可以停止决策树的生长
4.定义一个阈值,通过计算每次扩张对系统性能的增益,并比较增益值与该阈值大小来决定是否停止决策树的生长。
3后剪枝(post-pruning):后剪枝就是先把整颗决策树构造完毕,然后自底向上的对非叶结点进行考察,若将该结点对应的子树换为叶结点能够带来泛华性能的提升,则把该子树替换为叶结点。
Reduced-Error Pruning(REP,错误率降低剪枝)
Pesimistic-Error Pruning(PEP,悲观错误剪枝)
Cost-Complexity Pruning(CCP,代价复杂度剪枝)
EBP(Error-Based Pruning)(基于错误的剪枝)
tips 经验熵



