实验三：朴素贝叶斯算法实验
实验三：朴素贝叶斯算法实验
| 20大数据三班 | 博客班级 | qiao_px |
|---|---|---|
| 学号 | 201613336 | 博客链接 |
【实验目的】
理解朴素贝叶斯算法原理，掌握朴素贝叶斯算法框架。
【实验内容】
- 针对下表中的数据，编写python程序实现朴素贝叶斯算法（不使用sklearn包），对输入数据进行预测；
- 熟悉sklearn库中的朴素贝叶斯算法，使用sklearn包编写朴素贝叶斯算法程序，对输入数据进行预测；
【实验报告要求】
- 对照实验内容，撰写实验过程、算法及测试结果；
- 代码规范化：命名规则、注释；
- 查阅文献，讨论朴素贝叶斯算法的应用场景。
问题一的解决方案
- 不使用sklearn对实现朴素贝叶斯分类
#author:qiao_px
#@Time 2022/11/7 15:34
#@File 贝叶斯.py
import numpy as np
"""
load_data_set():
功能：载入数据集
输入：无
返回：
posting_list：数据集；（西瓜数据集3.0 ； 西瓜书p84中间图表格）
classes_list：各属性的类别
property_list：各个属性的属性值集合列表
"""
def load_data_set():
# 西瓜数据集3.0 西瓜书p84中间图表格
posting_list = [
# 色泽 根蒂 敲声 纹理 脐部 触感 密度 含糖率 好瓜
['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '0.697', '0.460', 'YES'],
['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '0.774', '0.376', 'YES'],
['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '0.634', '0.264', 'YES'],
['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '0.608', '0.318', 'YES'],
['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '0.556', '0.215', 'YES'],
['青绿', '稍缩', '浊响', '清晰', '稍陷', '软粘', '0.403', '0.237', 'YES'],
['乌黑', '稍缩', '浊响', '清晰', '稍陷', '软粘', '0.481', '0.149', 'YES'],
['乌黑', '稍缩', '浊响', '清晰', '稍陷', '硬滑', '0.437', '0.211', 'YES'],
['乌黑', '稍缩', '沉闷', '稍糊', '稍凹', '硬滑', '0.666', '0.091', 'NO'],
['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '0.243', '0.267', 'NO'],
['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '0.245', '0.057', 'NO'],
['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '0.343', '0.099', 'NO'],
['青绿', '稍缩', '浊响', '稍糊', '凹陷', '硬滑', '0.639', '0.161', 'NO'],
['浅白', '稍缩', '沉闷', '稍糊', '凹陷', '硬滑', '0.657', '0.198', 'NO'],
['乌黑', '稍缩', '浊响', '清晰', '稍凹', '软粘', '0.360', '0.370', 'NO'],
['浅白', '蜷缩', '浊响', '模糊', '稍陷', '硬滑', '0.593', '0.042', 'NO'],
['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '0.719', '0.103', 'NO']]
# 各属性值对应的属性列表，未用到
classes_list = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感', '密度', '含糖率', '好瓜']
# 各个属性的属性值集合列表
property_list = [
'青绿', '乌黑', '浅白',
'蜷缩', '稍缩', '硬挺',
'浊响', '沉闷', '清脆',
'清晰', '稍糊', '模糊',
'凹陷', '稍陷', '稍凹',
'硬滑', '软粘']
return posting_list, property_list
"""
getNums(posting_list,col,rows,nums):
功能：取值函数，从数据集中取出某一列（密度或者含糖率样本）多行的值，返回一维数组，及其长度
输入：posting_list：数据集；col：所取数据集的列号；rows:所取数据集的开始行号；nums：取的数据行数；
输出：Nums：浮点型数据列表
"""
def getNums(posting_list, col, rows, nums):
Nums = [0] * nums
for n in range(0, nums):
Nums[n] = float(posting_list[rows + n][col])
return Nums
"""
train_naive_bayes(posting_list,property_list):
功能：训练数据，即计算数据集的类条件概率，类先验概率
输入：posting_list：数据集；property_list：各个属性的属性值集合构成的列表
输出：propertyConditionalProbabilityPositive：正样本(好瓜)类条件概率
propertyConditionalProbabilityNegative：负样本类条件概率
"""
def train_naive_bayes(posting_list, property_list):
# 总的样本数目
trainNum = len(posting_list)
# 正样本数目
pSampleNum = 0
for sample in posting_list:
if sample[-1] == 'YES':
pSampleNum += 1
# 类先验概率
prioClass = pSampleNum / trainNum
# 存储正样本类条件概率
propertyConditionalProbabilityPositive = []
propertyConditionalProbabilityNegative = []
# 通过遍历各个属性的属性值集合列表来求其属于 正/负样本的类条件概率，property_list含所有的属性值（无含糖率和密度）
for propertyy in property_list:
# 拉普拉斯平滑，防止为0,
# 触感属性只有两个值：硬滑和软粘；拉普拉斯平滑时，该属性正/负样本数目即分母加2，其他属性正/负样本数目即其分母加3
if (propertyy == "硬滑") or (propertyy == "软粘"):
pSampleNumLap = pSampleNum + 2
nSampleNumLap = trainNum - pSampleNum + 2
else:
pSampleNumLap = pSampleNum + 3
nSampleNumLap = trainNum - pSampleNum + 3
# 拉普拉斯平滑，初始化为1
posNumPropertyPositive = 1
negNumPropertyPositive = 1
# 遍历数据集的每一个样本
for rows in range(0, len(posting_list)):
# 如果此时的属性值在样本中
if propertyy in posting_list[rows]:
# 如果该样本为正样本
if posting_list[rows][-1] == 'YES':
# 计算此属性值的正样本数目
posNumPropertyPositive += 1
else:
# 计算此属性值的负样本数目
negNumPropertyPositive += 1
# 计算此属性值的正/负类条件概率
propertyConditionalProbabilityPositive.append(posNumPropertyPositive / pSampleNumLap)
propertyConditionalProbabilityNegative.append(negNumPropertyPositive / nSampleNumLap)
# 最后计算正/负样本的 密度和含糖率 的均值和标准差，添加到类条件概率的后面。为了后续通过概率密度函数计算概率
propertyConditionalProbabilityPositive.append(np.mean(getNums(posting_list, 6, 0, pSampleNum)))
propertyConditionalProbabilityPositive.append(np.var(getNums(posting_list, 6, 0, pSampleNum)) ** (1 / 2))
propertyConditionalProbabilityNegative.append(np.mean(getNums(posting_list, 6, pSampleNum, trainNum - pSampleNum)))
propertyConditionalProbabilityNegative.append(
np.var(getNums(posting_list, 6, pSampleNum, trainNum - pSampleNum)) ** (1 / 2))
propertyConditionalProbabilityPositive.append(np.mean(getNums(posting_list, 7, 0, pSampleNum)))
propertyConditionalProbabilityPositive.append(np.var(getNums(posting_list, 7, 0, pSampleNum)) ** (1 / 2))
propertyConditionalProbabilityNegative.append(np.mean(getNums(posting_list, 7, pSampleNum, trainNum - pSampleNum)))
propertyConditionalProbabilityNegative.append(
np.var(getNums(posting_list, 7, pSampleNum, trainNum - pSampleNum)) ** (1 / 2))
# 方差标准差装进类条件概率列表中，大致如下:
# [青绿的正类条件概率,乌黑的正类条件概率,浅白的正类条件概率,蜷缩的正类条件概率,'稍缩的正类条件概率,硬挺的正类条件概率,
# 浊响的正类条件概率,沉闷的正类条件概率,清脆的正类条件概率,清晰的正类条件概率,稍糊的正类条件概率,模糊的正类条件概率,
# 凹陷的正类条件概率,稍陷的正类条件概率,稍凹的正类条件概率,硬滑的正类条件概率,软粘的正类条件概率,
# 正类别的密度的均值,正类别的密度方差,
# 正类别的含糖率均值，正类别的含糖率方差]
return propertyConditionalProbabilityPositive, propertyConditionalProbabilityNegative
"""
classify_naive_bayes(data,propertyConditionalProbabilityPositive,property_list,propertyConditionalProbabilityNegative):
功能：求正负类别的概率，返回1或者0， 1表示为正样本
输入：data：想要测试的数据，格式见底部说明。propertyConditionalProbabilityPositive正类条件概率；propertyConditionalProbabilityNegative负类条件概率
输出：返回1或者0；其中1代表正样本（好瓜），0代表负样本
"""
def classify_naive_bayes(data, propertyConditionalProbabilityPositive, property_list,
propertyConditionalProbabilityNegative):
probabilityPos = 0
probabilityNeg = 0
# 遍历测试数据的属性， 其密度和含糖率不在循环中计算
for propertyData in data[:-1]:
if propertyData in property_list:
# 取该属性的下标
index = property_list.index(propertyData)
# 取该属性值的正/负样本类条件概率 值，并取对数，然后加起来来求正负样本各自的概率。 取对数为了防止下溢，将乘法转为加法计算。
probabilityPos += np.log(propertyConditionalProbabilityPositive[index])
probabilityNeg += np.log(propertyConditionalProbabilityNegative[index])
# 对于连续属性密度和含糖率，通过概率密度函数计算其属于正/负样本的概率。
probabilityPos += np.log(((2 * np.pi) ** (-1 / 2) * propertyConditionalProbabilityPositive[-4]) ** (-1)) + (
-1 / 2) * ((float(data[-2]) - propertyConditionalProbabilityPositive[-4]) ** 2) / (
propertyConditionalProbabilityPositive[-3] ** 2)
probabilityPos += np.log(((2 * np.pi) ** (-1 / 2) * propertyConditionalProbabilityPositive[-2]) ** (-1)) + (
-1 / 2) * ((float(data[-1]) - propertyConditionalProbabilityPositive[-2]) ** 2) / (
propertyConditionalProbabilityPositive[-1] ** 2)
probabilityNeg += np.log(((2 * np.pi) ** (-1 / 2) * propertyConditionalProbabilityNegative[-4]) ** (-1)) + (
-1 / 2) * ((float(data[-2]) - propertyConditionalProbabilityNegative[-4]) ** 2) / (
propertyConditionalProbabilityNegative[-3] ** 2)
probabilityNeg += np.log(((2 * np.pi) ** (-1 / 2) * propertyConditionalProbabilityNegative[-2]) ** (-1)) + (
-1 / 2) * ((float(data[-1]) - propertyConditionalProbabilityNegative[-2]) ** 2) / (
propertyConditionalProbabilityNegative[-1] ** 2)
# 对算出来的正负概率进行比较，大的为正样本
if probabilityPos > probabilityNeg:
return True
else:
return False
if __name__ == "__main__":
# 载入数据
posting_list, property_list = load_data_set()
# 预训练
propertyConditionalProbabilityPositive, propertyConditionalProbabilityNegative = train_naive_bayes(posting_list,
property_list)
# 朴素贝叶斯求类别
# 输入数据集中前两个负样本例子
data = ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '0.697', '0.460']
result = classify_naive_bayes(data, propertyConditionalProbabilityPositive, property_list,
propertyConditionalProbabilityNegative)
print('好瓜: {}'.format(result))
data = ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '0.774', '0.376']
result = classify_naive_bayes(data, propertyConditionalProbabilityPositive, property_list,
propertyConditionalProbabilityNegative)
print('好瓜: {}'.format(result))
# 输入数据集中前两个负样本例子
data = ['乌黑', '稍缩', '沉闷', '稍糊', '稍凹', '硬滑', '0.666', '0.091']
result = classify_naive_bayes(data, propertyConditionalProbabilityPositive, property_list,
propertyConditionalProbabilityNegative)
print('好瓜 : {}'.format(result))
data = ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '0.243', '0.267']
result = classify_naive_bayes(data, propertyConditionalProbabilityPositive, property_list,
propertyConditionalProbabilityNegative)
print('好瓜:{}'.format(result))
# 西瓜书p151 列子
data = ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '0.697', '0.460']
result = classify_naive_bayes(data, propertyConditionalProbabilityPositive, property_list,
propertyConditionalProbabilityNegative)
print('好瓜:{}'.format(result))
# 输入data的 格式：
# 如 ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '0.697','0.460']
# 每个属性类别及其可选范围如下：
# 色泽: '青绿','乌黑','浅白',
# 根蒂: '蜷缩','稍缩','硬挺',
# 敲声: '浊响','沉闷','清脆',
# 纹理: '清晰','稍糊','模糊',
# 脐部: '凹陷','稍陷','稍凹',
# 触感: '硬滑','软粘'
# 密度: (0,1)
# 含糖率: (0,1)
预测结果：
问题二的解决方案：
- 使用sklearn实现朴素贝叶斯分类
`
#author:qiao_px
#@Time 2022/11/7 15:45
#@File 贝叶斯sklearn.py
import warnings
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import BernoulliNB
import pandas as pd
warnings.filterwarnings('ignore')
def load_data_set():
# 西瓜数据集3.0 西瓜书p84中间图表格
posting_list = [
#色泽 【青绿、乌黑、浅白】
#根蒂【蜷缩、稍缩、硬挺】
#敲声【清晰、稍糊,、模糊】
# 色泽 根蒂 敲声 纹理 脐部 触感 密度 含糖率 好瓜
[0, 0, 0, 0, 0, 0, '0.697', '0.460', 1],
[1, 0, 1, 0, 0, 0, '0.774', '0.376', 1],
[1, 0, 0, 0, 0, 0, '0.634', '0.264', 1],
[0, 0, 1, 0, 0, 0, '0.608', '0.318', 1],
[2, 0, 0, 0, 0, 0, '0.556', '0.215', 1],
[0, 1, 0, 0, 1, 1, '0.403', '0.237', 1],
[1, 1, 0, 0, 1, 1, '0.481', '0.149', 1],
[1, 1, 0, 0, 1, 0, '0.437', '0.211', 1],
[1, 1, 1, 1, 2, 0, '0.666', '0.091', 0],
[0, 2, 2, 0, 3, 1, '0.243', '0.267', 0],
[2, 2, 2, 2, 3, 0, '0.245', '0.057', 0],
[2, 0, 0, 2, 3, 1, '0.343', '0.099', 0],
[0,1, 0, 1, 0, 0, '0.639', '0.161', 0],
[2, 1, 1, 1, 0, 0, '0.657', '0.198', 0],
[1, 1, 0, 0, 2, 1, '0.360', '0.370', 0],
[2, 0, 0, 2, 1, 0, '0.593', '0.042', 0],
[0, 0, 1, 1, 2, 0, '0.719', '0.103', 0]]
# 各属性值对应的属性列表，未用到
classes_list = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感', '密度', '含糖率', '好瓜']
# 各个属性的属性值集合列表
property_list = [
'青绿', '乌黑', '浅白',
'蜷缩', '稍缩', '硬挺',
0, 1, 2,
0, 1, 2,
0, 1, 2,
0, 1]
return posting_list, property_list
if __name__ == '__main__':
data,result = load_data_set()
data1 = np.array(data,dtype='float32')
#data2= data1[:,0:8]
#target = data1[:,8:]
target = np.array([0,1,2,3,4,5,6,7,8],dtype='float32')
print("data:{},result:{},type:{}".format(data1,result,data1.dtype))
#数据处理
# columns = ['色泽','根蒂','敲声','纹理','脐部','触感','密度','含糖率','好瓜']
# dataDF = pd.DataFrame(data)
# dataDF.columns = columns
# print(dataDF)
# dataDF.to_csv("./xoguashu.csv",encoding='gbk',index=False)
Xtrain, Xtest, Ytrain, Ytest = train_test_split(data1.T, target, test_size=0.3, random_state=420)
clf = BernoulliNB()
clf.fit(data1.T,target)
# 实例化和训练训练集
#gnb = BernoulliNB().fit(Xtrain, Ytrain)
# 查看分数
acc_score = clf.score(Xtest, Ytest) # 返回预测的精确性
# 查看预测结果
Y_pred = clf.predict(Xtest)
查看预测结果
分数：
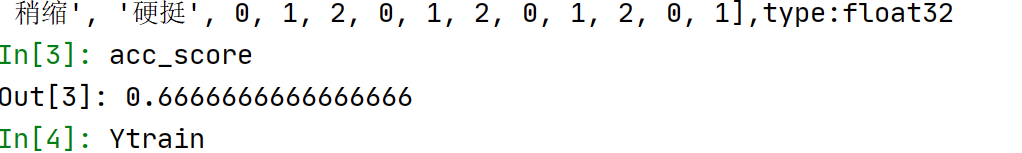
查看测试集的预测结果
