树状数组
树状数组
基本原理如下图所示
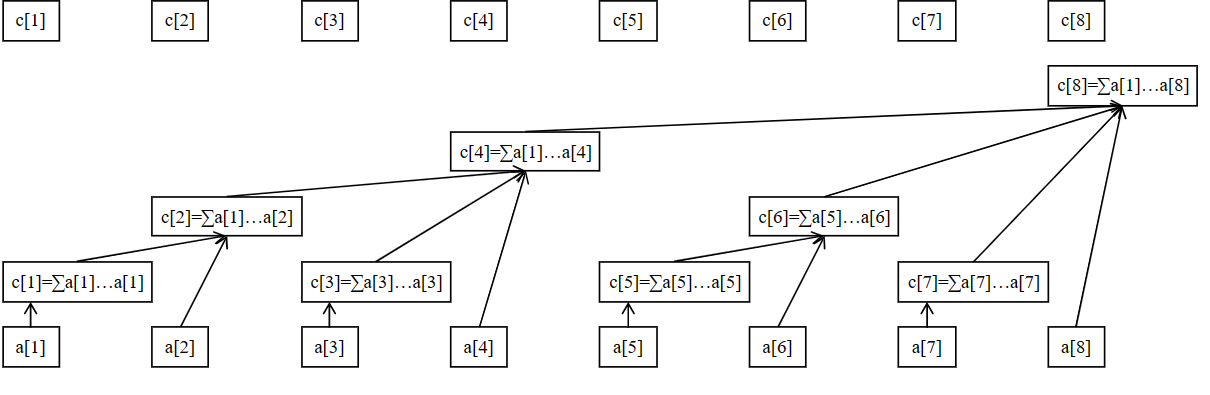
树状数组支持单点修改、区间查询等操作
由原数组\(a[x]\)转换为数组\(c[x]\)，我们可以知道，对于c数组的每一个x，其所管辖的范围就是\([x-lowbit(x)+1,x]\)，长度为\(2^k\)，其中 k 恰好为 x 二进制表示中，最低位的 1 所在的二进制位数，\(2^k\)为恰好为 x 二进制表示中，最低位的 1 以及后面所有 0 组成的数。
举个栗子：\(c_{88}\)管辖哪个区间？
\((88)_{10}=(01011000)_2\)，其二进制最低位的1以及后面的0组成的二进制是\(1000\)，即 8，所以\(c_{88}\)管辖 8 个 a 数组中的元素，区间为\([81,88]\)。
那么问题来了，\(lowbit(x)\)怎么求？
int lowbit(int x){
return x&(-x);
}
板子
板子
struct BIT{
int num;
vector<ll> c;
BIT(int x) : num(x), c(x + 1, 0) {}
int lowbit(int x){ return x & (-x); }
void update(int x, ll v){// 单点修改
while(x <= num){
c[x] += v;
x += lowbit(x);
}
return ;
}
void update(int l, int r, ll v){// 差分，[l, r]区间修改
if(l > r) return ;
update(l, v);
update(r + 1, - v);
return ;
}
ll query(int x){
ll res = 0;
while(x){
res += c[x];
x -= lowbit(x);
}
return res;
}
ll query(int l, int r){
return query(r) - query(l - 1);
}
};
建树
怎么由原数组\(a[x]\)转换为数组\(c[x]\)？
目前学会了一种方法
- 前缀和法求c[x]
for(int i=1;i<=n;++i){
c[i]=qz[i]-qz[i-lowbit(i)];
}
之后就是应用lowbit(x)，对所给a[x]进行维护
- 利用单点修改建树
单点修改、区间查询
下面给出代码：
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
const ll maxm=1e6+5,mod=1e9+7;
ll c[maxm],a[maxm],n,q,qz[maxm];
int lowbit(int x){
return x&(-x);
}
ll getsum(ll x){//区间查询
ll ans=0;
while(x>0){
ans=ans+c[x];
x=x-lowbit(x);
}
return ans;
}
void update(int x,int v){//单点修改
while(x<=n){
c[x]+=v;
x=x+lowbit(x);
}
return ;
}
void pre(){
for(int i=1;i<=n;++i){
c[i]=qz[i]-qz[i-lowbit(i)];
}
return ;
}
void solve(){
cin>>n>>q;
for(int i=1;i<=n;++i){
cin>>a[i];
qz[i]+=qz[i-1]+a[i];
}
pre();
ll a,c,x;
while(q--){
cin>>a>>c>>x;
if(a==1){
update(c,x);
}else{
cout<<getsum(x)-getsum(c-1)<<"\n";
}
}
return ;
}
signed main(){
int _=1;
// cin>>_;
while(_--){
solve();
}
return 0;
}
2.https://www.luogu.com.cn/problem/P3374
树状数组模板题，单点修改，区间查询
区间修改，单点查询
利用树状数组维护差分数组，实现区间修改，单点查询
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
const ll maxm=1e6+5,mod=1e9+7;
ll c[maxm],a[maxm],n,q,qz[maxm];
int lowbit(int x){
return x&(-x);
}
ll getsum(ll x){
ll ans=0;
while(x>0){
ans=ans+c[x];
x=x-lowbit(x);
}
return ans;
}
void update(int x,int v){//保持单点修改的update
while(x<=n){
c[x]+=v;
x=x+lowbit(x);
}
return ;
}
void pre(){
for(int i=1;i<=n;++i){
c[i]=qz[i]-qz[i-lowbit(i)];//依旧是利用前缀和建树
}
return ;
}
void solve(){
cin>>n>>q;
for(int i=1;i<=n;++i){
cin>>a[i];
qz[i]+=qz[i-1]+a[i]-a[i-1];//前缀和数组为a的差分数组的前缀和数组
}
pre();
ll c,l,r,x;
while(q--){
cin>>c;
if(c==1){
cin>>l>>r>>x;
update(l,x);//区间修改两步
update(r+1,-x);
}else{
cin>>x;
cout<<getsum(x)<<'\n';
}
}
return ;
}
signed main(){
int _=1;
// cin>>_;
while(_--){
solve();
}
return 0;
}
区间修改，区间查询
在区间修改，单点查询的基础上实现区间查询
最直接的，我们要快捷实现区间查询，就是要在上面实现的差分数组快速的求前缀和，简单的再开一个树状数组？显然不可能，让我们先找找差分数组前缀和与区间和的关系
位置p的前缀和：\(\sum_{i=1}^{p}{a[i]}=\sum_{i=1}^{p}{\sum_{j=1}^{i}{d[j]}}\)
对于右侧的\(d[j]\)加以分析，可以发现\(d[1]被引用了p次，d[2]被引用了p-1次,...\)，那么我们可以写出：
位置p的前缀和：\(\sum_{i=1}^{p}{\sum_{j=1}^{i}{d[j]}}=\sum_{i=1}^{p}{d[i]*(p-i+1)}=(p+1)*\sum_{i=1}^{p}{d[i]}-\sum_{i=1}^{p}{d[i]}*i\)
那么我们可以维护两个数组的前缀和：
一个数组是\(sum1[i]=\sum d[i]\)，
另一个数组是\(sum2[i]=\sum i*d[i]\)
对于要求的两大操作
查询
位置p的前缀和即： (p + 1) * sum1数组中p的前缀和 - sum2数组中p的前缀和。
区间 [l, r] 的和即：位置 r 的前缀和 - 位置 l 的前缀和。
修改
对于sum1数组的修改同问题2中对d数组的修改
对于sum2数组的修改也类似，我们给 sum2[l] 加上 l * x，给 sum2[r + 1] 减去 (r + 1) * x
例题：
看到这如果你问为什么没有单点修改，单点查询啊？
sorry，这个这么简单，你拍拍脑袋就知道，数组都支持这个操作了！
其他拓展内容
求解全局逆序对问题
详见本篇随笔
