相关性分析

什么是相关性分析：

相关性分析研究现象之间是否存在某种依存关系，对具体有依存关系的现象探讨相关方向及相关程度。

相关分析是一种简单易行的测量定量数据之间的关系情况的分析方法。可以分析包括变量间的关系情况以及关系强弱程度等

有点类似于特征提取

常用的相关性分析方法

协方差及协方差矩阵

协方差用来衡量两个变量的总体误差，如果两个变量的变化趋势一致，协方差就是正值，说明两个变量正相关。如果两个变量的变化趋势相反，协方差就是负值，说明两个变量负相关。如果两个变量相互独立，那么协方差就是0，说明两个变量不相关。协方差只能对两组数据进行相关性分析，当有两组以上数据时就需要使用协方差矩阵。

协方差通过数字衡量变量间的相关性，正值表示正相关，负值表示负相关。但无法对相关的密切程度进行度量。当我们面对多个变量时，无法通过协方差来说明那两组数据的相关性最高。要衡量和对比相关性的密切程度，就需要使用下一个方法：相关系数

相关系数

相关系数(Correlation coefficient)是反应变量之间关系密切程度的统计指标，相关系数的取值区间在1到-1之间。1表示两个变量完全线性相关，-1表示两个变量完全负相关，0表示两个变量不相关。数据越趋近于0表示相关关系越弱。

 

person correlation coefficient（皮尔森相关性系数）

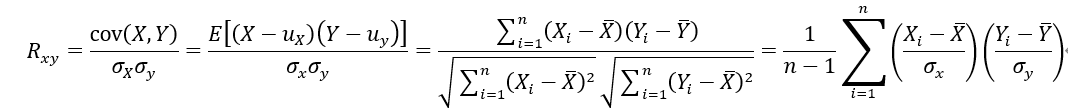
其中Rxy表示样本相关系数，cov（x,y）表示样本协方差，Sx表示X的样本标准差，Sy表示y的样本标准差。用于度量两个变量X和Y之间的相关（线性相关）

spearman correlation coefficient（斯皮尔曼相关性系数）

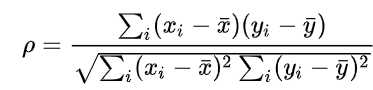
它是衡量两个变量的依赖性的 非参数 指标。 

kendall correlation coefficient（肯德尔相关性系数）

回归分析->一元和多元

回归分析（regression analysis)是确定两组或两组以上变量间关系的统计方法。回归分析按照变量的数量分为一元回归和多元回归。两个变量使用一元回归，两个以上变量使用多元回归。进行回归分析之前有两个准备工作，第一确定变量的数量。第二确定自变量和因变量。

回归分析法的步骤如下：

1、根据自变量与因变量的现有数据以及关系，初步设定回归方程；

2、求出合理的回归系数；

3、进行相关性检验，确定相关系数；

4、在符合相关性要求后，即可根据已得的回归方程与具体条件相结合，来确定事物的未来状况，并计算预测值的置信区间。

偏相关分析

偏相关分析是指当两个变量同时与第三个变量相关时，将第三个变量的影响剔除，只分析另外两个变量之间相关程度的过程，判定指标是相关系数的R值。

p值是针对原假设H0：假设两变量无线性相关而言的。一般假设检验的显著性水平为0.05，你只需要拿p值和0.05进行比较：如果p值小于0.05，就拒绝原假设H0，说明两变量有线性相关的关系，他们无线性相关的可能性小于0.05；如果大于0.05，则一般认为无线性相关关系，至于相关的程度则要看相关系数R值，R越大，说明越相关。越小，则相关程度越低。偏相关分析也称净相关分析，它在控制其他变量的线性影响的条件下分析两变量间的线性相关性，所采用的工具是偏相关系数（净相关系数）。控制变量个数为一时，偏相关系数称为一阶偏相关系数；控制变量个数为二时，偏相关系数称为二阶相关系数；控制变量个数为为零时，偏相关系数称为零阶偏相关系数，也就是相关系数