多指手抓取静力学及抓取约束与特性
多指手,或者说灵巧手,往简单来说是由n台机械臂通过协同合作来完成特定任务的一种耦合系统。只不过这里的机械臂为了极大的缩小体积,选用了微型驱动装置或者说是将驱动装置外置的方式。
多指手抓取分为强力抓取(power grasp,或称手掌抓取)和精确抓取(precision grasp,或称指尖抓取),强力抓取情况下运动和力的分析控制相比于精确抓取更加复杂,所以这里只讨论精确抓取的静力学,即指尖与物体表面接触的情况。
Ⅰ. 静力学坐标系定义
和机械臂坐标系定义类似,整个系统包括全局坐标系  、关节坐标系,另外定义了手指基坐标系
、关节坐标系,另外定义了手指基坐标系  、指尖坐标系
、指尖坐标系  、物体接触坐标系
、物体接触坐标系  、手指接触坐标系
、手指接触坐标系  ,物体坐标系
,物体坐标系  。
。
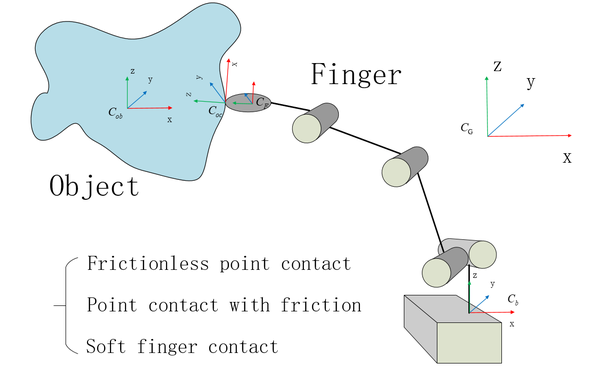
其中物体接触坐标系  和手指接触坐标系
和手指接触坐标系  以手指和物体的接触点为原点,以物体表面接触点的内法线方向为Z轴方向。
以手指和物体的接触点为原点,以物体表面接触点的内法线方向为Z轴方向。
Ⅱ. 手指与物体的接触模型
以下各式中  均表示广义接触力。
均表示广义接触力。
-
无摩擦点接触(Frictionless point contact)
该模型描述的接触关系中,物体与手指只接触于一点,且该点不存在摩擦力,只存在法向力,所以这个力在除z轴外的其它五个维度全为零。
-
摩擦点接触(Point contact with friction)
该模型描述的接触关系中,物体与手指只接触于一点,且该点存在摩擦力和法向力,摩擦力方向为沿物体接触表面切线方向,此时接触力必须在以表面法线为轴线的摩擦锥内才能保证手指与物体的稳定接触。摩擦角由摩擦系数  决定。
决定。
-
软手指接触(Soft finger contact)
顾名思义,该情况下接触不再是一个点,而是一个面,多个点受力必然会产生沿法线方向的力矩,此时接触力就扩展到了四维。另外涉及到力矩摩擦系数 
Ⅲ. 抓取映射矩阵
多指抓取情况下,手指与物体之间的接触力与物体所受合力之间的映射关系可以由抓取矩阵  来表示,
来表示,  ,k为手指个数,
,k为手指个数,  是第i个手指与物体间接触向量的维数,p在三维空间自然是6。
是第i个手指与物体间接触向量的维数,p在三维空间自然是6。
于是有
其中
Ⅳ. 抓取约束与特性
在接触不打滑即接触稳定的情况下,由物体和手指在接触点处相对于物体接触坐标系的速度相同即可得出:
上式中各符号分表表示雅可比矩阵,关节角速度,抓取矩阵的转置以及物体位姿的微分。因此在多指抓取系统中,  和
和  完全反映了抓取物体的特性。
完全反映了抓取物体的特性。
为了满足抓取的力封闭性,我们需要使得加在手指上的力的合力能够完全抵消物体所受的外力,得到合力然后由抓取映射矩阵从物体空间反映射到接触空间,最后由雅可比矩阵将外力内推,从接触空间反映射到关节空间,然后由执行机构执行到相应的运动学参数目标。
以上是力/力矩域,在速度域上反推即可。
ⅴ. 如何保证抓取的稳定
稳定抓取可以通过形封闭和力封闭来满足,形封闭顾名思义,力封闭概念如下:
-
力封闭性
对于施加在物体上的任意外力  ,如果存在多指手能够产生接触力
,如果存在多指手能够产生接触力  使得
使得
则称该抓取满足力封闭。另外还有内力和严格内力的概念,即物体上合力为零的接触力的集合,如果内力在摩擦锥内部则成为严格内力。内力是抓取矩阵的零空间与接触力集合的元素。
-
可操作性
若多指手抓取过程中物体任意运动都不会脱离,则该抓取是可操作的,在形位 ) 下,若多指手一直能满足条件
下,若多指手一直能满足条件
则抓取在形位) 可操作,换句话说就是,雅可比矩阵的值域空间包含于抓取映射矩阵的转置的值域空间。
可操作,换句话说就是,雅可比矩阵的值域空间包含于抓取映射矩阵的转置的值域空间。
分类:
【2】多指灵巧手/假手理论







【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 如何调用 DeepSeek 的自然语言处理 API 接口并集成到在线客服系统
· 【译】Visual Studio 中新的强大生产力特性
· 2025年我用 Compose 写了一个 Todo App