TS 类型编程终极优化：递归、尾递归、递归的递归

公告

本文章所有代码均已验证可在 TS v4.8.4 版本到 v5.0.4 版本成功运行，但是 v5.0.4 版本以上还没验证

本人语言较为跳脱，阅读本文章可能需要一定类型编程基础

最近在沉迷 TS 类型编程，追求极致性能。知道有个叫尾递归的东西可以提高递归层数。但是实际一试，还是有限制，最多 $1000$ 层。
如何在递归层数不变的情况下完成做出更多动作呢？且听我娓娓道来……

普通的递归

这里我们就用“生成特定长度的字符串字面量类型”来举例。

之所以不用元组而用字符串，是因为目前本人使用 VSCode 中 TS v4.9.4 环境下元组最多是 $9999$ 元素。再多的话编辑器就会报 ts(2799) 错误：“类型生成的元组类型太大，无法表示。”
至于为什么不是编译期间报错，因为本人自己在电脑上编译时还没报错就已经 out of memory 了。大概也有可能跟电脑性能有关系。

如何生成特定长度的字符串呢？这句话可以分成两部分：

首先是如何“特定长度”。
基本上我们可以使用两种方法来表示长度：

使用数字表示长度。当然在 TS 类型编程的世界里不支持直接进行数字运算，所以可以先不用考虑这方法。
使用一个特定长度的字符串或元组。通过 infer 来逐渐缩短他们的长度，他们的长度便决定了迭代的次数。

然后是如何“生成字符串字面量类型”。
这里我们可以使用“模板”进行字符串之间的拼接。

这里就生成一个全是 Z 的字符串吧。

type Gened<A extends string>
  = (A extends `${any}${infer A}`
    ? `Z${Gened<A>}`
    : ''
  );

这是一个很平常的实现，可以生成与所给字符串字面量类型 A 长度相等的字符串。

我们来用五十铃测试一下：

type A = Gened<`${''
  }${'00000000000000000000000000000000000000000000000000'
  }`>;

然后我们发现只放了一条就炸了。报的是 ts(2589) 错误：“类型实例化过深，且可能无限。” 删两个 0 就发现不报错了。看来最多生成 $48$ 个字符了。

由于就算只剩一个字符也符合模板字符串的条件（那单独的一个字符算作 `${any}${infer A}` 中的 ${any}，而 infer 得到的 A 是空字符串），从而让 infer 出来的空字符串也被迭代一次（这次迭代就不匹配 extends 了，所以这次才算作最后一次），再用一层栈空间，所以 ${栈空间} = {字数} + 1$ 。由此可以推断出 TS 递归基本上最多是 $48 + 1 = 49$ 层了。

有意思的是，如果你在 A 前面再加一个 HH 类型，就像这样：
type HH = Gened<'00000000'>;
type A = Gened<`${''
  }${'00000000000000000000000000000000000000000000000000'
  }`>;
那么类型 A 就不会爆掉了。这可能是因为 TypeScript 会记忆化相同的输入。

尾递归大法好啊，那么使用尾递归呢？

尾递归

type Gened<
  A extends string,
  R extends string = '',
>
  = (A extends `${any}${infer A}`
    ? Gened<A, `${R}Z`>
    : R
  );

这里我们使用多出来的一个类型参数 R 来保存之前得到的结果，实现尾递归。
于是再请出我们的五十铃小姐：

type A = Gened<`${''
  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'

  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'

  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'

  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'

  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'
  }${'00000000000000000000000000000000000000000000000000'
  }`>

一般情况下，到这里的时候就开始报错了。这是刚好 $1000$ 个 0 的程度。如果你在末尾删掉一个 0，就会发现神奇的不报错了。所以我们验证了，开头说的 $1000$ 尾递归限制。

尾递归可能是我们能想到的最好的优化了。在不增加迭代次数的情况下怎么才能做到生成更长的字符串呢？

一个很好的思路是在一次迭代中生成多个字符串。

暴力堆叠

我们可以在一次迭代中消耗掉所给字符串的多个字符，并生成多个 Z。对于所给字符串太短无法被消耗的情况，我们可以再使用一个一个生成的泛型类型进行精细处理。

这里我让 Gened5 一次生成 $5$ 个字符。而 Gened1 一次只生成 $1$ 个，用来精细处理。

type Gened1<
  A extends string,
  R extends string = ''>
  = (A extends `${any}${infer A}`
    ? Gened1<A, `${R}Z`>
    : R
  )

type Gened5<
  A extends string,
  R extends string = ''>
  = (A extends `${any}${any}${any}${any}${any}${infer A}`
    ? Gened5<A, `${R}ZZZZZ`>
    : Gened1<A, R>
  )

于是再召唤五十铃……咳咳，开玩笑的。
到这一步应该可以发现 Gened5 最多可以生成 $5000 - 10 = 4990$ 个字符——五十铃太多这里放不下。

由此对尾递归的思考

那么为什么是 $4990$ 呢？我们来稍微分析一下。

首先我们知道 Gened5 最多迭代 $1000$ 次。
最后一次必定匹配不了模板字符串，所以最后一次的字符数 $<5$，除最后一次之外的 $999$ 次每次都吃掉了源字符串 $5$ 个字符。
也就是说理论上 Gened5 最多可以吃掉 $999 \times 5 + 4 = 4999$ 个字符。
事实上，如果最后不再套个 Gened1，你会发现确实能吞 $4999$ 个字符。

于是显而易见，少掉的 $9$ 个字符来自末尾对 Gened1 的调用。

在一个类型末尾调用其他类型是否被算作尾递归其实是有点玄学的。
像本例，唯一的解释就是调用 Gened1 会额外占用一层栈空间，那就是不算尾递归。
但是下面这个例子里，相互调用却会被认作尾递归而不会爆栈：

type TypeA<
  A extends string,
  R extends string = ''>
  = (A extends `${any}${infer A}`
    ? TypeB<A, `${R}Z`>
    : R
  )

type TypeB<
  A extends string,
  R extends string = ''>
  = (A extends `${any}${infer A}`
    ? TypeA<A, `${R}Z`>
    : R
  )

// 读者可自行用五十铃尝试一下

总之从工程角度来讲，这些细节不太重要。
只要叠的够多，心理就会踏实一点。

递归的递归

可能有些会偷懒（也就是聪明）的读者发现了：我们何必真的用手输上 $5$ 个字符，来一次生成 $5$ 个字符呢？
考虑到 Gened1 可以在 $999$ 的范围里准确的生成字符，为何我们不用这个类型来代替我们手打呢？
虽然小小的 $5$ 个字符可能有人不放在眼里，但是如果你堆了 $500$ 个呢？$5000$ 个呢？（但是考虑到尾递归的上限，堆 $5000$ 个的话大概这方法也救不了你了）

改造后的代码：

type Gened1<
  A extends string,
  R extends string = ''>
  = (A extends `${any}${infer A}`
    ? Gened1<A, `${R}Z`>
    : R
  )

type Gened5<
  A extends string,
  R extends string = ''>
  = (A extends `${any}${any}${any}${any}${any}${infer A}`
    ? Gened5<A, Gened1<'12345', R>>
    : Gened1<A, R>
  )

呵呵，打眼一瞧……你会发现还是要输 $5$ 个字符当作输入。

但是不要忘了一开始说的：还有一种方法是使用数字做输入表示长度。

“数字化”改造

这里我们可以简单实现一个字符串表示的数字字面量加减法和大小判断。用上尾递归，最大 $997$ 位的数之间的比较/相加/相减还是可以的：

namespace Calc {
  type SigNumber = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
  type SigT = SigNumber | 's'
  type SigVary<T, N> = N extends SigNumber ? (T extends 0 ? [1, 2, 3, 4, 5, 6, 7, 8, 9, 's'] : ['s', 0, 1, 2, 3, 4, 5, 6, 7, 8])[N] : 's'
  type SigCmp<A extends SigT, B extends SigT> = A extends B ? 0 : A extends 's' ? -1 : B extends 's' ? 1 : SigCmp<SigVary<0, A>, SigVary<0, B>>
  type CmpP0<A extends string, B extends string> = `${A},${B}` extends `${infer A0 extends SigNumber}${infer A},${infer B0 extends SigNumber}${infer B}` ? SigCmp<A0, B0> extends infer K extends -1 | 1 ? K : CmpP0<A, B> : 0
  type StrSubedSub<A extends string, B, R extends string> = B extends `${any}${infer B}` ? A extends `${any}${infer A}` ? StrSubedSub<A, B, R> : StrSubedSub<A, B, `${R}Z`> : { r: R, a: A }
  type StrSubed<A extends string, B> = StrSubedSub<A, B, ''> extends { r: infer R } ? R extends '' ? 0 : R : never
  type Filled0<B, R extends string> = B extends `${any}${infer B}` ? Filled0<B, `${R}${0}`> : R
  type PreAligned<A extends string, B> = `${Filled0<StrSubed<A, B>, ''>}${A}`
  type LenCmp<A extends string, B extends string> = PreAligned<A, B> extends A ? PreAligned<B, A> extends B ? 0 : -1 : 1
  type SntCmpUns<A extends string, B extends string> = string extends A | B ? 1 | -1 | 0 : LenCmp<A, B> extends infer K extends -1 | 1 ? K : CmpP0<A, B>
  type SntCmp<A extends string, B extends string> = A extends `-${infer A}` ? B extends `-${infer B}` ? SntCmpUns<B, A> : 1 : B extends `-${any}` ? -1 : SntCmpUns<A, B>
  export type IsNotless<A extends string, B extends string> = { [-1]: true, 0: true, 1: false }[SntCmp<A, B>];
  type Leading0less<N extends string> = N extends `0${infer K}` ? K extends '' ? N : Leading0less<K> : N
  type StringReved<N, R extends string = ''> = N extends `${infer I}${infer S}` ? StringReved<S, `${I}${R}`> : R
  type GotQH<Q = any, H = any> = { q: Q, h: H }
  type SigInfl<T extends 0 | 9, A, B, E extends 1 | 0> = B extends 0 ? A extends 's' ? GotQH<1, T> : GotQH<E, A> : A extends SigNumber ? SigInfl<T, SigVary<T, A>, SigVary<9, B>, E> : SigInfl<T, T, B, 1>
  type SigTrinfl<T extends 0 | 9, A, B, C extends 0 | 1> = SigInfl<T, A, B, 0> extends infer K extends GotQH ? SigInfl<T, K['h'], C, K['q']> : GotQH<0, 0>
  type AosOri<T extends 0 | 9, A extends string, B extends string, J extends 0 | 1, R extends string> = `${A},${B}` extends `${infer A0 extends SigNumber}${infer A},${infer B0 extends SigNumber}${infer B}` ? SigTrinfl<T, A0, B0, J> extends infer S extends GotQH ? AosOri<T, A, B, S['q'], `${R}${S['h']}`> : R : R
  type AosHal<T extends 0 | 9, A extends string, B extends string> = Leading0less<StringReved<AosOri<T, `${StringReved<PreAligned<A, B>>}0`, `${StringReved<PreAligned<B, A>>}0`, 0, ''>>>
  export type Subed<A extends string, B extends string> = AosHal<9, A, B>
}

于是我们的字符生成可以改写成使用字符串形式的数字作为输入的：

type Gened1<
  A extends string,
  R extends string = ''>
  = (Calc.IsNotless<A, '1'> extends true
    ? Gened1<Calc.Subed<A, '1'>, `${R}Z`>
    : R
  )

type Gened5<
  A extends string,
  R extends string = ''>
  = (Calc.IsNotless<A, '5'> extends true
    ? Gened5<Calc.Subed<A, '5'>, Gened1<'5', R>>
    : Gened1<A, R>
  )

type A = Gened5<'2'> // "ZZ"
type B = Gened5<'5'> // "ZZZZZ"

一个比较直观的比喻

我们可以把要生成的字符串比喻成过河的石头，一个字符就是一个石头，我们把这些石头全都踩到就算过了河。

那么这里 Gened1 一次生成 $1$ 个字符，就是一步一步踩着石头过河。

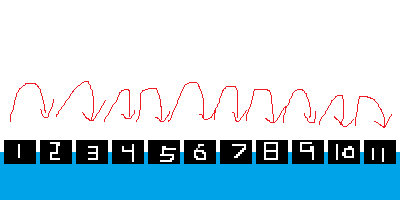
一步一步过河

而 Gened5 一次跳 $5$ 个石头。

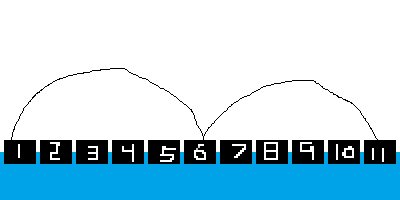
五步五步过河

跳着走就没法踩到全部的石头，于是 Gened5 再拽着 Gened1 帮它去一步一步踩那些没有踩到的石头。

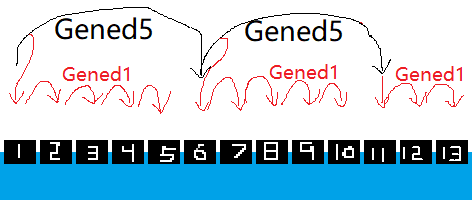
详解五步五步过河

我们可以发现，这个样子的话就会同时出现上面黑色的 Gened5 和下面红色的 Gened1 两条线，所以最多同时占据两层栈空间。

换个角度，我们可以认为这种方法多使用了一层 Gened5 的栈，使得 Gened1 这层栈可以在达到 $1000$ 次尾递归限制之前被回收，然后被重新使用，重新计算尾递归的限次——我们之所以可以让 Gened1 突破 $1000$ 大限，是因为它尾递归了不止一次。

递归着调用尾递归

根据前文，既然 Gened1 可以突破尾递归限制，那么 Gened5 当然也可以。继续下去的 Gened10 或者 Gened100 也都可以。

为了防止爆栈，我们平常在工程中往往会堆的越多越好。一般来说，我会选择先叠 Gened10，然后再叠 Gened100，再叠 Gened1000 ：

type GenedV0<
  A extends string,
  R extends string = ''>
  = (Calc.IsNotless<A, '1'> extends true
    ? GenedV0<Calc.Subed<A, '1'>, `${R}Z`>
    : R
  )

type GenedV1<
  A extends string,
  R extends string = ''>
  = (Calc.IsNotless<A, '10'> extends true
    ? GenedV1<Calc.Subed<A, '10'>, GenedV0<'10', R>>
    : GenedV0<A, R>
  )

type GenedV2<
  A extends string,
  R extends string = ''>
  = (Calc.IsNotless<A, '100'> extends true
    ? GenedV2<Calc.Subed<A, '100'>, GenedV1<'100', R>>
    : GenedV1<A, R>
  )

type GenedV3<
  A extends string,
  R extends string = ''>
  = (Calc.IsNotless<A, '1000'> extends true
    ? GenedV3<Calc.Subed<A, '1000'>, GenedV2<'1000', R>>
    : GenedV2<A, R>
  )

相信很容易就能看出规律了。那么作为一个充满智慧，深谙递归之道的程序员，你会就这么不停复制粘贴下去吗？

TS 类型编程中的循环由递归实现。为了解决复制粘贴，我们可以实现一个递归，从这个类型的规律入手。

看这个类型，首先我们想到，可以把 '10'，'100'，'1000' 这类字面量都抽成参数。于是首先我们要实现一个类型，可以根据一个字符串形式的数字 $N$ 生成字符串形式的 $10^N$

type Power<
  N extends string,
  R extends string = '1'>
  = (Calc.IsNotless<N, '1'> extends true
    ? Power<Calc.Subed<N, '1'>, `${R}0`>
    : R
  )

type A = Power<'2'> // "100"
type B = Power<'5'> // "100000"

之后我们便可抽字面量。

type GenedV0<
  A extends string,
  R extends string = ''>
  = (Calc.IsNotless<A, Power<'0'>> extends true
    ? GenedV0<
      Calc.Subed<A, Power<'0'>>,
      `${R}Z`
    >
    : R
  )

type GenedV1<
  A extends string,
  R extends string = ''>
  = (Calc.IsNotless<A, Power<'1'>> extends true
    ? GenedV1<
      Calc.Subed<A, Power<'1'>>,
      GenedV0<Power<'1'>, R>
    >
    : GenedV0<A, R>
  )

// 后略……

然后我们发现，第二个需要入手的地方就是每个类型的名字。我们可以使用一个新的类型参数代替名字里的数字。

照葫芦画瓢，我们随便找一个类型（比如 GenedV3 或者 GenedV2）复制一遍，再把它的数字都改成类型参数就可以了。

如果你在跟着这篇文章实践，发现不知道为什么编辑器卡住了，不要怀疑，就是递归太深导致的。建议马上重启编辑器。

type MaxV = '6'

type Gened<
  A extends string,
  R extends string = '',
  L extends string = MaxV>
  = (Calc.IsNotless<A, Power<L>> extends true
    ? Gened<
      Calc.Subed<A, Power<L>>,
      Gened<Power<L>, R, Calc.Subed<L, '1'>>,
      L
    >
    : Gened<A, R, Calc.Subed<L, '1'>>
  )

如果你放置三分钟后依然没有报错，那么说明你成功了。

接下来就差最后一步了，我们只需要参考 GenedV0，补上递归边界：

type MaxV = '6'

type Gened<
  A extends string,
  R extends string = '',
  L extends string = MaxV>
  = (Calc.IsNotless<A, Power<L>> extends true
    ? Gened<
      Calc.Subed<A, Power<L>>,
      (L extends '0'
        ? `${R}Z`
        : Gened<Power<L>, R, Calc.Subed<L, '1'>>
      ),
      L
    >
    : (L extends '0'
        ? R
        : Gened<A, R, Calc.Subed<L, '1'>>
      )
  )

待确认无误——也就是所有字面量都变成了类型参数，所有边界条件都考虑清楚，且放置三分钟后仍不报错——后，欢呼吧！终于是伟大的成功，你完成了递归的终极形态！

解决诡异的情况

如同所见的那样，泛型 Gened 的最后一个参数 L 是用来替代改造前那堆类型的名字后面的 V* 的。根据上面过河的比喻，我们知道 L 其实就表示我们拽了最多 L 个人用来过河，所以 L 参数越大，能生成的字符串的最大长度就越大。

我们对上面的类型 Gened 测试一下：

`L`	最大生成长度
`'0'`	$999$
`'1'`	$9980$
`'2'`	$99700$
`'3'`	$116810$
`'4'`	$117880$
`'5'`	$117850$

欸，是不是哪里不对劲？

为何 L 为 '0' 、 '1' 、 '2' 的时候生成的字符串的最大长度有规律可循，到 '3' 、 '4' 、 '5' 的时候却变得奇怪起来，甚至 '5' 相较于 '4' 反而还减少了。

这里可能是 TS 的优化导致的。我们修改一下就可以解决这个问题：

  type MaxV = '3'
+ type Add<A extends string, B extends string> = `${A}${B}`

  type Gened<
    A extends string,
    R extends string = '',
    L extends string = MaxV>
    = (Calc.IsNotless<A, Power<L>> extends true
      ? Gened<
        Calc.Subed<A, Power<L>>,
-       (L extends '0'
-         ? `${R}Z`
-         : Gened<Power<L>, R, Calc.Subed<L, '1'>>
-       ),
+       Add<R, L extends '0'
+         ? `Z`
+         : Gened<Power<L>, '', Calc.Subed<L, '1'>>
+       >,
        L
      >
      : (L extends '0'
        ? R
        : Gened<A, R, Calc.Subed<L, '1'>>
      )
    )

type MaxV = '3'
type Add<A extends string, B extends string> = `${A}${B}`

type Gened<
  A extends string,
  R extends string = '',
  L extends string = MaxV>
  = (Calc.IsNotless<A, Power<L>> extends true
    ? Gened<
      Calc.Subed<A, Power<L>>,
      Add<R, L extends '0'
        ? `Z`
        : Gened<Power<L>, '', Calc.Subed<L, '1'>>
      >,
      L
    >
    : (L extends '0'
      ? R
      : Gened<A, R, Calc.Subed<L, '1'>>
    )
  )

可以看出，在修改前的版本，当我们需要通过下一层递归来帮我们“踩那些没有踩到的石头”时，我们把之前的结果字符串 R 传入下一次递归，以此来拼接 R 与下一次递归得到的字符串。而这里修改后的版本给下一次递归传入的是一个空字符串 ''，并通过一个 Add 类型来拼接 R 与下一次递归得到的字符串。

那么为什么这样子就能使得递归最大次数变多呢？

据本人推测，在修改前的版本，我们传入 R 时，这个 R 的具体类型应该还不会被计算出来，还是保留着一坨不知道什么东西。被放进下一次递归中后，又会再被堆上一大坨不知道什么东西——依然不会被计算出来。最终堆的太多，爆了。

而如果使用 Add，就会在将 R 变成 `${R}` 的过程中，把 R 的准确类型得到了。

按照这么个理论，也可以省略 Add 这个泛型，直接把 Add 的两个参数装进模板字符串。实际测试中确实可以这么做。然而不知道为什么，虽然在编译时 tsc 不会报错，但 VSCode 中的语言感知服务——就是基于 tsc 的那个让你鼠标放到代码上就有类型提示的东西——却会不停崩溃。（原来 VSCode 的语言服务立即崩溃超过 $5$ 次就不会再重启了）

修改后的测试结果：

`L`	最大生成长度
`'0'`	$999$
`'1'`	$9980$
`'2'`	$99700$
`'3'`	$996000$
`'4'`	$9950000$
`'5'`	$99400000$

可以看出这次就完全符合预计了。

步子迈大点

虽然现在才提这件事，但是根据 Power 泛型，我们的 L 其实是表示的 $10^{1 \times L}$ 次递归，套用我们上面过河的比喻，就是说我们拽来的人最多只给我们踩 $10^1$ 个石头。

而我们讲过尾递归的限制是 $1000$，也就是 $10^3$。

相信这意味着什么就不用我多说了，哈哈。我们可以来把 Power 改造一下。

不过考虑到把 $1000$ 次全用完可能会出些问题，我们这里只用 $900$ 次。

type Power<
  A extends string,
  R0 extends string = '1',
  R1 extends string = ''>
  = (Calc.IsNotless<A, '1'> extends true
    ? Power<
      Calc.Subed<A, '1'>,
      Calc.Subed<`${R0}0`, R0>,
      `${R1}00`
    >
    : `${R0}${R1}`
  )

type A = Power<'2'> // "810000"
type B = Power<'5'> // "590490000000000"

于是我根据之前测试的结果得到了一个公式 $M=(999-L)P^L$。其中 $M$ 表示最大迭代次数，$L$ 表示 L 所代表的数，$P$ 表示“拽来的人”给我们“踩”的“石头”数量。

测了 L 为 '0' 、 '1' 、 '2' 的情况，与公式的结果完全匹配：

`L`	最大生成长度
`'0'`	$(999-0) \cdot 900^0=999$
`'1'`	$(999-1) \cdot 900^1=898200$
`'2'`	$(999-2) \cdot 900^2=807570000$

测试中 VSCode 的语言感知服务在字符串长度大于五亿的时候计算类型就很吃力了。当 L 为 '3' 的时候，根据公式，理论上能生成的最长的字符串应该是 $726084000000$ 个字符。实际上真输入这个数让他生成，得到的也只是 any 类型了。

回过头来和本文一开始的 $49$ 次递归相比，有没有感觉这个结果十分吓人呢！

本篇完

posted on 2023-01-27 04:50 肉丁土豆表阅读(1439) 评论(0) 编辑收藏举报

刷新页面返回顶部

`L`	最大生成长度
`'0'`	\(999\)
`'1'`	\(9980\)
`'2'`	\(99700\)
`'3'`	\(116810\)
`'4'`	\(117880\)
`'5'`	\(117850\)

`L`	最大生成长度
`'0'`	\((999-0) \cdot 900^0=999\)
`'1'`	\((999-1) \cdot 900^1=898200\)
`'2'`	\((999-2) \cdot 900^2=807570000\)

肉丁土豆园地

公告

TS 类型编程 终极优化：递归、尾递归、递归的递归