15-445课程学习及项目记录
课程地址
https://15445.courses.cs.cmu.edu/fall2022/
官方项目地址
https://github.com/cmu-db/bustub
学习视频
Moody-老师
我不是匠人
参考
BusTub 养成记:从课程项目到 SQL 数据库
CMU15-445 22Fall通关记录
CMU 15445 -2022通关记录
公开课笔记
从0到1数据库内核实战教程
原理内容总结
数据库管理系统按工作任务分类
OLTP(On-Line Transaction Processing):传统数据库的类型,需要大量读写。适合按行存储。
OLAP(On-Line Analytical Processing):执行复杂查询,对大量数据聚合。适合按列存储。
OLTP + OLAP
物理存储机制
为什么不直接使用操作系统已有的内存管理机制?因为如果这样,操作系统只将数据库的请求看做普通的输入输出,并不能理解数据库系统真正的目的,在缓存的替换,进程线程的调度等方面影响效率。
数据库保存位置:大部分数据库存在硬盘中,一些存在内存中(redis)。
数据库保存的形式:1个或多个文件
数据库管理系统将文件分为多个页page来管理,每个页有自己的pageid,并且能够映射到真实的物理地址。
如何组织这些页:有两种方式。一个是通过链式的方式,一条链连接空页,一条链连接有数据的页。一个是通过页目录的形式。
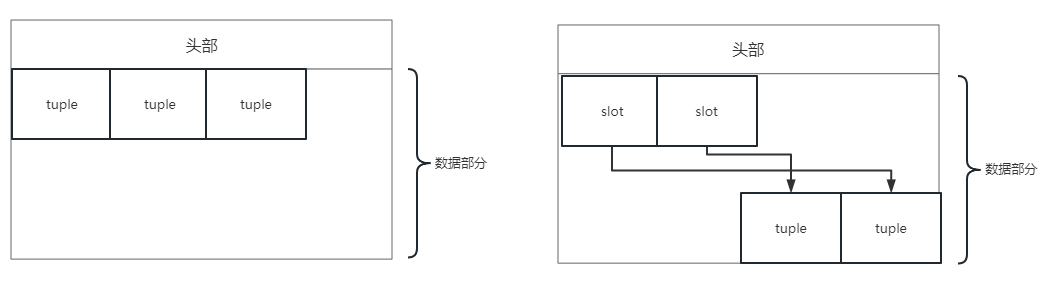
每个页的空间布局
每个页分为头部和数据部分。
头部保存元数据:页大小,校验和,压缩算法等
数据部分保存数据tuple(也可以是对数据的操作,主要应用于KV数据库)。数据在页中可以按顺序存放,也可以按槽slot存放,槽指向每条数据的位置。
通过槽页式的方式,可以只用一个数组(slot)就可以以小开销存储变长记录
插入删除时只用维护slot就可
每条数据的布局
每条数据也有一个头,之后真正要保存的数据字段按顺序紧挨存放。
一些字段可能为空:头中需要存储哪个字段为空
一些字段可能较大:指向一个额外的页来保存
数据字段可能有精度问题:采用字符串格式保存

行存储与列存储
行存储:
利用空间局部性,减少访问一条数据的开销
列存储:
便于聚合分析
相同类型的值存在一起,便于压缩
与宽列式存储区分(bigtable中)
如
alice:{
age: 10
grade:{
math:90
chinese:90
}
}
bob:{
age: 11
grade:{
math:91
chinese:92
}
}
age是一个列族,grade是一个列族,相同的列族存在一起,但列族中的数据按行存
列族grade
列键 subject value
alice math 90
alice chinese 90
bob math 91
bob chinese 92
缓存
将经常使用的页保留在缓存池中,要控制读入数据到缓存池的时间和将更新数据从缓存池写回硬盘的时间
缓存池通过页表记录缓存池中有哪些页,记录哪些页被修改过,哪些先不要被替换
为什么用缓存池,而不用mmap
https://fanjingbo.com/post/mmap-is-shit-in-dbms/
缓存池优化策略
- 每个数据库一个缓存池
- 每种类型的页一个缓存池
- 页预读取,读一个页预测下一个要读的页
- scansharing,如果两个查询正好做相同查询,则将两个查询合二为一
- 缓存池bypass,对于一些不需要缓存的数据不要将其放入缓存池
缓存替换策略:
- LRU最近最少使用
- CLOCK 像钟表一样选择,如果读过标记为1,没读过要将1设为0,如果本来是0就替换
- LRU-K
缓存池中页的查找——哈希表
哈希表由哈希函数和哈希结构组成
哈希函数:CRC-64,murmurhash等
哈希结构:
- 静态哈希结构
- 开放地址哈希:碰撞时放入下一个位置,删除时,使用墓碑标记或将之后的向前移动
- 罗宾汉哈希:插入时记录碰撞次数,碰撞时,碰撞次数少的往后移,多的占位置
- 布谷鸟哈希:使用多个哈希函数和哈希表
- 动态哈希结构
- 链式哈希:每个key指向一个链式数据结构,可以放多个碰撞的值
- 可扩展哈希:根据全局标志位指明的位数将其分入不同哈希表中,如果哈希表满了,则全局标志位数加1,并将哈希表分割,重新建立对应关系。
- 线性哈希:设置一个溢出指针,每当有溢出时,先连接一个新的空间保存,然后将分离指针指向的位置分家,分离指针指向下一个位置。分离指针之上的用新的哈希,之下的用旧的哈希
索引
本质为部分属性预先抽取出来并排好序的小表
实现索引的数据结构:b+树等
在b+树中保存的主要为KV值,K为列的属性值,V为一条记录的地址(页号加slot)或者就是真正要查找的数据
b+树的设计优化:
b+树节点最好是页大小页的整数倍
节点删除插入时会有合并的动作,很影响效率,需要设置合适的合并阈值
节点内数据的查找可以使用多种方法,如二分查找等
可以对K进行前缀压缩,合并共同前缀的K,只存不一样的,减少空间
可以批量插入,将插入数据排好序后再建b+树
索引类别
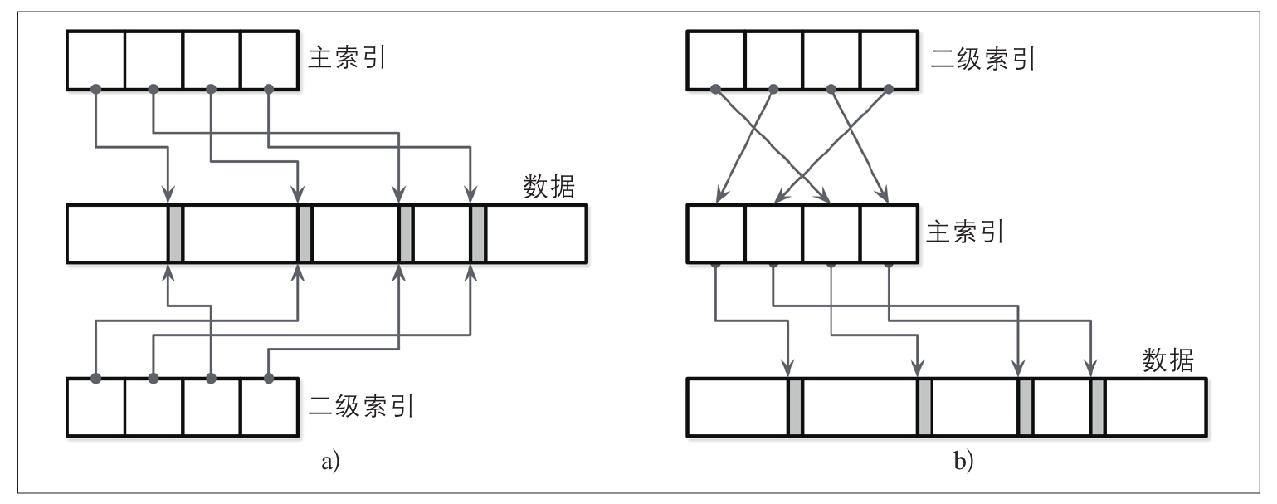
一级索引:主键上的索引,其它的都为二级索引
聚簇索引:数据直接保存在索引中,且按顺序保存(主键索引通常是聚簇的,二级索引不一定)
非聚簇索引:只保存数据偏移量
索引可以直接通过偏移量指向数据,也可以通过主键索引再指向数据,如下图a和b
一种可以减少读取数据的成本,一种可以减少索引更新的成本(mysql innodb中二级索引就需要再查询主键索引,称为回表)
索引并发
锁的实现方案:
互斥锁:操作系统支持的锁,竞争的线程会阻塞。但不能应对大规模并发场景(线程唤醒开销大)
自旋锁:获取不到锁会循环等待,消耗资源,不能应对大规模并发场景
std::atomic_flag latch;
while(latch.test_and_set)
{
// do
}
读写锁:读共享,写独占
B+树加锁方案
crabbing latch:先锁父,再锁孩子,如果不会使父分裂或合并就安全,可以释放父
乐观锁:先加读锁向下搜索,如果发现要分裂合并再重新crabbing加锁
叶子扫描时要避免死锁,发现无法获取锁要立即终止
算子
一条SQL执行要经过如下步骤
parser:进行语法解析和词法解析,生成抽象语法树
optimizer:进行逻辑和物理优化,生成执行计划
executor:执行计划
算子的种类有如下等
- 排序sort
当执行order by, group by时需要排序。但数据很多,内存放不下,不能使用普通的排序方法
方法:外部归并排序
- 聚合aggregation
当需要统计最大值,最小值,和等时需要聚合。
- 联表join
当需要合并多个表的数据重建完整的关系时使用,如where t1.id = t2.id
join输出:可以是表合并后的完整数据,也可以是连接数据的行的id,之后再根据id去查找对应的数据。join算法:
嵌套join nested loop join
for tuple r∈R
for tuple s∈S
if s与r 匹配就join
优化:
每一读入部分数据,按页将R与S中数据join(如果小表可以全部读入内存更好)
尽量在第二个循环中使用小表去匹配
如果有索引,只需查询索引
join算法比较
适合小表与小表join
index nested-loop join
遍历驱动表,根据驱动表的值通过被驱动表的索引查询匹配
如何选择驱动表:驱动表选择小表
因为设两个表行数为M N,如果M是驱动表时间复杂度为MlogN,所以驱动表M的值大小最影响时间复杂度,它应该最小
simple nested-loop join
驱动表和被驱动表上都没有索引,遍历驱动表,再遍历被驱动表去匹配
block nested-loop join
驱动表和被驱动表上都没有索引,将驱动表一部分数据读入内存,遍历被驱动表匹配,之后再读入下一批被驱动表数据,重复进行
判断在内存上提高性能,并且减少被驱动表的遍历次数(扫描的行数相比于simple减少了,内存越大,遍历次数越少,小表做驱动表扫描行数也会更小)
适合小表和大表join
hash join
将小表为驱动表(使得全部放到内存),建立哈希表,让被驱动表在哈希表中匹配
时间复杂度为M+N
不能放到内存可以使用shuffle hash join
将两个表按照join key进行分组
适合大表和大表join
优化:
使用布隆过滤器,加速匹配不上的过程,即查哈希表前先查布隆过滤器
针对hash表可能放不下:对两个表都做哈希,相同的桶保存到相同的分区,之后对相同的分区进行join
merge join
将两个表排序后,进行匹配
如果两个表本来有序时间复杂度为M+N,如果无序为MlogM+NlogN
- 投影projection
根据查询字段选择相关的列
- 过滤filter
根据where条件中的筛选条件,筛选出符合的记录
查询执行
执行模型:
- 火山模型iterator model,上层算子不断从下层拉取一条数据,直至没有数据,或者下层算子不断向上层算子推送一条数据
- 实体化模型materialization model,每一个算子计算完所有数据,再将结果交给下一个算子。适用于OLAP
- 向量化模型vectorized model,上两个模型的结合,每次计算批量的数据。适用于OLTP
如何从数据库中获取数据:
- 顺序扫描sequential scan
优化:
预读取
并行读取
Buffer Pool Bypass不经过缓存池,防止缓存被频繁替换
zone maps给每个页增加统计信息(最大,最小,平均值等),查询前先通过平均值判断是否有所需数据。但是这也占用了存储空间,当值修改时造成大量信息修改
晚物化Late Materialization算子只需要所需的列的值,如果该列的值在之后的算子不需要,只需要传递运算过后的数据的位置
heap clustering当访问的属性上有聚簇索引时,可以跳跃访问数据
- 索引扫描index scan
什么时候选择什么索引是关键,越早过滤掉越多的数据越好
- multi-index scan
使用多个索引取他们的并集或交集(可以使用位图,哈希表,布隆过滤器来取并或交)
并发查询
处理并发请求的处理模型:
- 每一个用户一个进程,依赖于操作系统进程调度,通过共享内存实现进程通信
- 使用进程池
- 使用线程,对于每个用户请求由DBMS决定拆分为几个线程,并决定线程如何调度
并发执行
- inter-query多条不同查询间的并发
- intra-query查询内的并发
针对intra-query的方法:
水平切分:把数据切分,每个线程处理一部分数据
垂直切分:每个线程负责一个算子
水平+垂直
并发I/O
- 将数据切分到不同磁盘
切分时针对数据库不同数据库放到不同磁盘,针对表,可以垂直分表保存,还可以水平分表保存(按范围分,按hash分) - 通过硬件支持十数据存放不同盘,如RAID技术
查询优化
- 基于规则的逻辑查询优化方法
将连接的谓词分开
谓词尽量下推
笛卡尔积和谓词合为一个等价的join连接
投影尽量下推,提前过滤无用数据
对于嵌套的子查询重写,或者解耦,先执行子查询
对谓调表达式重写 - 基于代价的逻辑查询优化方法
对多个查询计划的代价进行估计比较
代价种类:
物理代价:I/O开销,命中率,内存等(物理代价极其依赖于硬件)
逻辑代价:对每个算子估算代价(与算子具体算法独立)
算法代价:估计算子算法复杂度
代价模型:
postgre代价模型:代价为CPU与I/O代价按比例相加
db2代价模型
事务
事务是实现并发控制和恢复的基础。
事务是对数据的一些列操作。事务是数据库操作的最小单位,只有未执行和执行完成两个状态。
事务需要满足的标准特性——ACID
A原子性:事务中的操作要么都执行,要么都不执行。
实现方法:
日志:每执行一个SQL,记录回滚时要怎么做,要保存在内存和硬盘中
备份:对事物改的页做备份
C一致性:数据库从一个正确状态到另一个正确状态。其它三个特性就是为了实现这个目标
I隔离性:不同事务执行应该互相隔离,互不影响
实现方法:事务并发控制(悲观,乐观)
D持久性:事务对数据的修改被永久保存
实现方法:日志,备份
并发控制
并发控制支持多个用户同时读写数据
仅仅通过在获取数据时加锁是无法保证数据库的一致性的,需要其他方法
- 二阶段锁two-pase locking(悲观)
一个事务有两个阶段,在阶段1 growing阶段只能加锁,在阶段2 shrinking阶段只能解锁
问题:
级联终止(事务1修改数据后,解锁,事务2读取这些数据,事务1又回滚,事务2出现脏读,导致事务2也要回滚):可以使用严格二阶段锁,只有commit后才解锁
死锁:
死锁检测(维护一个依赖图,当发现死锁后,让环中的一个事务回滚,挑选的事务尽量选择执行时间语句少的,回滚次数少的)
死锁预防有两种思路:当年轻的事务看到锁已被老的事务占有,马上要死锁,自己结束。当老的事务看到锁被年轻的事务占有,抢锁
- Basic Timestamp Ordering (T/O)协议(乐观)
使用时间戳保证在事务提交后的状态相当于早的事务完全在晚的事务前发生的状态
时间戳采用:系统时钟或逻辑计数值或结合这两种
对每个对象X标记其最后被读写的事务的时间戳:
W-TS(X)对X标记的写时间戳
R-TS(X)对X标记的读时间戳
每次操作时,将本事务的时间戳与标记的时间戳比较,不能操作未来的数据,(事务读的时候自身时间戳不能小于X上标记的写时间,写的时候不能小于X上标记的写时间和读时间)否则自杀,重新获取新时间戳,然后数据会复制到事务本地一份,保证事务结束前得到相同数据
优化:托马斯写规则
如果事务的时间戳小于对象X上写的时间戳可以忽略事务的写,继续执行。提高并发,防止不必要的终止(思想是过去的写不用管,因为已经被未来的写覆盖了)
缺点:
长事务可能饥饿
每次都要拷贝
可能造成一些事务不能恢复,如以下情况,T2虽然已经提交,但它依赖的数据已经回滚了,当发生故障时,出现不可恢复的数据
T1 T2
W(A)
R(A)
W(A)
commit
abort
- Optimistic Concurrency Control(OCC)(乐观)
任何读的数据也要复制到本地,但是写的时候先记下来不写回,当提交时和别的事务冲突检查,没有冲突再提交,否则重来,主要有三个步骤
读阶段:将事务需要读写的集合复制到本地
校验阶段:这时得到时间戳,检查冲突(前校验或后校验)
写阶段:将本地的数据合并
只有满足下列情况之一才算通过校验
Ti在Tj前完成了所有步骤
Ti在Tj开始校验前完成。Ti没有写任何个Tj读的对象
Ti在Tj完成读前完成了读,Ti没有写任何Tj读或写的对象
缺点:
复制到本地有开销
校验和写阶段可能有瓶颈
语句全执行完才能发现冲突,产生浪费
2PC的性能瓶颈在于锁管理,OCC的性能瓶颈在于复制合并数据及校验阶段
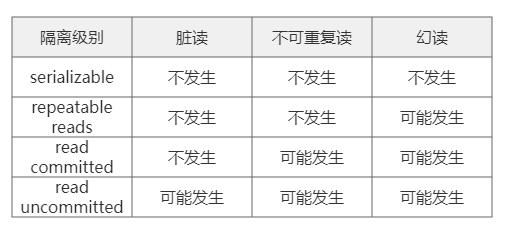
隔离级别
上述并发控制只讨论读和写,但当插入新数据或删除数据时,因为只能锁现存的,所以存在幻读问题。解决方案:
re-execute scan在提交之前再进行扫描确认
predicate locking谓词锁,给select的谓词加共享锁,给update insert,delete的谓词加独占锁
index locking索引锁,锁包含谓词的索引的页如果没有索引,对所有有关谓词的页加锁
上述并发控制都旨在将事务可序列化,但这种隔离级别有时并不需要,只需要一个更弱的隔离级别,以下为各隔离级别及可能出现的问题
MVCC多版本并发控制
在DBMS中记录数据的历史版本,优势是写不阻塞读,读不阻塞写
MVCC主要由四个部分组成:
- 并发控制协议:T/0,OCC,2PL
- 新老所本存储:
追加:新版本只是在同一表中追加一行,旧版本通过指针指向新版本
Time-travel:新建一个表存历史的版本
存增量:新建一个表存历史的版本,只存属性的变化 - 垃圾回收
移除所有事务都不需要的版本
以行记录为单位的垃圾回收:直接检查元组找老所本,找到后可以后台清理,也可以合作清理(在事务执行时顺便清理)
以事务为单位的垃圾回收:每个事务记录自己创建的老所本,当需要回收时,将自己创建的历史版本删除 - 索引管理
主键索引直接指向版本链的头部。
辅助索引要么指向主键,要么指向版本链的头部
恢复
恢复支持数据库在故障宕机时恢复到之前的状态,故障级别有:
事务级别:逻辑错误(如数据一致性问题),内部状态错误(如死锁)
系统级别:软件(如DBMS出现bug),硬件(如断电)
存储媒介级别:如无法修复的硬盘毁坏
为实现恢复,在事务执行时的方法
刷脏方式:no-steal和steal(刷脏时顺便将其它事务未提交的也提交)
提交方式:no-force和force(用户一commit就强制刷脏)
shadow paging机制:采用no-steal + force
修改时,另外复制一份数据,对它进行读写,commit时,将这些复制的页写回,最后将缓存和磁盘中旧的页删除
缺点:多余的复制开销大,commit时的操作太多
WAL write-ahead log预写日志:采用steal + no-force
在磁盘上单开一个日志文件,保存事务对数据库的修改
每次修改,生成日志保存在内存,修改数据也先在内存,commit时要将日志写到磁盘中,这样就认为成功
日志类型:
- 物理日志:记录每个二进制数据具体偏移的具体变化
- 逻辑日志:记录增删改查的操作
对比:
物理日志修改数据很多导致日志很大,逻辑日志较精简
逻辑日志较难确定语句修改了什么数据,可能有bug,且恢复时间慢
优化:混合记(使用物理逻辑日志,如只记录几号页的几号槽的数据变化)
检查点checkpoint
一段时间需要将所有日志记录和改动的数据都持久化到磁盘中,然后在日志中记录为checkpoint,这表示之前所有的数据都已经持久化,即之后恢复时前面的操作已经不需要关心。在恢复时,只需要undo检查点后没有commit事务,redo检查点后commit的事务
WAL与shadow paging相比,运行时效率更高,恢复时效率更低
为实现恢复,在故障后的恢复机制
数据库恢复原型算法——aries算法
主要思想是:预写日志WAL,回放历史数据redo,回滚数据undo
日志中每条记录都包含一个全局的日志序列号LSN log sequence numbers
flushedLSN:内存中记录上一次刷到磁盘中的log编号
pageLSN:记录内存中对页的更新的最新编号
recLSN:记录内存中对页的更新的最老编号
lastLSN:记录事务的最后日志的编号
master record:checkpoint点处的日志编号
写数据时要保证 pageLSN≤flushedLSN
事务commit流程
先记录commit log,再将 log写到磁盘,等之后将数据写到磁盘(如 checkpoint)时,写一个txn-end的log
事务abort流程
为了从WAL中找出所有与该事务相关的日志,日志中每条记录都记有prevLSN,表示事务上一条LSN是什么
回滚操作时还要额外记录类型为CLR的反向的日志,其中通过叫undonext的字段记录下一条要被undo的日志
checkpoint优化:
- checkpoint时让DBMS停止
通过加锁阻止写,不等正在运行的事务完成就checkpoint。
需要记录中间状态ATT(记录当前活动事务的表)和DPT(记录当前脏页的表) - checkpoint时DBMS依然运行
不让事务停止,也不全部刷脏(有些可能正在使用),checkpoint变为一个时间段
恢复时aries算法流程
- 分析阶段:
从最后一次成功的checkpoint往现在扫描,如果发现txn-end记录,在ATT中将对应事务删除。对于其它事务,在ATT中添加,状态记为end。如果找到事务的commit纪录,就把状态记为commit。最后得到ATT与DPT - redo阶段:
从DPT中的最小的recLSN处重做,如果日志修改的页不在DPT中,不用重做
如果页在DPT中,但对应记录的LSN小于页的recLSN(说明该日志对页的影响已经写入) - undo阶段:
处理ATT中undo状态的事务
分布式数据库
并行数据库距离近,通过高速LAN连接,分布式数据库通过公网连接
分布式数据库架构
shared everything:所有DBMS在同一cpu,同一内存,同一硬盘上(极端情况,测试时出现)
shared memory:有多个cpu,cpu机器间通过网络连接
shared disk:有多个cpu和内存,数据集中放在一个disk(存算分离)
shared nothing:各机器通过网络通信
分布式场景下的查询执行
执行模型
push:数据在哪就将sql放哪执行
pull:sql在哪就把数据拉来执行
查询计划分片:
把物理算子进行切分:先生成一个查询计划,再将它按数据分成多个部分,分发给不同的节点。
把sql进行切分:将原始的 SQL 语句按分片信息重写成多条 SQL 语句,每个节点自己在本地作查询优化。
分布式join算法
考虑SELECT * FROM R JOIN S ON R.id = S.id
情况1
节点1有S所有数据,R部分数据,节点2有S所有数据,R另一部分数据,则分别join后合并为所需数据
情况2
节点1有S部分数据,R部分数据,节点2有S另一部分数据,R另一部分数据,则分别join后合并为所需数据
情况3
节点1有S部分数据,R部分数据(但不是按join key分布的),节点2有S另一部分数据,R另一部分数据,则在R数据量很少的情况下可以将两个节点的R数据汇总起来再分别执行join,最后将结果合并
情况4数据
节点1有S部分数据,R部分数据,节点2有S另一部分数据,R另一部分数据,但都不是按join key分布的,需要将数据重分区
云系统
managed DBMS云数据库:数据库在虚拟机中,数据库是单机数据库改造而来
cloud-native DBMS云原生数据库:专为云原生环境设计
Serverless database:将计算资源与存储资源分开,当不使用时计算资源不运行,节省用户租金
项目完成记录
只完成了必做内容,在线测试排名也很差,只能说勉强完成。做的时候感觉挺难得,做完了一回顾发现又没那么难
环境:在windows上使用官方提供的docker容器,代码在windows的clion上写,在docker中运行
project 0
实现一个并发字典树来存储键值对。本项目和整个项目没有关系,只是为了入门练手
- 插入:其中注意以下情况,如下图所示
- 开始保存的键值对为(aa,2),灰色的为TrieNodeWithValue类节点
- 当插入键值对(a,1)时,要将原本普通的TrieNode类节点转为TrieNodeWithValue类节点
- 当插入键值对(abc,3)时,原本没有的键要添加进去
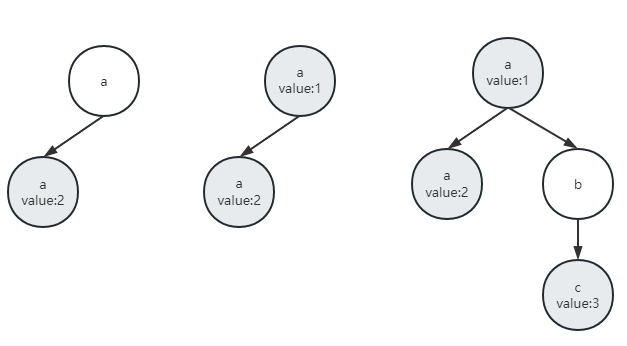
- 删除:主要有以下情况,如上图最后一个所示
- 如果要删除键值为ac的,遍历a发现有,遍历c发现没有,删除失败
- 如果要删除键值为a的,遍历可以找到,但该节点还有子节点,则把它设为不带value的节点类型(项目中直接把is_end_设为false)
- 如果要删除键值为abc,遍历可以找到,不仅要删除节点c,还要删除节点b
- 查找:查找就没什么了
- 最后加锁,我直接一把大锁
project 1
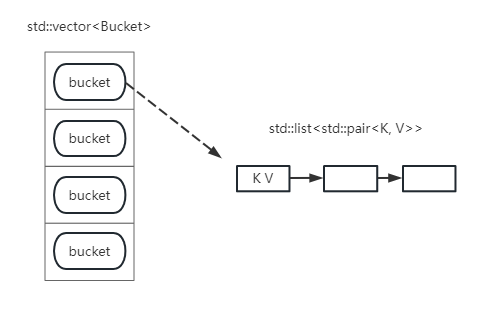
扩展哈希表
扩展哈希表本质如下所示,就是保存在一起的bucket桶,桶就是一个链表list,这里再链表中保存的是键值对
哈希是指:在插入键值对时,通过对键哈希来定位要插到哪一个桶,最后插入到桶,即链表中
扩展是指:随着插入数据的增多或减少(本项目中规定只增加),桶的数量会增多和减少
怎么实现插入扩展,这也是这一节的重点
首先给哈希表设定一个全局深度,给每个桶设定一个局部深度,一个当插入数据时,发现桶已经满了,如果此时全局深度等于局部深度则扩展,并增加相应的全局深度和局部深度。否则只增加桶,并增加自己的局部深度。如下所示
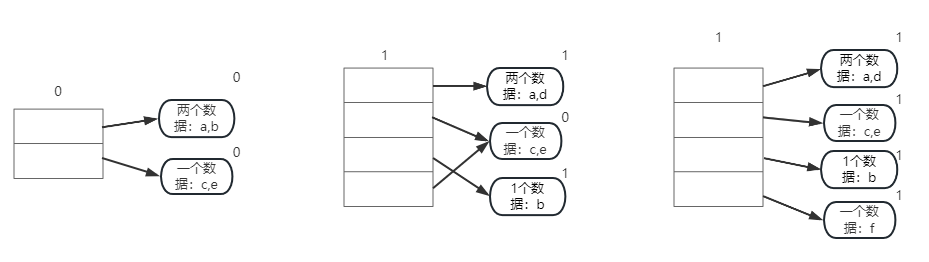
开始只有两个桶,两个桶各有两个数据ab和ce(假设这里桶最大只能存两个),全局深度和两个桶的局部深度都为0
当插入数据d时,分到第一个桶,但此时桶已满,而其局部深度又等于全局深度。所以哈希表进行扩展(这里成倍扩展),桶进行分裂(即增加一个桶,再将原来桶中的数据重新哈希分配),最后再将数据插入,并且该桶的局部深度和全局深度都要增加
当再插入数据f时,分到第二个桶,但此时桶已满,而其局部深度小于全局深度。所以哈希表不用扩展,只进行桶分裂,并且增加该桶的局部深度
其它的删除和查找操作就不赘述
关于并发控制,还是采用了一把大锁。我开始想只锁住每个桶,但这样不适用于扩展的哈希表,最后还得锁住整个哈希表。
LRU-K
LRU-K是一种缓存替换算法,是LRU的改进。LRU的策略是:替换时优先替换最久没有使用(命中的),如下所示
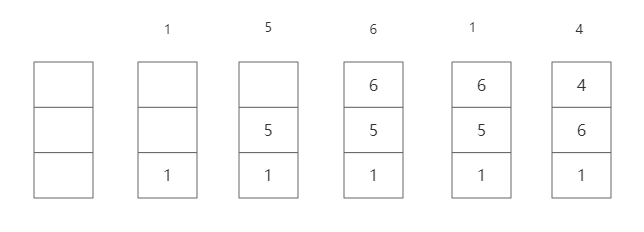
假设缓存池只能保存三个页,页表如下
先缓存1,5,6,之后查找页面1,可以在缓存中命中,最后查找页面4,缓存没有命中,读入内存后,页面4要替换掉最长时间没有命中的,即页面5
LRU-K则可以分为两个部分
开始的页面替换策略按照先进先出进行,等页面的命中次数达到K次,就按照LRU策略进行(这里是替换倒数第k次访问时间最久的)
如下所示假设k是2,开始按照先进新出替换,5命中两次达到k,就将其放入另一个队列(这个队列就用LRU进行替换),之后优先替换第一个队列的,当第一个队列不能替换时,再替换这一个队列
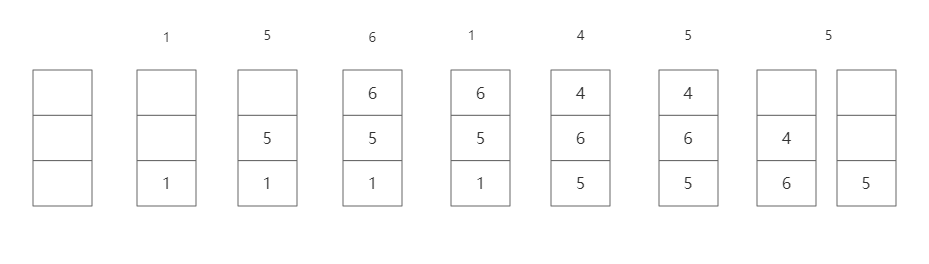
关于替换倒数第k次访问最久的拗口又不好理解,举个例子:假设k还是2,下图是达到第二次的队列,第3秒5加入队列,等到第6秒该替换谁?按照传统的LRU该替换4,因为5刚刚访问过。可LRU-K中的LRU比较的是倒数第k次(这里是倒数第二次),4倒数第2次是第四秒访问的,5倒数第二次是第三秒访问的,5最久没被访问,所以替换掉5
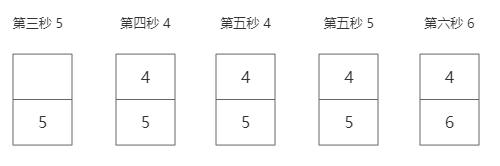
在本项目中的实现是:使用一个全局的变量,每一次获取页后,它就加1,并且每个页框(frame)有一个K大小的先进先出队列,每访问一次该页框就将当前的全局变量值加入队列。之后比较第k次访问最久时,只要比较给页框的队列头的值的大小即可
关于并发控制,还是采用了一把大锁
缓存池
结合前两个部分来对缓存进行管理
每次要读入一个页首先通过FetchPgImp函数查看缓存
根据页号查看在扩展哈希表中查看缓存池中是否有该页,如果有要更新LRU-K的相关记录,并将该页标记(pin住,防止页被替换)
缓存池中没有该页,就要看缓存池是否还有空余地方,如果有就分配一个空余页框
如果没有就要进行替换,通过LRU-K查找可以替换的页,如果该替换页发生过修改(isdirty),还需要将该页写回磁盘
最后在扩展哈希表记录页号与页框号的映射关系及其它记录,并存磁盘中将该页保存到对应的页框
关于并发控制,还是采用了一把大锁。
project 2
项目中每个B+树节点是一个页的数据,B+树的中间节点BPlusTreeInternalPage和叶节点BPlusTreeLeafPage分别继承自BPlusTreePage,中间节点和叶节点的数据结构如下所示,它的数据结构如下图。
B+树节点的数据结构由两部分组成,一个头部,一个存放键值对。头部的数据在项目注释中写的很清楚,总共占28B,保存PageType等信息。叶节点和中间节点的头部区别就是中间节点没有NextPageId (4)这一个属性,所以头部占24B
Header format (size in byte, 28 bytes in total):
---------------------------------------------------------------------
| PageType (4) | LSN (4) | CurrentSize (4) | MaxSize (4) |
---------------------------------------------------------------------
-----------------------------------------------
| ParentPageId (4) | PageId (4) | NextPageId (4)
-----------------------------------------------
而键值对采用了柔性数组保存,即从项目中MappingType array_[1]定义的array_起始array_[0]是第一个键值对,加一后array_[1]是下一个键值对
每个键值对,键是索引查找的键,值是存储数据的地址(由page_id和slot_id组成,即指向一个页和在该页中的偏移地址)
同时需要注意,项目中的树结构的如何组织的。下图中叶节点有两对KV值,中间节点也有两对KV值,但是第一对的K值可以是任意的,它不起作用。在遍历时,与第二对的K值比较,小于30就接着第一对的V值向下遍历,大于等于30就接着第二对的V值向下遍历。
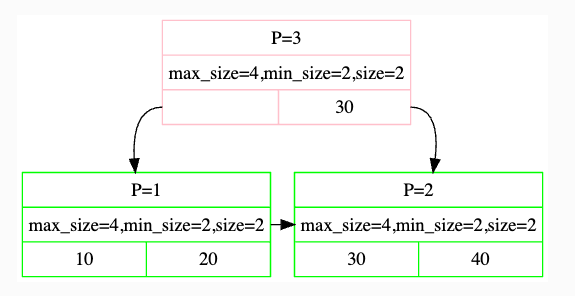
插入
- 如果B+树为空,新建节点插入,插入成功
- 不为空,如果根节点不为叶节点,先查找得到叶节点,如果本来是叶节点,不用查找也得到叶节点
2.1. 先将数据插入该叶节点
2.2. 判断节点是否需要分裂(数据量是否大于等于规定的最大值),不需要分裂则插入成功
2.3. 如果需要分裂,先分裂。先新建右节点,我采用左少右多的分法(即左节点永远保留最少的数据,如果有5个数据,左节点分2个,右节点3个)。最后维护好节点间的连接(父节点的指向,叶节点下一个节点的指向)
2.4. 再进行合并。先判断左右节点是否有父节点,如果没有父节点说明是开始时既是根节点又是叶节点,则新建根节点,并插入两对KV,第二对K为右节点第一个数据的K,V为指向右节点的页号,第一对KV的V为指向左节点的页号,K其实不起作用,但我将它写成了与第二对KV相同的K。最后维护节点节点间的联系。
2.5. 如果有父节点,则回到2.1步骤,将K值为右节点第一个数据,V为右节点页号的KV对插入,不断循环
2.6. 但是需要注意,之后的循环中处理的都是中间节点。中间节点的分裂与上述步骤中叶节点的分裂合并稍有不同。如判断中间节点是否需要分裂(数据量是否大于规定的最大值),这是由于B+树的定义规定的
删除
- 如果B+树为空,直接返回
- 不为空,则查找得到删除数据所在的叶子节点。然后删除数据,如果删除的数据在叶节点中排在第一个,且该叶节点有父节点,还要更新父节点中指向该节点的K值,将其设为新的叶节点的第一个的K值
- 如果删除后节点数据为空,如果还是根节点,就更新为空树。如果不是根节点,就要将父节点中指向该页的KV删除。
3.1. 如果父节点是根节点,删除后返回
3.2. 如果不是父节点,但删除后,节点的数据量依然大于等于最小值,则返回。否则,需要和左右兄弟合并(我这里合并的尝试是先和左借,再和右借,再和左合并,再和右合并)
3.3. 最后再看该父节点的父节点,从3.1循环 - 如果删除后节点数据满足最小限制,返回
- 如果删除后节点数据不满足最小限制,同样需要和左右兄弟合并(依然是尝试是先和左借,再和右借,载和左合并,再和右合并),并且与左兄弟或右兄弟合并后同样要查看父节点,重复3.1之后的步骤
B+树并发
这里采用的是用latch crabbing螃蟹锁的方式实现主要思想是先锁住父节点,再锁住子节点,如果子节点安全,就可以给父节点解锁,从而不断搜索得到叶节点。
“安全”指的是:当插入时,如果该节点插入后依然满足数据量最大的限制就安全(意味着不用分裂,也就不用修改父节点,父节点就可以解锁)。当删除时,如果该节点删除后依然满足数据量最小的限制就安全。
另外每次fetch页面的时候都是pin住了该页,不用后需要unpin,也可以通过Transaction中的函数AddIntoPageSet,将该页记录下来,统一unpin解锁
project 3
项目中采用的是自上而下的火山模型
在项目中通过catalog和要查找的tableid找到对应表的元信息tableinfo,在元信息中可以找到存储表数据的页的位置tableheap,通过页的位置可以遍历得到每一个页,在每一个页中可以得到每一条元组
SeqScan
最底层的算子,在Init中不需要初始化下层算子,在Next中每遍历得到一条数据就返回true,没有数据就返回false
Insert
初始化子算子,执行子算子的next得到数据要插入的RID,在RID处插入数据,然后不断循环(执行子算子,插入数据),直到没有数据插入,返回插入数据的条数(即使没有数据插入,也要返回插入0条数据)。同时要维护好表的索引
Delete
和Insert相似,其中删除时只是将数据标记为删除
IndexScan
与SeqScan,只不过是通过project 2实现的B+树查询得到数据所在的RID,再通过RID去表中查找得到数据
Aggregation
在init中就需要初始化子算子,并得到所有数据。数据都被插入一个哈希表中,表中key值就是ordby字段,value就是查询想要得到的各个统计数据。
举个例子,对下表执行如下SQL
slect min(math), max(chinese) from table order by math;
id math chinese
1 80 70
2 80 66
3 90 70
4 95 80
- 首先得到一条数据 1 80 70,通过MakeAggregateKey和MakeAggregateValue得到key与value的数据为[80] [80 70]
- 然后通过InsertCombine函数插入到哈希表中
- 然后通过CombineAggregateValues对数据聚类,CombineAggregateValues函数中定义了5种聚类处理过程count(*),count(), min(),max(),sum(),这里执行min,就需要将80与原来保存的key为80对应的value比较(本例中现在是第一条数据,所以和一个初始值比较),用最小值更新这个value
- 最后哈希表就保存了[80] [80 70]这一对数据
- 在得到数据2 80 66,哈希表就变成了[80][80 66]
- count(*)只要有一条数据,统计数量就加一,count()只有统计的该字段不为空,数量才加一
- 将数据准备完成后,最后才在next函数中将数据一条条返回
NestedLoopJoin
join有:
- inner join:只有两表连接字段相等才显示
- left join:以左表为基础,右表只显示与连接字段匹配的记录,与左表不匹配的用空填充
- right join:以右表为基础
项目中实现inner join 和left join
在init中对左右子算子初始化,并且执行右子算子,得到右表的所有数据
在next中,首先判断是否上次已经开始join(两个表都遍历到中间),如果是要从上次左表的记录和上次右表的记录的下一个开始匹配。
主要针对下面情形(假设join为table1.chinese = table2.chinese),如上一次匹配正好匹配到左表2 60 50与右表1 60 50成立。这一次将左表2 60 50与右表2 66 50匹配看是否成立
table1
id math chinese
1 80 70
2 60 50
3 76 50
table2
id english chinese
1 60 50
2 66 50
3 70 50
如果是第一次匹配或上一次已经将右表遍历完,就需要读入新的左表记录
在join中就是遍历右表看是否有与指定左表记录匹配的记录
如果有就拼在一起
如果没有并且是该左表记录第一次匹配并且是left join,就要用空值与左表记录拼在一起
最后将拼在一起的结果返回
NestedIndexJoin
与NestedLoopJoin类似,只不过匹配时,如果匹配字段上建有索引,就会通过B+树查找是否有要匹配的key
Sort
在init中读入所有记录,并对记录进行排序即可
Limit
记录已经读取的数据量,当达到限制时就不再返回数据
Top-N Optimization Rule
当有两个连续的算子为sort和limit时,执行过程为读取所有数据,然后排序,最后返回需要的n条数据
这时就可以优化将两个算子合并,在读取数据时就维护好一个数据结构,只保存最大/最小的n条记录,这里我使用堆
如果是降序,建一个大小为n的小根堆(维护一个含有n个最大数据的结构,这n个最大数据中最小的做根),每次读取数据,插入到堆中,如果数据还没有堆顶大,就不用插入(都没有最小的大,也就不用插入)。否则代替堆顶,并下沉。
如果是升序,建一个大小为n的大根堆,每次读取数据,插入到堆中,如果数据还没有堆顶小,就不用插入。否则代替堆顶,并下沉。
下沉时,以小根堆举例。如果已经沉到叶子,或者比两个子节点都小,就不用下沉。否则与最小的子节点对换,然后继续下沉。
将所有数据读取完成后,在next中从后往前输出n条数据(因为如果是降序,需要从大输出数据,但我建的是小根堆)。
Optimizer部分可以参考已有的其它Optimizer的代码。大致方法是递归遍历查询计划,看算子是否为limit且子算子是sort,这样就构建一个新topn算子代替这两个算子加入优化的查询计划
project 4
本项目就要实现一个锁管理器,每个事务的加锁解锁请求都要通过锁管理器实现。
锁管理器维护了两个哈希表,一个记录了对表的锁请求,一个记录对行的锁请求。通过表id可以得到该表的请求队列,请求队列中记录了各事务对该表的请求,请求中记录个事务想要对该表申请什么类型的锁,该请求是否被满足等属性
锁表
- 判断事务状态是否已经是committed或abort,是则抛出异常
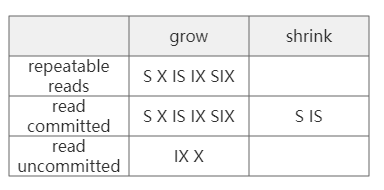
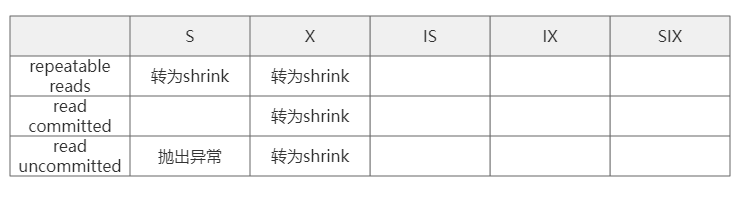
- 根据事务所处阶段和隔离级别判断请求锁的类型是否满足下表所示
- 查看该事物之前是否有该表的锁。
3.1 如果有且所类型相同,不作处理返回。
3.2 如果类型不同,但有别的事务正在锁升级,抛出异常
3.3 如果类型不同,且没有别的事物正在升级锁,判断是否可以升级,不能升级要抛出异常,如果能升级要在请求队列标注该事务正在升级,并将原锁删除
IS -> [S, X, IX, SIX]
S -> [X, SIX]
IX -> [X, SIX]
SIX -> [X]
- 将新的锁请求插入队列,开始阻塞判断是否可以得到锁
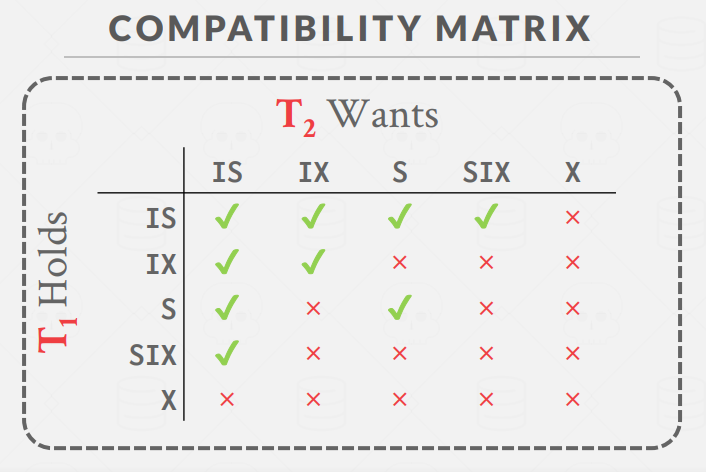
- 在阻塞中,判断事务请求的锁与请求队列中已经授予的锁是否兼容,不兼容抛出异常
锁之间兼容性如下所示
- 判断是否存在锁升级,如果要锁升级的事务与该锁请求的事物相同,立即返回停止阻塞,授予锁
- 如果要锁升级的事务与该锁请求的事物不同或者不存在锁升级,从头到尾遍历查看队列未被授予的锁与请求的锁是否兼容,不兼容要抛出异常
- 如果遍历到未被授予的锁的事物与锁请求的事物相同,立即返回停止阻塞,授予锁(这时可能前面的锁还没被授予,但是既然遍历到这说明该锁与前面的锁兼容,之后前面这些锁也会授予的,相当于同时授予锁)
解锁表
- 判断是否有该表的锁,没有就抛出异常
- 判断表中的行锁是否还没有解锁, 没有解锁就抛出异常
- 如果事务状态还是grow,就要根据隔离级别和解锁的锁类型判断是否更改事务状态为shrink
- 最后在请求队列中将该锁删除,并通知其它正在阻塞的事务
解锁行也与此类似
死锁检测
二阶段锁会产生死锁问题,所以需要死锁检测机制
大致思想就是根据请求队列绘制事物之间的依赖有向图,通过深度优先遍历算法检测图中是否有环,如果有环,得到环中最新的事物(事务id号最大),将事务状态设为abort,并重新绘制依赖图,重新检测是否有环,不断循环。
并发查询
在算子(scan insert delete)执行时要对表查询,修改,所以在初始化时要根据隔离级别通过锁管理器锁表,在具体查询时锁行,在读类型的算子(scan)中read uncommitted是不需要加锁的。在最后结束时,对于读类型的算子(scan),read committed可以将所有的锁解锁。在锁类型的算子(insert delete)中只需要加锁,当commit或abort时再全部解锁。
加锁的类型:对表选择意向锁IS IX,对行选择S X锁
由此也可知不同隔离级别可能出现不同问题,本项目只支持后三种隔离级别
- repeatable reads执行过程中只加锁,最后commit再解锁,所以不可能出现脏读,不可重复读,但是会出现幻读(比如事务1读了10行数据,事务2却加了1行数据,事务1再读就发现有11行数据)
- read committed在执行过程中即使更改事务状态到shrink,还能加S锁,所以可能发生不可重复读(比如事务1读了数据1,之后解锁,事务2修改了数据1,事务1可以再读数据1时发现两次读取的数据1不一致)
- read uncommitted在执行过程中对读不加锁,所以可能出现脏读(比如事务1修改了数据1,还没提交,但由于不加锁事务2可以读了数据1,之后事务1回滚,事务2出现脏读)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号