如果让我手写......
字符串
#include <iostream>
#include <cstring>
class MyString {
private:
char* m_data;
size_t m_length;
public:
MyString():m_data(nullptr),m_length(0){}
MyString(const char* str) {
m_length = strlen(str);
m_data = new char[m_length + 1];
strcpy(m_data, str);
}
~MyString() {
delete[]m_data;
}
MyString(const MyString& other) {
m_length = other.m_length;
m_data = new char[m_length + 1];
strcpy(m_data, other.m_data);
}
MyString& operator=(const MyString& other) {
if (this != &other) {
delete[]m_data;
m_length = other.m_length;
m_data = new char[m_length + 1];
strcpy(m_data, other.m_data);
}
return *this;
}
MyString(MyString&& other) noexcept {
m_length = other.m_length;
m_data = other.m_data;
other.m_length = 0;
other.m_data = nullptr;
}
MyString operator+(const MyString& other) const {
MyString newString;
newString.m_length = m_length + other.m_length;
newString.m_data = new char[newString.m_length + 1];
strcpy(newString.m_data, m_data);
strcat(newString.m_data, other.m_data);
return newString;
}
};
vector
#include <iostream>
#include <stdexcept>
template<typename T>
class MyVector {
private:
T* m_data;
size_t m_size;
size_t m_capacity;
public:
MyVector():m_data(nullptr),m_size(0),m_capacity(0){}
~MyVector() {
delete[]m_data;
}
T& operator[](size_t index) {
if (index >= m_size) {
throw std::out_of_range("index out of range");
}
return m_data[index];
}
void push_back(const T& value) {
if (m_size >= m_capacity) {
reserved(m_capacity == 0 ? 1 : m_capacity * 2);
}
m_data[m_size] = value;
m_size++;
}
void push_back(T&& value) {
if (m_size >= m_capacity) {
reserved(m_capacity == 0 ? 1 : m_capacity * 2);
}
m_data[m_size] = std::move(value);
m_size++;
}
void reserved(size_t size) {
if (size > m_capacity) {
T* new_data = new T[size];
for (size_t i = 0; i < m_size; ++i) {
new_data[i] = std::move(m_data[i]);
}
delete[]m_data;
m_data = new_data;
m_capacity = size;
}
}
};
智能指针
template<typename T>
class MyShared_ptr {
private:
T* m_ptr;
size_t* m_count;
public:
MyShared_ptr() :m_ptr(nullptr), m_count(nullptr) {}
explicit MyShared_ptr(T* ptr) : m_ptr(ptr), m_count(new size_t(1)) {}
MyShared_ptr(const MyShared_ptr& other) :m_ptr(other.m_ptr), m_count(other.m_count) {
if (m_count) {
(*m_count)++;
}
}
MyShared_ptr& operator=(const MyShared_ptr& other) {
if (this != &other) {
release();
m_ptr = other.m_ptr;
m_count = other.m_count;
if (m_count) {
(*m_count)++;
}
}
return *this;
}
~MyShared_ptr() {
release();
}
private:
void release() {
if (m_count) {
(*m_count)--;
if (*m_count == 0) {
delete m_ptr;
delete m_count;
m_ptr = nullptr;
m_count = nullptr;
}
}
}
};
LRU
#include <iostream>
#include <unordered_map>
#include <list>
using namespace std;
class LRU {
private:
map<int, list<pair<int, int>>::iterator> table;
list<pair<int, int>> data;
int size;
public:
int get(int key) {
if (table.find(key) == table.end()) {
return -1;
}
data.splice(data.begin(), data, table[key]);
return table[key]->second;
}
void put(int key, int value) {
if (table.find(key) == table.end()) {
table[key]->second = value;
data.splice(data.begin(), data, table[key]);
return;
}
if (table.size() == size) {
table.erase(data.back().first);
data.pop_back();
}
data.emplace_front(key, value);
table[key] = data.begin();
}
};
线程池
#include <iostream>
#include <thread>
#include <functional>
#include <queue>
#include <vector>
#include <mutex>
#include <condition_variable>
#include <future>
class ThreadPool {
private:
std::vector<std::thread> threads;
std::queue<std::function<void()>> tasks;
std::mutex queueMutex;
std::condition_variable condition;
bool stop;
public:
ThreadPool(size_t num_threads) :stop(false) {
for (size_t i = 0; i < num_threads; ++i) {
threads.emplace_back([this] {
while (true) {
std::function<void()>task;
{
std::unique_lock<std::mutex> lock(queueMutex);
condition.wait(lock, [this] {return stop || !tasks.empty(); });
if (stop && tasks.empty()) {
return;
}
task = std::move(tasks.front());
tasks.pop();
}
task();
}
});
}
}
template<class F, class... Args>
auto enqueue(F&& f, Args&&... args)-> std::future<typename std::result_of<F(Args...)>::type> {
using ReturnType = typename std::result_of<F(Args...)>::type;
auto task = std::make_shared<std::packaged_task<ReturnType()>>(std::bind(std::forward<F>(f), std::forward<Args>(args)...));
std::future<ReturnType> result = task->get_future();
{
std::unique_lock<std::mutex> lock(queueMutex);
if (stop) {
throw std::runtime_error("enqueue on stopped threadpool");
}
tasks.emplace([task]() {(*task)(); });
}
condition.notify_one();
return result;
}
~ThreadPool() {
{
std::unique_lock<std::mutex> lock(queueMutex);
stop = true;
}
condition.notify_all();
for (std::thread& thread : threads) {
thread.join();
}
}
};
int main() {
ThreadPool pool(4);
std::vector<std::future<int>> results;
for (int i = 0; i < 8; ++i) {
results.emplace_back(pool.enqueue([i] {
std::this_thread::sleep_for(std::chrono::seconds(i));
return i * i;
}));
}
for (auto&& result : results) {
std::cout << result.get() << ' ';
}
}
跳表
#include <iostream>
#include <vector>
#include <random>
// 跳表节点
struct SkipNode {
int value;
std::vector<SkipNode*> forward; // 每层的前向指针
SkipNode(int val, int level) : value(val), forward(level, nullptr) {}
};
class SkipList {
public:
SkipList() : maxLevel(1), generator(std::random_device()()) {
// 创建头节点
head = new SkipNode(INT_MIN, maxLevel);
}
~SkipList() {
SkipNode* current = head;
while (current) {
SkipNode* next = current->forward[0];
delete current;
current = next;
}
}
// 插入元素
void insert(int value) {
int level = randomLevel();
// 如果插入的元素的层数高于当前最大层数,则更新最大层数
if (level > maxLevel) {
head->forward.resize(level, nullptr);
maxLevel = level;
}
// 查找插入位置
SkipNode* current = head;
std::vector<SkipNode*> update(level, nullptr); // 记录每层应更新的节点
for (int i = maxLevel - 1; i >= 0; --i) {
while (current->forward[i] && current->forward[i]->value < value) {
current = current->forward[i];
}
update[i] = current;
}
current = current->forward[0];
// 如果元素已存在,则不插入
if (current && current->value == value) {
return;
}
// 创建新节点并插入到每层链表中
SkipNode* newNode = new SkipNode(value, level);
for (int i = 0; i < level; ++i) {
newNode->forward[i] = update[i]->forward[i];
update[i]->forward[i] = newNode;
}
}
// 删除元素
void erase(int value) {
// 查找待删除的元素位置
SkipNode* current = head;
std::vector<SkipNode*> update(maxLevel, nullptr);
for (int i = maxLevel - 1; i >= 0; --i) {
while (current->forward[i] && current->forward[i]->value < value) {
current = current->forward[i];
}
update[i] = current;
}
current = current->forward[0];
// 如果元素不存在,则不删除
if (!current || current->value != value) {
return;
}
// 更新每层链表中的指针
for (int i = 0; i < maxLevel; ++i) {
if (update[i]->forward[i] == current) {
update[i]->forward[i] = current->forward[i];
}
}
// 删除节点
delete current;
// 更新最大层数
while (maxLevel > 1 && !head->forward[maxLevel - 1]) {
--maxLevel;
}
}
// 查找元素是否存在
bool contains(int value) const {
SkipNode* current = head;
for (int i = maxLevel - 1; i >= 0; --i) {
while (current->forward[i] && current->forward[i]->value < value) {
current = current->forward[i];
}
}
current = current->forward[0];
return current && current->value == value;
}
// 打印跳表
void print() const {
for (int i = maxLevel - 1; i >= 0; --i) {
SkipNode* current = head->forward[i];
std::cout << "Level " << i << ": ";
while (current) {
std::cout << current->value << " ";
current = current->forward[i];
}
std::cout << std::endl;
}
}
private:
int maxLevel; // 当前最大层数
SkipNode* head; // 头节点
std::default_random_engine generator; // 用于生成随机层数的随机数引擎
// 生成随机层数
int randomLevel() {
static const float P = 0.5; // 层数减少的概率
int level = 1;
while (generator() < P && level < maxLevel + 1) {
++level;
}
return level;
}
};
int main() {
SkipList skipList;
skipList.insert(3);
skipList.insert(6);
skipList.insert(2);
skipList.insert(9);
skipList.insert(1);
skipList.insert(7);
skipList.print(); // 输出跳表的每层链表
std::cout << "Contains 3: " << std::boolalpha << skipList.contains(3) << std::endl;
std::cout << "Contains 5: " << std::boolalpha << skipList.contains(5) << std::endl;
skipList.erase(6);
skipList.erase(2);
skipList.print(); // 输出删除元素后的跳表
return 0;
}
内存池
#include <vector>
class MemoryPool {
private:
size_t m_blockSize;
size_t m_poolSize;
char* m_memoryPool;
std::vector<bool> m_blockAvailable;
public:
MemoryPool(int blockSize, int poolSize) :m_blockSize(blockSize), m_poolSize(poolSize) {
m_memoryPool = new char[m_poolSize];
size_t blocks = m_poolSize / m_blockSize;
for (int i = 0; i < blocks; ++i) {
m_blockAvailable.push_back(true);
}
}
~MemoryPool() {
delete[]m_memoryPool;
}
void* allocate(size_t size) {
if (m_blockSize < size) {
return nullptr;
}
size_t blocks = m_poolSize / m_blockSize;
for (int i = 0; i < blocks; ++i) {
if (m_blockAvailable[i]) {
m_blockAvailable[i] = false;
return reinterpret_cast<void*>(m_memoryPool + i * m_blockSize);
}
}
return nullptr;
}
void deallocate(void* ptr) {
size_t index = (static_cast<char*>(ptr) - m_memoryPool) / m_blockSize;
if (index < m_blockAvailable.size()) {
m_blockAvailable[index] = true;
}
}
};
单例模式
class TaskQueue{
public:
TaskQueue(const TaskQueue& obj) = delete;
TaskQueue& operator=(const TaskQueue& obj) = delete;
static TaskQueue* getInstance(){
static TaskQueue taskQ;
return &taskQ;
}
void print(){
cout << "hello, world!!!" << endl;
}
private:
TaskQueue() = default;
};
int main(){
TaskQueue* queue = TaskQueue::getInstance();
queue->print();
}
类中特殊函数
#include <iostream>
class MyClass {
public:
int variable1;
int variable2;
// 默认构造函数
MyClass() {
variable1 = 0;
variable2 = 0;
std::cout << "Default constructor called" << std::endl;
}
// 析构函数
~MyClass() {
std::cout << "Destructor called" << std::endl;
}
// 拷贝构造函数
MyClass(const MyClass& other) {
variable1 = other.variable1;
variable2 = other.variable2;
std::cout << "Copy constructor called" << std::endl;
}
// 拷贝赋值运算符
MyClass& operator=(const MyClass& other) {
if (this == &other) {
return *this;
}
variable1 = other.variable1;
variable2 = other.variable2;
std::cout << "Copy assignment operator called" << std::endl;
return *this;
}
// 移动构造函数(C++11起)
MyClass(MyClass&& other) noexcept {
variable1 = other.variable1;
variable2 = other.variable2;
std::cout << "Move constructor called" << std::endl;
}
// 移动赋值运算符(C++11起)
MyClass& operator=(MyClass&& other) noexcept {
if (this == &other) {
return *this;
}
variable1 = other.variable1;
variable2 = other.variable2;
std::cout << "Move assignment operator called" << std::endl;
return *this;
}
// 其他成员函数
void printVariables() {
std::cout << "Variable 1: " << variable1 << std::endl;
std::cout << "Variable 2: " << variable2 << std::endl;
}
};
int main() {
MyClass obj1; // 默认构造函数被调用
MyClass obj2 = obj1; // 拷贝构造函数被调用
MyClass obj3(obj1); // 拷贝构造函数被调用
obj2 = obj3; // 拷贝赋值运算符被调用
MyClass obj4(std::move(obj3));// 移动构造函数被调用
obj1 = std::move(obj4); // 移动赋值运算符被调用
obj1.printVariables();
return 0;
}
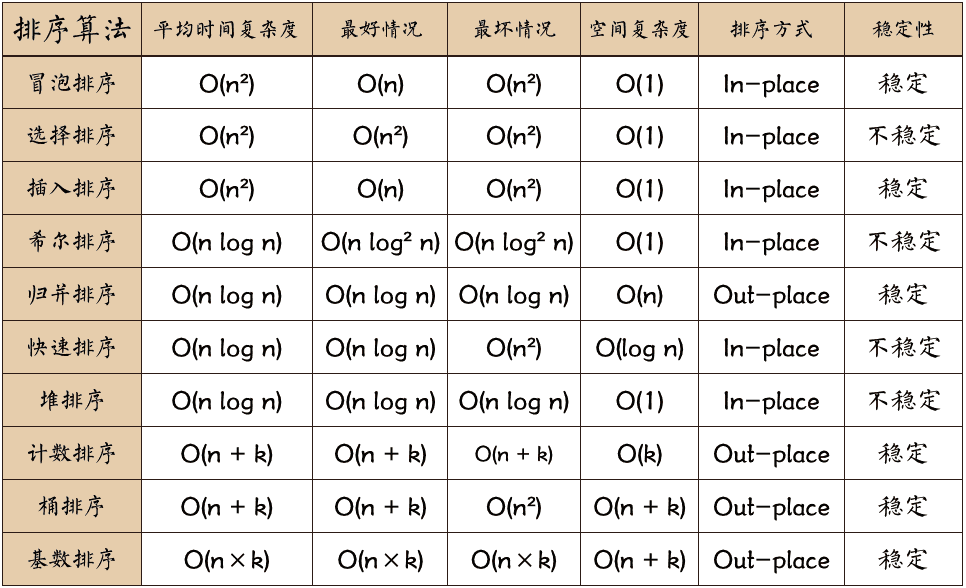
排序
选择排序
每次循环选择出最小(或最大)
void SelectSort(int a[],int length){
int tmp;
for (int i = 0; i < length; ++i){
int min = i;
for (int j = i + 1; j < length; ++j){
if (a[j] < a[min]){
min = j;
}
}
tmp = a[i];
a[i] = a[min];
a[min] = tmp;
}
}
冒泡排序
每次将元素与前面的比较,如果小就交换,然后再比较下一个
void BubbleSort(int a[], int length) {
for (int i = 0; i < length; ++i) {
for (int j = 1; j < length - i; ++j) {
if (a[j] < a[j - 1]) {
int tmp = a[j - 1];
a[j - 1] = a[j];
a[j] = tmp;
}
}
}
}
插入排序
将待排序的元素逐个插入到已经排序好的部分中的适当位置
对部分有序的数组高效
void InsertSort(int a[], int length){
int tmp;
for (int i = 1; i < length; ++i){
for (int j = i; j > 0; --j){
if (a[j] < a[j-1]){
tmp = a[j];
a[j] = a[j-1];
a[j-1] = tmp;
}
else{
break;
}
}
}
}
希尔排序
插入排序的改进,设置步长使得数据分组,分别对每组数据进行插入排序。最后改变步长,直至步长为1
void ShellSort(int a[], int length){
int step = length / 2;
int tmp;
while (step >= 1){
for (int i = step; i < length; ++i){
for (int j = i; j >= step; j -= step){
if (a[j] < a[j - step]){
tmp = a[j];
a[j] = a[j - step];
a[j - step] = tmp;
}
else{
break;
}
}
}
step = step / 2;
}
}
快排
先找一个值,通过这个值将所有元素分到它左右两边,然后对左右两边递归操作
void QuickSort(int a[], int start, int end) {
if (start >= end) {
return;
}
int left = start;
int right = end;
int target = a[start];
while (left < right) {
while (a[right] >= target && left < right) {
right--;
}
a[left] = a[right];
while (a[left] <= target && left < right) {
left++;
}
a[right] = a[left];
}
a[left] = target;
QuickSort(a, start, left - 1);
QuickSort(a, left + 1, end);
}
堆排序
堆是有序完全二叉树,节点比所有子节点都大是大堆,否则为小堆。堆的操作:
1.插入数据,将数据插在尾部,再上浮
2.删除数据,只要删除根部数据,再将尾部数据填入根部,再下沉
堆排序主要有两步,一步是建堆,一步是排序
class HeapSort{
private:
std::vector<int> heap;
int N;
public:
HeapSort(int a[],int length){
heap.push_back(0);//第一个元素不使用
for (int i = 0; i < length; ++i){
heap.push_back(a[i]);
}
N = heap.size()-1;
}
void Build(){
for (int n = N / 2; n >= 1; n--){
Sink(n);
}
}
// 排序时,是每个节点与堆顶交换,然后下沉
void Sort(){
int tmp;
while (N > 1){
tmp = heap[N];
heap[N] = heap[1];
heap[1] = tmp;
N--;
Sink(1);
}
}
// 下沉时与最大子节点交换
void Sink(int n){
int tmp;
while (2*n<=N){
int j = 2 * n;
if (j <= N-1 && heap[j] < heap[j + 1]){
j++;
}
if (heap[n] > heap[j]){
break;
}
tmp = heap[n];
heap[n] = heap[j];
heap[j] = tmp;
n = j;
}
}
};
归并排序
归并:将几个有序的数组合并为一个有序数组
归并排序:递归地使用归并
void Merge(int a[], int low, int mid, int high){
std::vector<int> tmp;
for (int i = 0; i <= high; ++i){
tmp.emplace_back(a[i]);
}
int i = low;
int j = mid + 1;
for(int h=low;h<=high;++h){
if (i > mid){
a[h] = tmp[j];
j++;
}
else if (j > high){
a[h] = tmp[i];
i++;
}
else if (tmp[i] < tmp[j]){
a[h] = tmp[i];
i++;
}
else{
a[h] = tmp[j];
j++;
}
}
}
void MergeSort(int a[],int low,int high)
{
if (low >= high) return;
int mid = (low + high) / 2;
MergeSort(a, low, mid);
MergeSort(a, mid+1, high);
Merge(a, low, mid, high);
}
B树
b树需要指定它的阶(最大分叉数),m阶b树要满足以下性质:
- 所有节点至多有m个子节点,非根非叶节点至少有ceil(m/2)个子节点
- 所有节点至多有m-1个数据,根节点至少有1个数据,其它节点至少有ceil(m/2)-1个数据
所有叶子节点都在同一层
插入操作:插入始终从底部插入,不够m-1个节点则直接插入,够了则进行分裂,把第ceil(m/2)个数据提上去
删除操作:非叶节点删除转换为叶节点删除。叶节点删除,如果节点数据不满足最低限制,要用父子替换从其左右兄弟节点借数据,如果不能借,则和兄弟节点和父节点合并
template<typename T, int M>
struct BTreeNode
{
T data[M];//多给一个位置便于之后数据的移动
BTreeNode<T, M>* children[M+1];////多给一个位置便于之后数据的移动
BTreeNode<T, M>* parent;
int size;
BTreeNode()
{
size = 0;
parent = nullptr;
for (int i=0;i<M;++i)
{
data[i] = NULL;
}
for (int i = 0; i < M+1; ++i)
{
children[i] = nullptr;
}
}
};
template<typename T,int M>
class BTree
{
private:
BTreeNode<T, M>* root;
private:
void Release(BTreeNode<T, M>* node)
{
if (node != nullptr)
{
for (int i = 0; i < M+1; ++i)
{
if (node->children[i] != nullptr)
{
Release(node->children[i]);
}
}
}
}
void Insert2Node(BTreeNode<T,M>* node, const T& v)
{
int i;
for (i = node->size-1; i >=0; --i)
{
if (v < node->data[i])
{
node->data[i + 1] = node->data[i];
}
else
{
break;
}
}
node->data[i + 1] = v;
node->size++;
}
public:
BTree()
{
root = nullptr;
}
~BTree()
{
Release(root);
}
void ShowBTree()
{
//层次遍历
std::queue<BTreeNode<T, M>*> q;
q.push(root);
ShowBTree(q);
}
void ShowBTree(std::queue<BTreeNode<T, M>*>& q)
{
std::queue<BTreeNode<T, M>*> data;
while (!q.empty())
{
int size = q.size();
for (int i = 0; i < size; ++i)
{
BTreeNode<T, M>* current = q.front();
for (int j = 0; j <= current->size; ++j)
{
if (current->children[j] != nullptr)
{
q.push(current->children[j]);
}
}
data.push(q.front());
q.pop();
}
}
while (!data.empty())
{
BTreeNode<T, M>* current = data.front();
for (int i = 0; i < current->size; ++i)
{
std::cout << current->data[i] << '\t';
}
data.pop();
}
}
void Insert(const T& v)
{
//如果是空树,直接插
if (root == nullptr)
{
root = new BTreeNode<T, M>();
root->data[0] = v;
root->size++;
return;
}
//查找插入哪个节点
BTreeNode<T, M>* current = root;
BTreeNode<T, M>* parent = nullptr;
while (current != nullptr)
{
int i;
for (i = 0; i < current->size; ++i)
{
//插入数据已存在
if (v == current->data[i])
{
break;
}
//要查找该节点的子节点
if (v < current->data[i])
{
break;
}
}
//查找子节点
parent = current;
current = current->children[i];
}
//插入到节点中
current = parent;
Insert2Node(current, v);
//节点分裂
while (true)
{
if (current->size < M)
{
break;
}
BTreeNode<T, M>* tmp1 = new BTreeNode<T, M>();
BTreeNode<T, M>* tmp2 = new BTreeNode<T, M>();
int mididx = ceil((double)M / (double)2) - 1;
int idx;
for (idx = 0; idx < mididx; ++idx)
{
tmp1->data[idx] = current->data[idx];
tmp1->children[idx] = current->children[idx];
tmp1->size++;
}
tmp1->children[idx] = current->children[idx];
for (idx = mididx + 1; idx < current->size; ++idx)
{
tmp2->data[idx - mididx - 1] = current->data[idx];
tmp2->children[idx - mididx - 1] = current->children[idx];
tmp2->size++;
}
tmp2->children[idx - mididx - 1] = current->children[idx];
tmp1->parent = current;
tmp2->parent = current;
for (int i = 0; i < tmp1->size+1; ++i)
{
if (tmp1->children[i] != nullptr)
{
tmp1->children[i]->parent = tmp1;
}
}
for (int i = 0; i < tmp2->size + 1; ++i)
{
if (tmp2->children[i] != nullptr)
{
tmp2->children[i]->parent = tmp2;
}
}
current->children[0] = tmp1;
current->children[1] = tmp2;
current->data[0] = current->data[mididx];
current->size = 1;
current->data[1] = NULL;
int i;
for (i = 2; i < M; ++i)
{
current->data[i] = NULL;
current->children[i] = nullptr;
}
current->children[i] = nullptr;
//节点合并
if (current->parent == nullptr)
{
break;
}
else
{
BTreeNode<T, M>* parent = current->parent;
int position;
for (position = parent->size-1; position >= 0; --position)
{
if (parent->data[position] < current->data[0])
{
break;
}
else
{
parent->data[position + 1] = parent->data[position];
parent->children[position + 1+1] = parent->children[position+1];
parent->children[position + 1] = parent->children[position];
}
}
parent->data[position + 1] = current->data[0];
parent->size++;
parent->children[position + 1] = current->children[0];
parent->children[position + 1 + 1] = current->children[1];
current->children[0]->parent = parent;
current->children[1]->parent = parent;
current = parent;
}
}
}
void Delete(const T& v)
{
//空树返回
if (root == nullptr)
{
return;
}
BTreeNode<T, M>* current = root;
BTreeNode<T, M>* parent = nullptr;
bool isFind = false;
//查找删除的位置
int idx;
while (current != nullptr)
{
for (idx = 0; idx < current->size; ++idx)
{
if (current->data[idx] > v)
{
break;
}
if (current->data[idx] == v)
{
isFind = true;
break;
}
}
if (isFind)
{
break;
}
parent = current;
current = current->children[idx];
}
//没有找到数据
if (!isFind)
{
return;
}
//找到了
const int MAXNUM = M - 1;//每个节点最多有m-1个数据
const int MINNUM = ceil((double)M / (double)2) - 1;//每个节点最少有ceil(M / 2) - 1个数据,根节点最少为1
//如果是非叶节点的删除,要转换为叶节点的删除
if (current->children[0] != nullptr)
{
//找前继节点
BTreeNode<T, M>* frontchild = current->children[idx];
BTreeNode<T, M>* tmpchild = nullptr;
while (frontchild != nullptr)
{
tmpchild = frontchild;
frontchild = frontchild->children[frontchild->size];
}
frontchild = tmpchild;
int tmp = frontchild->data[frontchild->size-1];
frontchild->data[frontchild->size-1] = current->data[idx];
current->data[idx] = tmp;
current = frontchild;
idx = current->size-1;
}
//对叶子节点的删除
for (int i = idx; i < current->size; ++i)
{
current->data[i] = current->data[i+1];
current->data[i + 1] = NULL;
}
current->size--;
while (true)
{
//如果是根节点,删除完成
if (current->parent == nullptr)
{
return;
}
//删除后数据满足条件
if (current->size >= MINNUM)
{
return;
}
//删除后数据不满足条件,要节点合并
//先得到该节点在父节点中的位置
int idxInParent = -1;
for (idxInParent = 0; idxInParent < (current->parent)->size + 1; ++idxInParent)
{
if ((current->parent)->children[idxInParent] == current)
{
break;
}
}
BTreeNode<T, M>* parent = current->parent;
//如果左兄弟满足,将父节点小于当前节点的最大值放入当前节点,左兄弟的最大值放入父节点
if (idxInParent - 1 >= 0)//有左兄弟
{
BTreeNode<T, M>* leftBro = parent->children[idxInParent - 1];
if (leftBro->size > MINNUM)//且左兄弟满足条件
{
Insert2Node(current, parent->data[idxInParent - 1]);
parent->data[idxInParent - 1] = leftBro->data[leftBro->size - 1];
leftBro->data[leftBro->size - 1] = NULL;
for (int i = current->size + 1; i >= 0; --i)
{
current->children[i + 1] = current->children[i];
}
if (leftBro->children[leftBro->size + 1])
{
current->children[0] = leftBro->children[leftBro->size + 1];
leftBro->children[leftBro->size + 1]->parent = current;
}
leftBro->size--;
return;
}
}
//如果右兄弟满足
if (idxInParent + 1 <= parent->size)//有右兄弟
{
BTreeNode<T, M>* rightBro = parent->children[idxInParent + 1];
if (rightBro->size > MINNUM)//且右兄弟满足条件
{
Insert2Node(current, parent->data[idxInParent]);
parent->data[idxInParent] = rightBro->data[0];
if (rightBro->children[0])
{
current->children[current->size + 1] = rightBro->children[0];
rightBro->children[0]->parent = current;
}
int i;
for (i = 1; i < rightBro->size; ++i)
{
rightBro->data[i - 1] = rightBro->data[i];
rightBro->data[i] = NULL;
rightBro->children[i - 1] = rightBro->children[i];
rightBro->children[i] = nullptr;
}
rightBro->children[i] = nullptr;
rightBro->size--;
return;
}
}
//如果都不满足,就和兄弟节点,父节点合并
while (true)
{
//如果可以和左兄弟合并
if (idxInParent - 1 >= 0)
{
BTreeNode<T, M>* leftBro = parent->children[idxInParent - 1];
leftBro->data[leftBro->size] = parent->data[idxInParent - 1];
leftBro->size++;
for (int i = 0; i < current->size; ++i)
{
leftBro->data[leftBro->size] = current->data[i];
leftBro->size++;
}
int i;
for (i = idxInParent - 1; i < parent->size; ++i)
{
parent->data[i] = parent->data[i + 1];
parent->children[i + 1] = parent->children[i + 2];
}
parent->data[i] = NULL;
parent->children[i + 1] = nullptr;
parent->size--;
break;
}
//如果可以和右兄弟合并
if (idxInParent + 1 <= parent->size)
{
BTreeNode<T, M>* rightBro = parent->children[idxInParent + 1];
//将右节点数据统一后移1+current->size个位置
int offset = 1 + current->size;
for (int i = rightBro->size; i >= 0; --i)
{
rightBro->data[i + offset] = rightBro->data[i];
rightBro->children[i + offset] = rightBro->children[i];
}
rightBro->data[offset - 1] = parent->data[idxInParent];
rightBro->size++;
int i;
for (i = current->size - 1; i >= 0; --i)
{
rightBro->data[i] = current->data[i];
rightBro->children[i + 1] = current->children[i + 1];
rightBro->size++;
}
rightBro->children[0] = current->children[0];
if (current->children[0])
{
current->children[0]->parent = rightBro;
}
for (i = idxInParent; i < parent->size; ++i)
{
parent->data[i] = parent->data[i + 1];
parent->children[i] = parent->children[i + 1];
}
parent->children[i] = parent->children[i + 1];
parent->data[i] = NULL;
parent->children[i + 1] = nullptr;
parent->size--;
break;
}
}
//合并父节点后,要再循环,看父节点是否满足条件
//清除这一节点
BTreeNode<T, M>* tmp = current;
current = current->parent;
for (int i = 0; i < M; ++i)
{
tmp->data[i] = NULL;
tmp->children[i] = nullptr;
}
tmp->parent = nullptr;
tmp->size = 0;
//如果是根,只要有数据就行
if (current == root)
{
if (current->size > 0)
{
return;
}
root = current->children[0];
current->children[0]->parent = nullptr;
return;
}
}
}
};
红黑树
非严格意义上的平衡二叉树,所以它的左右子树高度可能超过1。但它的平衡性指到从根达所有叶子节点的路径都包含相同的黑色节点。因此它表现的性质为:
- 所有节点要么是黑,要么是红,根节点必须是黑,叶子节点必须是黑且是空(一般也不画出来)
- 红色节点都不相邻
- 相比AVL,红黑树调整平衡的旋转少,甚至只需要调整颜色,所以删除插入更快,但搜索上可能AVL更快
插入操作:
- 插入节点的父节点为黑,不用调整
- 插入节点的父节点和父节点的兄弟节点都为红:父节点及其兄弟节点变黑,爷爷节点变红
- 插入节点的父节点为红,父节点的兄弟节点为黑或没有,则旋转,之后变色,爷爷节点变红,父节点变黑
删除操作:
- 删除节点有左右子树,将其用后继节点代替,就转化为以下两种
- 删除节点只有左子树或右子树(该节点一定为黑),直接让孩子代替并变黑
- 删除节点是叶子节点,红的话直接删除,黑的
应用:
- 广泛用于C++中,map和set用红黑树实现的
- Linux的的进程调度,用红黑树管理进程控制块,进程的虚拟内存空间都存储在一颗红黑树上,每个虚拟内存空间都对应红黑树的一个结点,左指针指向相邻的虚拟内存空间,右指针指向相邻的高地址虚拟内存空间
- IO多路复用的epoll采用红黑树组织管理sockfd,以支持快速的增删改查
- Nginx中用红黑树管理定时器,因为红黑树是有序的,可以很快的得到距离当前最小的定时器
template<typename T>
class RBTreeNode
{
public:
T data;
RBTreeNode* leftchild;
RBTreeNode* rightchild;
RBTreeNode* parent;
bool isred;
};
template<typename T>
class RBTree
{
private:
RBTreeNode<T>* root;
private:
void Release(RBTreeNode<T>* node)
{
if (node != nullptr)
{
Release(node->rightchild);
Release(node->leftchild);
}
delete node;
}
int Getlevel(RBTreeNode<T>* node)
{
int level = 1;//根节点是第一层
while (node->parent)
{
level++;
node = node->parent;
}
return level;
}
public:
RBTree()
{
root = nullptr;
}
~RBTree()
{
Release(root);
}
void Show()
{
std::deque<RBTreeNode<T>*> q;
RBTreeNode<T>* frontNode;
int level;
int currentLvele = 1;
q.push_back(root);
while (!q.empty())
{
frontNode = q.front();
q.pop_front();
level = Getlevel(frontNode);
if (currentLvele !=level )
{
std::cout << '\n';
currentLvele = level;
}
std::cout << frontNode->data << (frontNode->isred == true ? 'r' : 'b') << '\t';
if (frontNode->leftchild)
{
q.push_back(frontNode->leftchild);
}
if (frontNode->rightchild)
{
q.push_back(frontNode->rightchild);
}
}
}
void Insert(const T& data)
{
Insert(root, data);
//最后将根变为黑
root->isred = false;
}
void Insert(RBTreeNode<T>*& node, const T& data)
{
RBTreeNode<T>* current = node;
RBTreeNode<T>* parent = nullptr;
//先找插入的位置
while (current)
{
//不允许插入相同值
if (current->data == data)
{
return;
}
parent = current;
if (current->data > data)
{
current = current->leftchild;
}
else
{
current = current->rightchild;
}
}
current = parent;
//插入数据
RBTreeNode<T>* newNode = new RBTreeNode<T>();
newNode->data = data;
newNode->isred = true;
newNode->leftchild = nullptr;
newNode->rightchild = nullptr;
newNode->parent = current;
//如果是空树,直接插入黑色节点,插入完成
if (!current)
{
root = newNode;
newNode->isred = false;
return;
}
//不是空树就要进行平衡操作
//先插入
if (current->data > data)
{
current->leftchild = newNode;
}
else
{
current->rightchild = newNode;
}
//平衡调整
//插入节点的父亲是黑色,不用调整
if (current->isred == false)
{
return;
}
//否则父节点为红色,要调整
Balance(newNode, current);
}
void Balance(RBTreeNode<T>*& newNode,RBTreeNode<T>*& parent)
{
RBTreeNode<T>* parentBro = nullptr;
RBTreeNode<T>* grandParent = nullptr;
while (true)
{
//得到爷爷节点
if (parent->parent)
{
grandParent = parent->parent;
}
else
{
break;
}
//得到兄弟节点
if (grandParent->leftchild == parent)
{
if (grandParent->rightchild)
{
parentBro = grandParent->rightchild;
}
else
{
parentBro = nullptr;
}
}
else
{
if (grandParent->leftchild)
{
parentBro = grandParent->leftchild;
}
else
{
parentBro = nullptr;
}
}
//如果兄弟节点为空或者为黑色要进行旋转
if (parentBro == nullptr || parentBro->isred == false)
{
//只右转
if (parent == grandParent->leftchild && newNode == parent->leftchild)
{
TurnRight(grandParent, parent);
}
//只左转
else if (parent == grandParent->rightchild && newNode == parent->rightchild)
{
TurnLeft(grandParent, parent);
}
//这是要进行两次旋转的情况
else
{
//先右再左
if (newNode == parent->leftchild)
{
TurnRight(parent,newNode);
parent = newNode;
TurnLeft(grandParent, parent);
}
//先左再右
else
{
TurnLeft(parent, newNode);
parent = newNode;
TurnRight(grandParent, parent);
}
}
//调整颜色
parent->isred = false;
grandParent->isred = true;
}
//如果兄弟节点为红色,只要变颜色parentBro->isred == true
else
{
parent->isred = false;
parentBro->isred = false;
grandParent->isred = true;
}
//如果parent的父节点为空,说明是根节点,结束即可
if (parent->parent == nullptr)
{
break;
}
//重新向上迭代
newNode = parent->parent;
if (parent->parent->parent)
{
parent = parent->parent->parent;
}
else
{
break;
}
}
}
void TurnLeft(RBTreeNode<T>*& grandParent, RBTreeNode<T>*& parent)
{
grandParent->rightchild = parent->leftchild;
if (parent->leftchild)
{
parent->leftchild->parent = grandParent;
}
parent->leftchild = grandParent;
if (grandParent->parent)
{
parent->parent = grandParent->parent;
if (grandParent->parent->leftchild == grandParent)
{
grandParent->parent->leftchild = parent;
}
else
{
grandParent->parent->rightchild = parent;
}
}
//说明到了根
else
{
parent->parent = nullptr;
root = parent;
}
grandParent->parent = parent;
}
void TurnRight(RBTreeNode<T>*& grandParent, RBTreeNode<T>*& parent )
{
grandParent->leftchild = parent->rightchild;
if (parent->rightchild)
{
parent->rightchild->parent = grandParent;
}
parent->rightchild = grandParent;
if (grandParent->parent)
{
parent->parent = grandParent->parent;
if (grandParent->parent->leftchild == grandParent)
{
grandParent->parent->leftchild = parent;
}
else
{
grandParent->parent->rightchild = parent;
}
}
//说明到了根
else
{
parent->parent = nullptr;
root = parent;
}
grandParent->parent = parent;
}
};
哈希表
基于拉链的哈希/散列表
class HashNode
{
public:
int key;
int data;
HashNode* next{ nullptr };
HashNode(int key, int data):key(key),data(data){}
};
class HashTableLink
{
private:
std::vector<HashNode*> table;
int size;
public:
HashTableLink(int size) :size(size)
{
for (int i = 0; i < size; ++i)
{
table.push_back(NULL);
}
}
void Insert(int key, int data)
{
HashNode *node=new HashNode(key, data);
node->next = table[key % size];
table[key % size] = node;
}
void Delete(int key)
{
HashNode* node = table[key % size];
if (!node)
{
return;
}
if (node->key == key)
{
table[key % size] = node->next;
return;
}
HashNode* n = node->next;
HashNode* p = node;
while (n)
{
if (n->key == key)
{
p->next = n->next;
}
p = n;
n = n->next;
}
}
int Get(int key)
{
HashNode* node = table[key % size];
int result=NULL;
while (node)
{
if (node->key == key)
{
result = node->data;
break;
}
else
{
node = node->next;
}
}
return result;
}
};
基于开放地址/线性探测的哈希表
class HashTableLiner
{
private:
int size{ 0 };
int capcity;
std::vector<int> keyTable;
std::vector<int> valueTable;
public:
HashTableLiner(int capcity):capcity(capcity)
{
keyTable.resize(capcity);
valueTable.resize(capcity);
}
void Insert(int key,int value)
{
for (int i = key % capcity; i < capcity; ++i)
{
if (!keyTable[i])
{
keyTable[i] = key;
valueTable[i] = value;
size++;
break;
}
else
{
//相同key值更新value
if (key == keyTable[i])
{
valueTable[i] = value;
break;
}
}
}
//扩容
if (size >= capcity / 2)
{
capcity = capcity * 2;
std::vector<int> tmpKey = keyTable;
std::vector<int> tmpValue = valueTable;
keyTable.clear();
keyTable.resize(capcity);
valueTable.clear();
valueTable.resize(capcity);
size = 0;
for (int i = 0; i < tmpKey.size(); ++i)
{
if (tmpKey[i])
{
Insert(tmpKey[i], tmpValue[i]);
}
}
}
}
void Delete(int key)
{
for (int i = key % capcity; i < capcity; ++i)
{
if (!keyTable[i])
{
return;
}
if (key == keyTable[i])
{
keyTable[key % capcity] = NULL;
valueTable[key % capcity] = NULL;
size--;
break;
}
}
for (int i = key % capcity+1; i < capcity; ++i)
{
if (keyTable[i])
{
int tmp1 = keyTable[i];
keyTable[i] = NULL;
int tmp2 = valueTable[i];
valueTable[i] = NULL;
size--;
Insert(tmp1, tmp2);
}
else
{
break;
}
}
}
int Get(int key)
{
int result = NULL;
for (int i = key % capcity; i < capcity; ++i)
{
if (!keyTable[i])
{
break;
}
if (keyTable[i] == key)
{
result=valueTable[i];
break;
}
}
return result;
}
};
图
//基于邻接表实现的无向图
struct GNode
{
int value;
GNode* next;
GNode(int value):value(value),next(nullptr){}
};
class Graph
{
private:
int V;
int E;
std::map<int,GNode*> adj;
public:
Graph(int V):V(V),E(0)
{
}
void AddVertex(int v)
{
adj[v] = nullptr;
V++;
}
void AddEdge(int v1, int v2)
{
GNode *node = adj[v1];
if (node == nullptr)
{
adj[v1] = new GNode(v2);
}
else
{
while (node->next != nullptr)
{
node = node->next;
}
node->next = new GNode(v2);
}
node = adj[v2];
if (node == nullptr)
{
adj[v2] = new GNode(v1);
}
else
{
while (node->next != nullptr)
{
node = node->next;
}
node->next = new GNode(v1);
}
E++;
}
void DeleteEdge(int v1, int v2)
{
GNode* node;
GNode* per;
if (adj[v1]->value == v2)
{
adj[v1] = adj[v1]->next;
}
else
{
node = adj[v1];
per = node;
while (node->value != v2)
{
per = node;
node = node->next;
}
per->next = node->next;
}
if (adj[v2]->value == v1)
{
adj[v2] = adj[v2]->next;
}
else
{
node = adj[v2];
per = node;
while (node->value != v1)
{
per = node;
node = node->next;
}
per->next = node->next;
}
E--;
}
//深度广度优先遍历
void DFS(int v)
{
std::vector<bool> marked(V, false);
int count = 0;
dfs(v,marked,count);
if (count != V)
{
std::cout << "不连通\n";
}
}
void dfs(int v, std::vector<bool>& marked,int &count)
{
marked[v] = true;
std::cout << v;
count++;
GNode* node = adj[v];
while (node != nullptr)
{
if (marked[node->value] != true)
{
dfs(node->value, marked, count);
}
node = node->next;
}
}
void BFS(int v)
{
std::vector<bool> marked(V, false);
int count = 0;
std::queue<int> q;
q.push(v);
marked[v] = true;
GNode* node;
while (!q.empty())
{
node = adj[q.front()];
std::cout << q.front() << '\n';
while (node)
{
if (marked[node->value] != true)
{
marked[node->value] = true;
q.push(node->value);
}
node = node->next;
}
q.pop();
}
}
};
最小生成树
边的权值的和最小的树。针对无向连通权重图:Prim与Kruskal
Kruskal算法是一种贪心算法,具体步骤如下:
- 将图中的所有边按照权重进行排序
- 从权重最小的边开始,依次选择边,但要确保选择的边不会形成环路。如果形成环路,则不选择该边
- 重复步骤2,直到选择了n-1条边,其中n是图中顶点的数量
Prim算法也是一种贪心算法,具体步骤如下:
- 初始化一个空的最小生成树,选择一个起始顶点
- 将起始顶点加入最小生成树中,并标记为已访问
- 重复以下步骤,直到最小生成树包含了图中的所有顶点:
- 在已访问的顶点中选择一个顶点v和一个未访问的顶点u,使得v到u的边的权重最小
- 将顶点u加入最小生成树中,并将边(v, u)加入最小生成树的边集合中。
- 标记顶点u为已访问
//union-find算法
class UnionFind
{
private:
int V;
std::vector<int> parent;
std::vector<int> size;//用于平衡
public:
UnionFind(int v) :V(v)
{
for (int i = 0; i < V; ++i)
{
parent.push_back(i);
size.push_back(1);
}
}
int GetRoot(int v)
{
while (parent[v] != v)
{
parent[v] = parent[parent[v]];//用于路径压缩
v = parent[v];
}
return v;
}
void Union(int v1, int v2)
{
v1 = GetRoot(v1);
v2 = GetRoot(v2);
if (size[v1] <= size[v2])
{
parent[v2] = v1;
size[v1] = size[v1] + size[v2];
}
else
{
parent[v1] = v2;
size[v2] = size[v2] + size[v1];
}
}
bool Connect(int v1, int v2)
{
v1 = GetRoot(v1);
v2 = GetRoot(v2);
if (v1 != v2)
{
return false;
}
else
{
return true;
}
}
};
class Edge
{
public:
int v1;
int v2;
int weight;
Edge* next{nullptr};
Edge() = default;
Edge(int v1,int v2,int weight):v1(v1),v2(v2),weight(weight){}
};
struct great {
bool operator() (const Edge& x, const Edge& y) const
{
return x.weight > y.weight;
}
};
class WGraph
{
private:
int V{ 0 };
int E{ 0 };
std::map<int, Edge*> adj;
public:
void Insert(int v1, int v2, int weight)
{
E = E + 1;
if (adj.find(v1) == adj.end())
{
V = V + 1;
}
if (adj.find(v2) == adj.end())
{
V = V + 1;
}
Edge *e1=new Edge(v1, v2, weight);
e1->next = adj[v1];
adj[v1]=e1;
Edge *e2=new Edge(v1, v2, weight);
e2->next = adj[v2];
adj[v2] = e2;
}
void Kruskal()
{
std::vector<bool> marked(V, false);
std::priority_queue<Edge, std::vector<Edge>, great> pQueue;
std::queue<Edge> q;
for (int i = 0; i<adj.size(); ++i)
{
Edge* e = adj[i];
if (i == e->v1)
{
pQueue.push(*e);
}
while (e->next != nullptr)
{
e = e->next;
if (i==e->v1)
{
pQueue.push(*e);
}
}
}
Edge minE;
UnionFind ufind(V);
while (!pQueue.empty())
{
minE = pQueue.top();
pQueue.pop();
if (ufind.Connect(minE.v1, minE.v2))
{
continue;
}
else
{
ufind.Union(minE.v1, minE.v2);
q.push(minE);
}
}
while (!q.empty())
{
std::cout << q.front().v1 << '\t' << q.front().v2 << '\t' << q.front().weight << '\n';
q.pop();
}
}
void Prim(int v)
{
std::vector<bool> marked(V, false);
std::priority_queue<Edge, std::vector<Edge>, great> pQueue;
std::queue<Edge> q;
marked[v] = true;
Edge *e = adj[v];
pQueue.push(*e);
while (e->next!=nullptr)
{
e = e->next;
pQueue.push(*e);
}
while (!pQueue.empty())
{
Edge minE = pQueue.top();
pQueue.pop();
if (marked[minE.v1] && marked[minE.v2])
{
continue;
}
q.push(minE);
if (!marked[minE.v1])
{
marked[minE.v1] = true;
e = adj[minE.v1];
pQueue.push(*e);
while (e->next != nullptr)
{
e = e->next;
pQueue.push(*e);
}
}
if (!marked[minE.v2])
{
marked[minE.v2] = true;
e = adj[minE.v2];
pQueue.push(*e);
while (e->next != nullptr)
{
e = e->next;
pQueue.push(*e);
}
}
}
while (!q.empty())
{
std::cout<<q.front().v1<<'\t' << q.front().v2<<'\t' << q.front().weight<<'\n';
q.pop();
}
}
};
最短路径
Dijkstra算法:处理路径不是负值的图,解决单源最短路径问题(找一个点到其它点的最短路径)
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
struct compare {
bool operator()(vector<int> a, vector<int> b) {
return a[1] > b[1];
}
};
int main() {
int n = 9;
vector<vector<int>> g = {
{0,4,-1,-1,-1,-1,-1,8,-1},
{4,0,8,-1,-1,-1,-1,11,-1},
{-1,8,0,7,-1,4,-1,-1,2},
{-1,-1,7,0,9,14,-1,-1,-1},
{-1,-1,-1,9,0,10,-1,-1,-1},
{-1,-1,4,14,10,0,2,-1,-1},
{-1,-1,-1,-1,-1,2,0,1,6},
{8,11,-1,-1,-1,-1,1,-1,7},
{-1,-1,2,-1,-1,-1,6,7,0}
};
vector<int> pre(9);
vector<int> path(9, INT_MAX);
vector<int> visit(9, false);
priority_queue <vector<int>, vector<vector<int>>, compare> q;
path[0] = 0;
q.push(vector<int>{ 0,0 });// 到0点的路程为0
while (!q.empty()) {
int start = q.top()[0];
q.pop();
if (visit[start]) {
continue;
}
for (int i = 0; i < n; ++i) {
if (g[start][i] == -1 || g[start][i] == 0) {
continue;
}
if (visit[i]) {
continue;
}
if (path[start] + g[start][i] < path[i]) {
path[i] = path[start] + g[start][i];
pre[i] = start;
q.push(vector<int>{ i, path[i] });
}
}
visit[start] = true;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号