15. 多层感知机原理及实现
多层感知机及代码实现
完整的实验代码在我的github上👉QYHcrossover/ML-numpy: 机器学习算法numpy实现 (github.com) 欢迎star⭐
多层感知机(MLP)是一种前馈神经网络,由输入层、若干个隐藏层和输出层组成。每一层都由多个神经元组成。MLP一般用于分类问题,可以通过反向传播算法进行训练。在深度学习领域,MLP是一种基础结构,被广泛应用于图像识别、自然语言处理等领域。
多层感知机的结构
多层感知机的结构如下图所示:
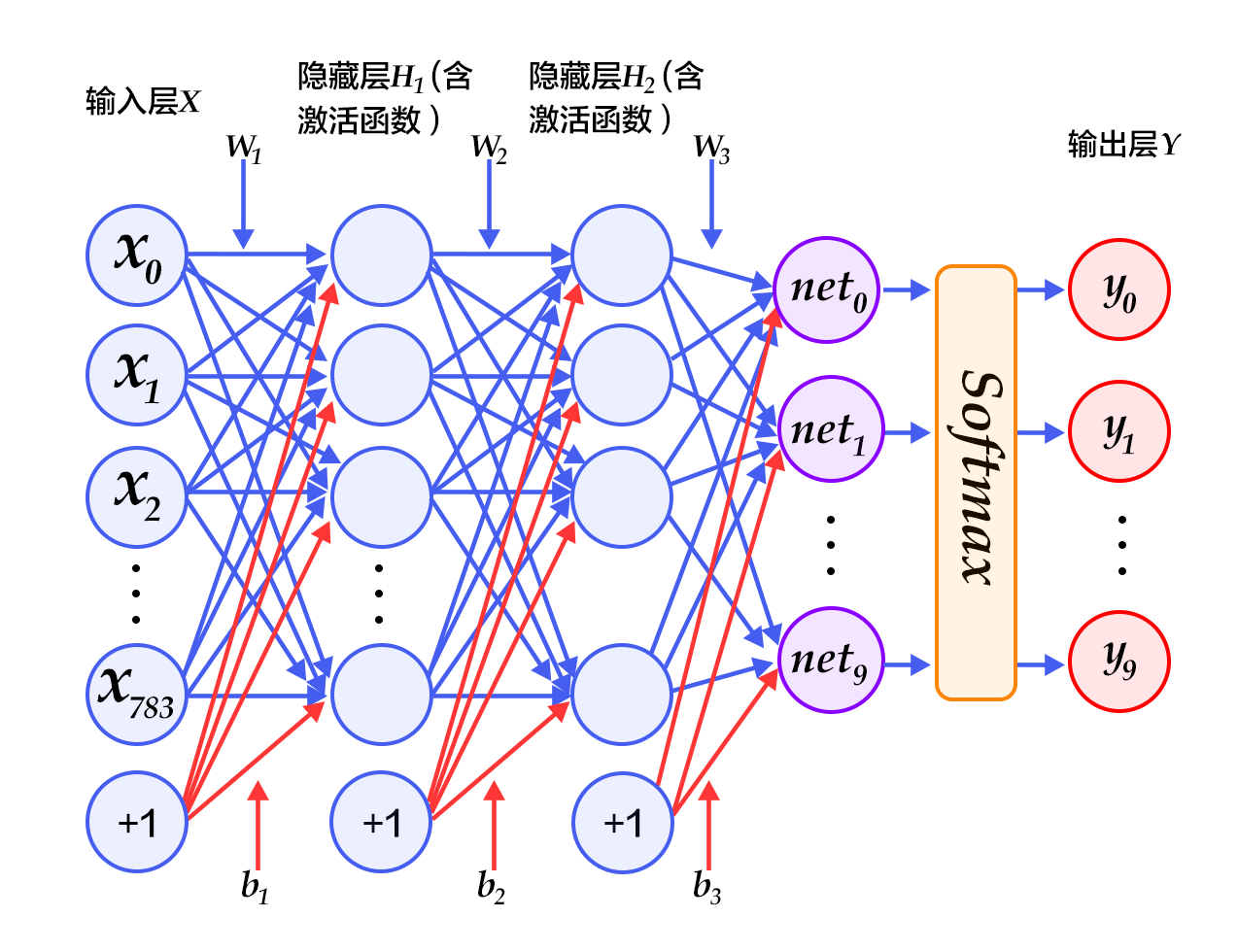
其中,输入层接受输入数据,隐藏层通过激活函数将输入数据进行非线性变换,输出层将隐藏层输出映射到目标空间,得到预测结果。在训练过程中,可以通过反向传播算法将预测结果与真实标签进行比对,求得误差并更新模型参数。
多层感知机原理
激活函数
在多层感知机中,激活函数用于将输入数据进行非线性变换。常用的激活函数有sigmoid函数、ReLU函数、tanh函数等。
其中,sigmoid函数定义如下:
$$sigmoid(x) = \frac{1}{1+e^{-x}}$$
ReLU函数定义如下:
$$ReLU(x) = max(0,x)$$
tanh函数定义如下:
$$tanh(x) = \frac{ex-e{-x}}{ex+e{-x}}$$
前向传播
在多层感知机中,前向传播用于将输入数据传递至输出层。设输入数据为$x$,第$i$层隐藏层的输出为$h_i(x)$,第$l$层隐藏层到第$l+1$层隐藏层之间的权重矩阵为$W_{l}$,第$l$层隐藏层的偏置为$b_l$,则前向传播的计算过程如下:
$$h_1(x) = f(W_1x+b_1)$$
$$h_l(x) = f(W_lh_{l-1}(x)+b_l)$$
$$y(x) = f(W_{L}h_{L-1}(x)+b_{L})$$
其中,$f$为激活函数,$W_{L}$为输出层权重矩阵,$b_{L}$为输出层偏置。
反向传播
在多层感知机中,反向传播用于更新模型参数,求解损失函数的梯度。设损失函数为$L$,输出为$y$,真实标签为$t$,则反向传播的计算过程如下:
$$\delta_{L} = \frac{\partial L}{\partial y}f'(W_{L}h_{L-1}(x)+b_{L})$$
$$\delta_{l} = \frac{\partial L}{\partial h_{l}}f'(W_{l+1}^{T}\delta_{l+1})$$
$$\frac{\partial L}{\partial W_{l}} = h_{l-1}\delta_{l}^{T}$$
$$\frac{\partial L}{\partial b_{l}} = \delta_{l}$$
其中,$\delta_{L}$为输出层误差,$\delta_{l}$为第$l$层隐藏层误差,$f'$为激活函数的导数。
损失函数
在多层感知机中,常用的损失函数有均方误差(MSE)和交叉熵(cross-entropy)。
均方误差损失函数定义如下:
$$MSE(y,t) = \frac{1}{n}\sum_{i=1}{n}(y_i-t_i)2$$
交叉熵损失函数定义如下:
$$CE(y,t) = -\sum_{i=1}^{n}t_i\log(y_i)$$
其中,$n$为样本数,$y$为模型预测结果,$t$为真实标签。
多层感知机的代码实现
下面是我自己手动使用python和numpy实现的多层感知机模型
import numpy as np
import math
class MLP:
def __init__(self,units,activs):
self.units = units
self.length = len(units)
self.activations = activs
assert len(units)-1 == len(activs) and set(activs).issubset(set(["noactiv","relu","sigmoid","softmax","tanh"])) and "softmax" not in activs[:-1]
#构造激活函数和激活函数的导数
activDict,derivDict = MLP.Activations()
#!默认第0除了A[0]也就是X外,其他W,b,g都是None
self.activs = [None]+[activDict[i] for i in activs]
self.derivs = [None]+[derivDict[i] if i!="softmax" else None for i in activs]
#随机初始化W和b
self.Ws = [None]+[2*np.random.random([units[i+1],units[i]])-1 for i in range(0,len(units)-1)]
self.bs = [None]+[np.zeros([units[i+1],1]) for i in range(0,len(units)-1)]
#激活函数与其导数
def Activations():
#激活函数
noactiv = lambda x:x
sigmoid = lambda x: 1/(1+np.exp(-x))
relu = lambda x: 1*(x>0)*x
softmax = lambda x:np.exp(x)/np.sum(np.exp(x),axis=0)
tanh = lambda x: (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
activations = {"noactiv":noactiv,"sigmoid":sigmoid,"relu":relu,"softmax":softmax,"tanh":tanh}
#激活函数的导数
noactiv_d = lambda x:np.ones_like(x)
sigmoid_d = lambda x: sigmoid(x)*(1-sigmoid(x))
relu_d = lambda x: 1*(x>0)
tanh_d = lambda x: 1-tanh(x)**2
'''定义的softmax的导数,在实际中常与交叉熵函数结合起来求导
且下面的公式只适合单个样本,多个样本下涉及矩阵对矩阵的求导比较麻烦
def softmax_d(x):
y = MLP.softmax(x)
temp = -1*y@y.T
print(temp)
for i in range(x.shape[0]):
temp[i][i] += y[i].squeeze()
return temp
'''
derivatives = {"noactiv":noactiv_d,"sigmoid":sigmoid_d,"relu":relu_d,"tanh":tanh_d}
return activations,derivatives
#前向传播
def forward(self,X):
#同时记录Z和A
Zs,As = [None]*self.length,[None]*self.length
#初始化A[0]为X
As[0] = X
#逐层计算
for i in range(1,self.length):
Zs[i] = self.Ws[i]@As[i-1] + self.bs[i]
As[i] = self.activs[i](Zs[i])
return Zs,As
#反向传播
def backward(self,X,Y,lr,loss_function):
amount = X.shape[-1] #样本数量
Zs,As = self.forward(X)
loss = loss_function.calLoss(As[-1],Y)
if self.activations[-1] == "softmax":
dZ = As[-1] - Y
else:
dA = loss_function.calDeriv(As[-1],Y)
for l in range(self.length-1,0,-1):
#分别计算dZ,dW,db,dA
if self.activations[-1]!="softmax" or l<self.length-1:
dZ = dA * self.derivs[l](Zs[l])
dW = 1/amount * dZ @ As[l-1].T
db = 1/amount * np.sum(dZ,axis=1,keepdims=True)
dA = self.Ws[l].T @ dZ
#梯度下降
self.Ws[l] -= lr*dW
self.bs[l] -= lr*db
return loss
#主函数
def fit(self,X,Y,lr,max_iters,loss_function,batch_size=None):
#X,y,units是神经网络个数,activations为激活函数列表,loss为损失函数以及导数计算方式
assert X.shape[-1] == self.units[0] and Y.shape[-1] == self.units[-1] #第一维和最后一维需要匹配
#为了不将转置施加于W和b上,故将X和Y转置
X,Y = X.T,Y.T
amount = X.shape[-1] #样本数量
#开始迭代
for epoch in range(max_iters):
#batch梯度下降或minibatch梯度下降
if not batch_size:
loss_avg = self.backward(X,Y,lr,loss_function)
else:
loss_avg = 0
for i in range(math.ceil(amount/batch_size)):
loss = self.backward(X[:,i*batch_size:i*batch_size+batch_size],Y[:,i*batch_size:i*batch_size+batch_size],lr,loss_function)
loss_avg = (i/(i+1))*loss_avg +(1/(i+1))*loss
print("第{}轮训练,loss大小为{}".format(epoch,loss_avg))
#损失函数的模板类,该类定义了两个方法分别是
#计算loss和根据loss计算导数、该类必须被实体类继承
class LossFunc:
def calLoss(y,y_h):
pass
def calDeriv(y,y_h):
pass
if __name__ == "__main__":
# ##例子一、分类模型,mnist的例子
# #载入数据集
# X_train = np.load(r"..\SVM\之前\X_train.npy")
# y_train = np.load(r"..\SVM\之前\y_train.npy")
# #将y_train进行one-hot编码
# def one_hot(y,feature_size):
# LB = np.zeros([len(y), feature_size], dtype=np.int32)
# for i in range(len(y)):
# LB[i][y[i]] = 1
# return LB
# y_train = one_hot(y_train,10)
# #构建交叉熵损失函数
# class CrossEntropy(LossFunc):
# def calLoss(y,y_h):
# return np.mean(np.sum(-1*y_h*np.log(y),axis=0))
# #构建模型
# mlp = MLP([784,50,50,10],["tanh","tanh","softmax"])
# mlp.fit(X_train,y_train,0.1,10000,CrossEntropy,batch_size=None)
# '''
#例子二,线性回归的例子,波士顿房价预测
import sklearn.datasets as datasets
boston = datasets.load_boston()
#构建均方误差损失函数
class MSE(LossFunc):
def calLoss(y,y_h):
return np.mean(np.sum((y - y_h)**2,axis=0))
def calDeriv(y,y_h):
return 2*(y-y_h)
mlp = MLP([13,5,5,1],["relu","relu","noactiv"])
mlp.fit(boston.data,boston.target[:,np.newaxis],0.01,3000,MSE,batch_size=None)
构造函数
init(self,units,activs)
- units:一个列表,表示每一层的神经元个数。
- activs:一个列表,表示每一层的激活函数。默认第一层没有激活函数。
激活函数与激活函数的导数
Activations()
- 返回激活函数与激活函数的导数。
前向传播
forward(self,X)
- X:输入数据。
- 返回每一层的加权和与激活后的输出。
反向传播
backward(self,X,Y,lr,loss_function)
- X:输入数据。
- Y:真实标签。
- lr:学习率。
- loss_function:损失函数。
- 返回损失。
训练函数
fit(self,X,Y,lr,max_iters,loss_function,batch_size=None)
- X:输入数据。
- Y:真实标签。
- lr:学习率。
- max_iters:最大迭代次数。
- loss_function:损失函数。
- batch_size:批量梯度下降和小批量梯度下降的批量大小。默认为 None,表示全量梯度下降。
损失函数
损失函数是一个模板类,需要被实体类继承。模板类中定义了两个方法:
calLoss(y,y_h):计算损失。
calDeriv(y,y_h):根据损失计算导数。
示例代码
代码实现了两个示例:分类模型和线性回归模型。分类模型使用了交叉熵损失函数,线性回归模型使用了均方误差损失函数。
结论
多层感知机是一种前馈神经网络,由输入层、若干个隐藏层和输出层组成。在深度学习领域,MLP是一种基础结构,被广泛应用于图像识别、自然语言处理等领域。可以使用Python和PyTorch库实现简单的MLP,用于对各种分类问题进行处理。
完整的实验代码在我的github上👉QYHcrossover/ML-numpy: 机器学习算法numpy实现 (github.com) 欢迎star⭐



