入坑 可持久化线段树——主席树

主席树主要用来处理历史版本查询。
这一篇我只想想先说说对于区间Kth的处理。
如果把区间的每一位都视为一次更新（可以视为数据在0～inf范围的一次更新）求区间Kth就转变为某个元素在某段历史中出现的Kth那么一个值是多少。
每次修改，有别于普通线段数，完全新造一棵树（时空间都不允许）。
这也就是主席树有别于于普通线段数的地方：每次修改都是在原来的基础上，加了一条链。

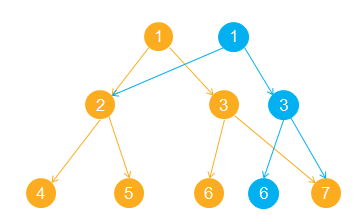
对于没更新的子节点，连接到原来的节点，而新插入的值造个新节点就好了。
对于网上除了LadyLex的鲜有指针版的板子，那我写个指针版（现学现卖。。）好了。
递归版

inline void insert(tree* pre,tree* &x,int l,int r)
    {
        x->ch[0]=pre->ch[0];
        x->ch[1]=pre->ch[1];
        x->sum=pre->sum+1;
        if(l==r)return;
        int mid=(l+r)>>1;
        if(pos<=mid)insert(pre->ch[0],x->ch[0],l,mid);
        else insert(pre->ch[1],x->ch[1],mid+1,r);
    }

也可以写个二分（略）
然后，把主席树建成权值线段树，维护区间元素的总个数，就可以用来求Kth了。
想一想为什么。
因为已经把区间每个位置当做一个新的版本了，新建了n条链。可以看出它具有区间可减行。很容易确定我们要找的区间左右端点所指向的root，维护了权值区间元素的个数，也就很容易找到这个区间的kth。（先判断左子区间元素个数。。以此类推）
这次我写了个二分版

    inline int q(tree* x1,tree* x2,int k,int l,int r)
    {
        while(l<r)
        {
            int cmp=(x2->ch[0]->sum-x1->ch[0]->sum),mid=(l+r)>>1;
            if(cmp>=k)x2=x2->ch[0],x1=x1->ch[0],r=mid;
            else x2=x2->ch[1],x1=x1->ch[1],l=mid+1,k-=cmp;
        }
        return b[r];
    }

完整的板子（poj2104）
这个板子对数据进行了离散，其实因为是动态开点，不离散也是没问题的。（20w的区间长，-inf~inf都没问题）

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 100005
using namespace std;
int n,m,pos,a[N],b[N];
namespace chairtree
{
    struct tree
    {
        tree* ch[2];int sum;
        tree(){sum=0;ch[0]=ch[1]=NULL;}
    }*root[N],*null=new tree();
    inline tree* newtree()
    {
        tree *o=new tree();
        o->ch[0]=o->ch[1]=null;
        return o;
    }
    inline void insert(tree* pre,tree* &x,int l,int r)
    {
        x->ch[0]=pre->ch[0];
        x->ch[1]=pre->ch[1];
        x->sum=pre->sum+1;
        if(l==r)return;
        int mid=(l+r)>>1;
        if(pos<=mid)insert(pre->ch[0],x->ch[0],l,mid);
        else insert(pre->ch[1],x->ch[1],mid+1,r);
    }
    inline int q(tree* x1,tree* x2,int k,int l,int r)
    {
        while(l<r)
        {
            int cmp=(x2->ch[0]->sum-x1->ch[0]->sum),mid=(l+r)>>1;
            if(cmp>=k)x2=x2->ch[0],x1=x1->ch[0],r=mid;
            else x2=x2->ch[1],x1=x1->ch[1],l=mid+1,k-=cmp;
        }
        return b[r];
    }
}
using namespace chairtree;
int main()
{
    scanf("%d%d",&n,&m);
    null->ch[0]=null;null->ch[1]=null;
    for(int i=1;i<=n;i++)scanf("%d",&a[i]),b[i]=a[i],root[i]=newtree();
    sort(b+1,b+n+1);
    root[0]=newtree();
    for(int i=1;i<=n;i++)
    {
        pos=lower_bound(b+1,b+n+1,a[i])-b;
        insert(root[i-1],root[i],1,n);
    }
    int l,r,k;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&l,&r,&k);
        printf("%d\n",q(root[l-1],root[r],k,1,n));
    }
}

但是这样的主席树只能维护静态的kth查询。
那么对于动态呢？若以同样方式建树，依次枚举之后的链进行修改，很明显不行。
考虑用树状数组。主席树套树状数组。。简直了
通过树状数组的方式->统计当前链要从之前那几条链转移过来，之后见边时同步更新这些链即可。
查询，修改同理。
直接上个板子吧（bzoj1901权限题）

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <vector>
#define N 10005
#define inf 1000000000
using namespace std;
int n,m,a[N];
namespace chairtree
{
    struct tree
    {
        tree* lc;tree* rc;
        int sum;
        tree(){lc=rc=NULL;sum=0;}
        inline void updata(){sum=lc->sum+rc->sum;}
    }*root[N],*null=new tree();
    vector<tree*> v[4];
    tree* newtree()
    {
        tree* o=new tree();
        o->lc=o->rc=null;
        return o;
    }
    inline int low(int x){return x&(-x);}
    void get_ins(int id,int x)
    {
        v[id].clear();
        while(x<=n){v[id].push_back(root[x]);x+=low(x);}
    }
    void get_q(int id,int x)
    {
        v[id].clear();
        while(x>0){v[id].push_back(root[x]);x-=low(x);}
    }
    inline void insert(vector<tree*> o,int l,int r,int k,int h)
    {
        int len=o.size(),mid;
        while(l<r)
        {
            mid=(l+r)>>1;
            for(int i=0;i<len;i++)if(o[i]!=null)o[i]->sum+=h;
            if(k<=mid)
            {
                for(int i=0;i<len;o[i]=o[i]->lc,i++)
                    if(o[i]->lc==null)o[i]->lc=newtree();
                r=mid;
            }
            else
            {
                for(int i=0;i<len;o[i]=o[i]->rc,i++)
                    if(o[i]->rc==null)o[i]->rc=newtree();
                l=mid+1;
            }
        }
        for(int i=0;i<len;i++)
        {
            if(o[i]==null)o[i]=newtree();
            o[i]->sum+=h;
        }
    }
    inline int q(int a,int b,int l,int r,int k)
    {
        get_q(1,a-1);get_q(2,b);
        int mid,len1=v[1].size(),len2=v[2].size();
        while(l<r)
        {
            mid=(l+r)>>1;int t=0;
            for(int i=0;i<len1;i++)if(v[1][i]!=null)t-=v[1][i]->lc->sum;
            for(int i=0;i<len2;i++)if(v[2][i]!=null)t+=v[2][i]->lc->sum;
            if(t>=k)
            {
                for(int i=0;i<len1;i++)v[1][i]=v[1][i]->lc;
                for(int i=0;i<len2;i++)v[2][i]=v[2][i]->lc;
                r=mid;
            }
            else
            {
                for(int i=0;i<len1;i++)v[1][i]=v[1][i]->rc;
                for(int i=0;i<len2;i++)v[2][i]=v[2][i]->rc;
                l=mid+1;k-=t;
            }
        }
        return r;
    }
    inline void change(int l,int k)
    {
        get_ins(1,l);
        insert(v[1],0,inf,a[l],-1);
        insert(v[1],0,inf,k,1);
        a[l]=k;
    }
}
using namespace chairtree;
int main()
{
    scanf("%d%d",&n,&m);null->lc=null->rc=null;
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)root[i]=newtree();
    for(int i=1;i<=n;i++)get_ins(1,i),insert(v[1],0,inf,a[i],1);
    int l,r,k;char s[2];
    while(m--)
    {
        scanf("%s",s);
        if(s[0]=='Q')scanf("%d%d%d",&l,&r,&k),printf("%d\n",q(l,r,0,inf,k));
        else scanf("%d%d",&l,&k),change(l,k);
    }
}

那么同类的问题：历史版本查询，只要把权值线段树改成普通线段树，把每一个位置作为一个“版本”改成真正的版本即可。